Ch ng baươ
ng d ng bi n đ i ứ ụ ế ổ Fourier phân tích tín hi u s và h x lý sệ ố ệ ử ố
Giáo trình lý thuy t m ch đã nghiên c u bi n đ i ế ạ ứ ế ổ Fourier c a tín hi u liên t c. Ch ng ba trình b yủ ệ ụ ươ ầ
bi n đ i ế ổ Fourier c a dãy s và ng d ng c a nó đ phân tích ph c a tín hi u s và đ c tính t n s c a hủ ố ứ ụ ủ ể ổ ủ ệ ố ặ ầ ố ủ ệ
x lý s . ử ố
3.1 bi n đ i ế ổ Fourier c a dãy sủ ố
3.1.1 Bi n đ i ế ổ Fourier thu nậ
3.1.1a Đ nh nghĩa : ịN u dãy x(n) tho mãn đi u ki n :ế ả ề ệ
∞<
∑
∞
−∞=
n
nx )(
[3.1-1]
thì s t n t i phép bi n đ i Fourier nh sau :ẽ ồ ạ ế ổ ư
nj
n
j
enxe
X
.
)()(
ωω
−
∞
−∞=
∑
=
[3.1-2]
Bi n đ i ế ổ Fourier đã chuy n dãy s ể ố x(n) thành hàm ph c ứX(ej
ω
), [3.1-2] là bi u th c bi n đ i ể ứ ế ổ Fourier
thu n và đ c ký hi u nh sau :ậ ượ ệ ư
)()]([
∞
=
j
enxFT
X
[3.1-3]
hay :
)()(
∞
→
j
FT
enx
X
[3.1-4]
(FT là ch vi t t t c a thu t ng ti ng Anh ữ ế ắ ủ ậ ữ ế Fourier Transform).
Ký hi u ệX(ej
ω
) đ phân bi t phép bi n đ i ể ệ ế ổ Fourier c a dãy s ủ ố x(n)
)()]([
∞
=
j
enxFT
X
v i phép bi nớ ế
đ i ổFourier c a hàm liên t c ủ ụ x(t) :
∫
∞
∞−
−
•
==
dtetxtxFT
tj
X
ω
ω
).()()]([
.
Bi u th c bi n đ i ể ứ ế ổ Fourier c a dãy s ủ ố x(n) [3.1-2] là su t phát t bi u th c bi n đ i ấ ừ ể ứ ế ổ Fourier c aủ
hàm liên t c ụx(t), vì khi hàm d i d u tích phân là dãy r i r c thì ph i thay d u tích phân b ng d u t ng .ướ ấ ờ ạ ả ấ ằ ấ ổ
Do tính ch t tu n hoàn c a hàm mũ ấ ầ ủ ej
ω
, nên X(ej
ω
) là hàm tu n hoàn c a bi n ầ ủ ế
ω
v i chu kỳ 2ớπ :
)()()()(
.).2.()2.(
ωωωω
ππ
jnj
n
nkj
n
kj
eenxenxe
XX
===
−
∞
−∞=
+−
∞
−∞=
+
∑∑
Đi u đó có nghĩa là ch c n nghiên c u hàm t n s ề ỉ ầ ứ ầ ố X(ej
ω
) c a các dãy r i r c ủ ờ ạ x(n) v i ớ
ω
∈
(-
π
,
π
)
ho c ặ
ω
∈
( 0 , 2
π
).
S d ng bi n đ i ử ụ ế ổ Fourier cho phép nghiên c u ph c a tín hi u s và đ c tính t n s c a h x lýứ ổ ủ ệ ố ặ ầ ố ủ ệ ử
s . N u ố ế x(n) là tín hi u s thì ệ ố
)()]([
∞
=
j
enxFT
X
là ph c a tín hi u ổ ủ ệ x(n), còn v i ớh(n) là đ c tính xung c aặ ủ
h x lý s thì ệ ử ố
)()]([
∞
=
j
enhFT
H
là đ c tính t n s c a h x lý s . ặ ầ ố ủ ệ ử ố
3.1.1b S t n t i c a bi n đ i ự ồ ạ ủ ế ổ Fourier
Theo đ nh nghĩa, bi n đ i ị ế ổ Fourier thu n [3.1-2] ch t n t i n u dãy ậ ỉ ồ ạ ế x(n) tho mãn đi u ki n khả ề ệ ả
t ng tuy t đ i [3.1-1]. Đi u đó có nghĩa là, n u dãy ổ ệ ố ề ế x(n) tho mãn đi u ki n [3.1-1] thì chu i [3.1-2] s h iả ề ệ ỗ ẽ ộ
t v hàm ụ ề X(ej
ω
), nên x(n) t n t i bi n đ i ồ ạ ế ổ Fourier. Ng c l i, n u dãy ượ ạ ế x(n) không tho mãn đi u ki n [3.1-ả ề ệ
1] thì chu i [3.1-2] s phân kỳ, vì th hàm ỗ ẽ ế X(ej
ω
) không t n t i và ồ ạ x(n) không có bi n đ i ế ổ Fourier.
Các tín hi u s ệ ố x(n) có năng l ng h u h n :ượ ữ ạ
[3.1-5]
luôn th a mãn đi u ki n [3.1-1] , do đó luôn t n t i bi n đ i ỏ ề ệ ồ ạ ế ổ Fourier.
Ví d 3.1ụ : Hãy xét s t n t i và tìm bi n đ i ự ồ ạ ế ổ Fourier c a các dãy sau :ủ
a.
)(nu
b.
)(2nu
n
c.
)(2nu
n−
119
d.
)(n
δ
e.
)( kn −
δ
f.
)(nrectN
Gi i : ảa.
∞==
∑∑
∞
=
∞
−∞=
0
1
)(
nn
nu
Hàm u(n) không tho mãn [3.1-1] nên không t n t i bi n đ i ả ồ ạ ế ổ Fourier.
b.
∞==
∑∑
∞
=
∞
−∞=
0
22
)(
n
n
n
n
nu
Hàm 2nu(n) không tho mãn [3.1-1] nên không t n t i bi n đ i ả ồ ạ ế ổ Fourier.
c.
2
21
1
22
1
0
)(
=
−
==
−
∞
−=
−
∞
−∞=
−
∑∑
n
n
n
n
nu
Hàm 2-nu(n) tho mãn [3.1-1] nên t n t i bi n đ i ả ồ ạ ế ổ Fourier :
( )
∑∑∑
∞
=
−−
∞
=
−−
∞
−∞=
−−−
===
0
1
0
..
.).()](
2222[
n
n
j
n
njn
n
njnn
eeenunu
FT
ωωω
V y :ậ
ωω
jj
n
ee
nuFT −−−
−
−
=
−
=5,01
1
21
1
2[ .
)]( 1
[3.1-6]
d.
1
)(
=
∑
∞
−∞=
n
n
δ
Hàm
δ
(n) tho mãn [3.1-1] nên t n t i bi n đ i ả ồ ạ ế ổ Fourier :
1.1
0.
).()]([
===
−
∞
−∞=
−
∑
ωω
δδ
j
n
nj
eennFT
[3.1-7]
e) Chu i [3.1-1] đ i v i ỗ ố ớ
δ
(n - k) h i t nên nó ộ ụ có bi n đ i ế ổ Fourier :
ωω
δδ
jk
n
nj
eennFT
kk
−
∞
−∞=
−
=−=−
∑
).()]([
[3.1-8]
f.
∞<==
∑∑
−
=
∞
−∞=
N
N
N
nn
nrect
1
0
1
)(
Hàm rect N(n) tho mãn [3.1-1] nên t n t i bi n đ i ả ồ ạ ế ổ Fourier, :
( )
ω
ω
ωω
j
j
n
n
j
n
nj
e
e
eenrectnrectFT
N
N
NN
−
−
−
=
−
∞
−∞=
−
−
−
=== ∑∑
1
1
1
0
).()]([
[3.1-9]
Có th th y r ng, các dãy có đ dài h u h n luôn t n t i bi n đ i ể ấ ằ ộ ữ ạ ồ ạ ế ổ Fourier, còn các dãy có đ dài vôộ
h n s t n t i bi n đ i ạ ẽ ồ ạ ế ổ Fourier n u chu i [3.1-1] c a nó h i t .ế ỗ ủ ộ ụ
3.1.1c Các d ng bi u di n c a hàm ạ ể ễ ủ X(ej
ω
)
Vì X(ej
ω
) là hàm ph c, nên có th bi u di n nó d i các d ng, ph n th c và ph n o, mô đun vàứ ể ể ễ ướ ạ ầ ự ầ ả
argumen, đ l n và pha.ộ ớ
1. D ng ph n th c và ph n oạ ầ ự ầ ả
)()()(
ωω
ω
IR
j
XXX
je
+=
[3.1-10]
Theo công th c ứEuler có :
[ ]
).sin().cos()()()(
.
njnnxenxe
n
nj
n
j
X
ωω
ωω
−==
∑∑
∞
−∞=
−
∞
−∞=
[3.1-11]
Hàm ph n th c : ầ ự
∑
∞
−∞=
==
n
j
R
nnxe
XX
).cos().()](Re[)(
ωω
ω
[3.1-12]
Hàm ph n o : ầ ả
∑
∞
−∞=
−==
n
j
I
nnxe
XX
).sin().()](Im[)(
ωω
ω
[3.1-13]
2. D ng mô đun và argumenạ
)(
.)()(
ωϕωω
jjj
eee
XX
=
[3.1-14]
Mô đun :
)()()(
22
ωω
ω
IR
j
XXX
e
+=
[3.1-15]
Argumen :
[ ]
==
)(
)(
)()(
ω
ω
ωϕ
ω
R
I
j
X
X
X
arctgeArg
[3.1-16]
120
X(ej
ω
) đ c g i là hàm biên đ t n s , nó là hàm ch n và đ i x ng qua tr c tung : ượ ọ ộ ầ ố ẵ ố ứ ụ X(ej
ω
)=X(e-
j
ω
)
ϕ
(
ω
) đ c g i là hàm pha t n s , nóượ ọ ầ ố là hàm l và ph n đ i x ng qua g c to đ : ẻ ả ố ứ ố ạ ộ
ϕ
(
ω
) = - ϕ(-
ω
).
3. D ng đ l n và phaạ ộ ớ
)()(
.)().()(
ωϕωωθωω
jjjjj
eeeee
AAX
==
[3.1-17]
Hàm đ l n ộ ớ A(ej
ω
) có th nh n các giá tr d ng ho c âm, và :ể ậ ị ươ ặ
)()(
ωω
jj
ee
XA
=
[3.1-18]
Còn :
)()()]([
ωϕωθ
ω
=+
j
eArg
A
[3.1-19]
Hàm pha :
)]([)()(
ω
ωϕωθ
j
eArg
A
−=
[3.1-20]
V i ớ
)]([
ω
j
eArg
A
ph thu c vào d u c a hàm ụ ộ ấ ủ
)(
ω
j
e
A
nh sau :ư
<
≥
=
0
00
)(
)(
)]([
ω
ω
ω
π
j
j
j
eKhi
eKhi
eArg
A
A
A
M t cách t ng quát, có th vi t :ộ ổ ể ế
=
=−− )(
)(
)( 1
2
1
2
)]([
ω
ω
ωππ
ω
j
eASign
j
eA
j
eA
j
eArg A
Theo [3.1-20] , có th bi u di n hàm pha ể ể ễ
θ
(
ω
) d i d ng nh sau :ướ ạ ư
−−=
)(
)(
)()(
1
2
ω
ω
ωϕωθ
π
j
eA
j
eA
[3.1-21]
Ví d 3.2ụ : Hãy xác đ nh các hàm ph n th c và ph n o, mô đun và argumen, đ l n và pha c a hàm t n sị ầ ự ầ ả ộ ớ ủ ầ ố
ωω
ω
jj
ee
X
−
=
).cos()(
2
Gi i :ả Theo [3.1-11] có :
)sin().cos()cos().cos()(
22
ωωωω
ω
je
j
X
−=
Hàm ph n th c :ầ ự
)cos().cos()(
2
ωωω
=
R
X
Hàm ph n o :ầ ả
)sin().cos()(
2
ωωω
−=
I
X
Mô đun :
)cos()(cos).(cos)(cos).(cos)(
222
2222
ωωωωω
ω
=+=
j
e
X
Argumen :
ω
ωω
ωω
ωϕ
−=
−=
)cos().cos(
)sin().cos(
)(
2
2
arctg
Hàm đ l n : ộ ớ
)cos()(
2
ω
ω
=
j
e
A
Hàm pha :
.
)cos(
)cos(
)( 2
2
1
2
−−−=
ω
ω
ωωθ π
3.1.1d Quan h gi a bi n đ i ệ ữ ế ổ Fourier và bi n đ i ế ổ Z
Theo bi u th c đ nh nghĩa [2.1-1] c a bi n đ i Z có :ể ứ ị ủ ế ổ
∑
∞
−∞=
−
==
n
n
znxznxZT
X
)()()]([(
, v i ớ
+−
<<
xx
RRX
zzRC ||:)]([
Bi u di n s ph c ể ễ ố ứ z theo t a đ c c : ọ ộ ự z = r.ej
ω
v i |ớz|= r và arg [z] =
ω
V y :ậ
∑∑
∞
−∞=
−−
∞
−∞=
−
===
n
njn
n
njj
ernxernxerz
XX
.
.).().).(().()(
ωωω
Khi |z|= r = 1 thì z = ej
ω
, nên nh n đ c :ậ ượ
∑
∞
−∞=
−
==
=
n
njj
j
enxe
ez
z
XX
.
).()()(
ωω
ω
[3.1-22]
Theo [3.1-22] thì bi n đ i ế ổ Fourier chính là bi n đ i ế ổ Z khi z n m trên vòng tròn đ n v ằ ơ ị | z | = 1 , nghĩa
là bi n đ i ế ổ Fourier là m t tr ng h p riêng c a bi n đ i ộ ườ ợ ủ ế ổ Z.
121
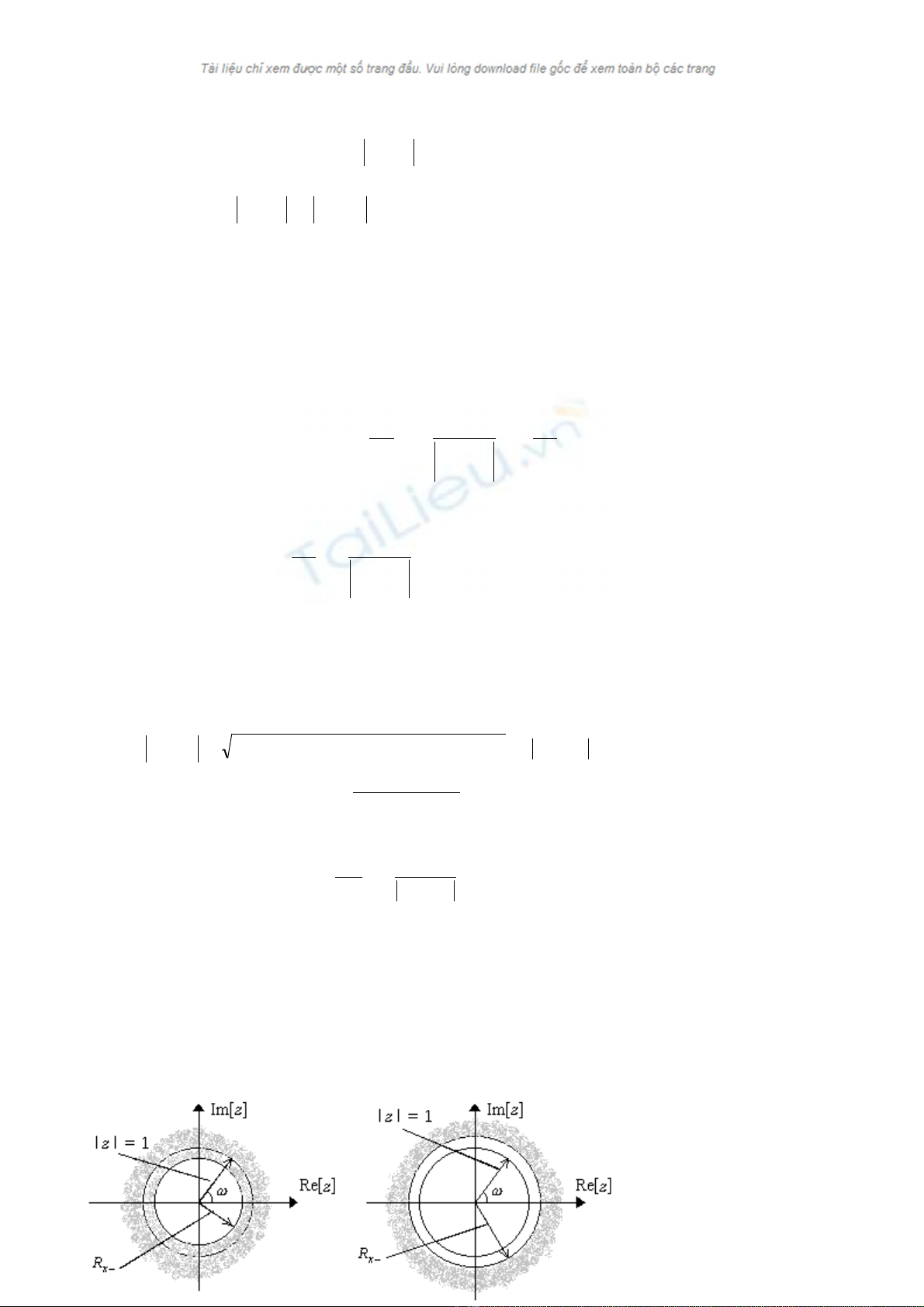
a.
1
|| =<
−
z
x
R
, t n t iồ ạ FT b.
1
|| =≥
−
z
x
R
, không t n t iồ ạ FT
Hình 3.1 : Quan h gi a ệ ữ bi n đ i ế ổ Fourier và bi n đ iế ổ Z
T hình 3.1a th y r ng, n u hàm ừ ấ ằ ế X(z) h i t trên vòng tròn đ n v ộ ụ ơ ị | z | = 1 thì ch c ch n dãy ắ ắ x(n) t nồ
t i bi n đ i ạ ế ổ Fourier, và ng c l i. T hình 3.1b, n u hàm ượ ạ ừ ế X(z) không h i t trên vòng tròn đ n v ộ ụ ơ ị |z| = 1,
thì dãy x(n) s không t n t i bi n đ i ẽ ồ ạ ế ổ Fourier, và ng c l i. ượ ạ
Hàm b c thang đ n v ậ ơ ị u(n) là m t ví d : Hàm ộ ụ
)()]([( znuZT
U
=
có
1
||:)]([ >zzRC
U
, do U(z) không
h i t trên vòng tròn đ n v ộ ụ ơ ị | z | = 1 nên u(n) không có bi n đ i ế ổ Fourier, câu a ví d 3.1 đã ch ng minh đi uụ ứ ề
đó.
3.1.2 Bi n đ i ế ổ Fourier ng cượ
Bi n đ i ế ổ Fourier ng c cho phép tìm dãy ượ x(n) t hàm nh ừ ả X(ej
ω
). Đ tìm bi u th c c a phép bi nể ể ứ ủ ế
đ i ổFourier ng c, xu t phát t bi u th c ượ ấ ừ ể ứ Fourier thu n [3.1-2] :ậ
nj
n
j
enxe
X
.
)()(
ωω
−
∞
−∞=
∑
=
[3.1-23]
Nhân c hai v c a [3.1-23] v i ả ế ủ ớ ej
ω
.m r i l y tích phân trong kho ng ồ ấ ả (-
π
,
π
) , nh n đ c :ậ ượ
∫ ∫ ∫
∑∑
− − −
−
∞
−∞=
∞
−∞=
−
==
π
π
π
π
π
π
ωωωωω
ωωω
denxdeenxdee
nmj
nn
mjnjmjj
X
).(...
.)(.).().(
Vì :
≠
=
=
∫
−
−
nmkhi
nmkhi
de
nmj
0
2
)(
π
ω
π
π
ω
Nên :
)(.).( 2nxdee njj
X
π
π
π
ωω ω
=
∫
−
T đó suy ra bi u th c c a phép bi n đ i ừ ể ứ ủ ế ổ Fourier ng c :ượ
∫
−
=
π
π
ωω
ω
π
deenx
njj
X
.
).()(
2
1
[3.1-24]
Phép bi n đ i ế ổ Fourier ng c đ c ký hi u nh sau :ượ ượ ệ ư
)()](
[
nxe
j
XIFT
=
ω
[3.1-25]
Hay :
)()( nxe
IFT
j
X
→
ω
[3.1-26]
(IFT là ch vi t t t c a thu t ng ti ng Anh ữ ế ắ ủ ậ ữ ế Inverse Fourier Transform).
Bi u th c bi n đ i ể ứ ế ổ Fourier thu n [3.1-23] và bi u th c bi n đ i ậ ể ứ ế ổ Fourier ng c [3.1-24] h p thànhượ ợ
c p bi n đ i ặ ế ổ Fourier c a dãy s ủ ố x(n).
Ví d 3.3ụ : Hãy tìm tín hi u s ệ ố x(n) có hàm ph là ổ
ωω
ω
2
).cos()(
jj
ee
X
−
=
.
Gi i :ả Theo [3.1-24] có :
∫
−
−
=
π
π
ωω
ωω
π
deenx
njj .2
.).cos()(
2
1
[ ]
∫ ∫
− −
−−−
−
+=
+
=
π
π
π
π
ωωωω
ωω
ω
π
ω
π
deedee
ee
nx
njnjnjj
jj
)3()1(.2
4
1
22
1
..
)(
)(
−
+
−
=
−
−
−
−
π
π
ω
π
π
ω
π
|
)(
1
|
)(
1
)(
)3()1(
314
1
njnj
e
nj
e
nj
nx
122
−
−
+
−
−
=
−−−−−−
)()(
)(
314
1
)3()3()1()1(
nj
ee
nj
ee
nx
njnjnjnj
ππππ
π
232
1
212
1
][
.
)(
][
.
)(
)(
)3()3()1()1(
j
ee
nj
ee
n
nx
njnjnjnj
ππππ
ππ
−−−−−−
−
−
+
−
−
=
π
π
π
π
)(
])sin[(
)(
])sin[(
)(
3
3
2
1
1
1
2
1
−
−
+
−
−
=n
n
n
n
nx
Vì :
)(
)(
])sin[(
)(
])sin[(
0
1k
k
k
k
k
k
k
n
n
n
nkhi
nkhi
n
n−=
−
−
⇒
≠
=
=
−
−
δ
π
π
π
π
Nên :
)()()(
3
2
1
1
2
1
−+−= nnnx
δδ
Vì
ω
ω
j
j
ez
ze
XX
=
=
)()(
, nên đ l p b ng bi n đ i ể ậ ả ế ổ Fourier ch c n s d ng b ng bi n đ i ỉ ầ ử ụ ả ế ổ z khi thay
z = ej
ω
, và đ tìm bi n đ i ể ế ổ Fourier ng c, ngoài cách tính tr c ti p tích phân [3.1-24], cũng có th s d ngượ ự ế ể ử ụ
các ph ng pháp gi ng nh tìm bi n đ i ươ ố ư ế ổ Z ng c.ượ
3.1.3 Các tính ch t c a bi n đ i ấ ủ ế ổ Fourier
Do bi n đ i ế ổ Fourier là m t tr ng h p riêng c a bi n đ i ộ ườ ợ ủ ế ổ Z nên, bi n đ i ế ổ Fourier cũng có các tính
ch t gi ng nh bi n đ i ấ ố ư ế ổ Z. D i đây trình b y các tính ch t th ng đ c s d ng khi phân tích ph tínướ ầ ấ ườ ượ ử ụ ổ
hi u s và đ c tính t n s c a h x lý s .ệ ố ặ ầ ố ủ ệ ử ố
3.1.3a Tính ch t tuy n tính : ấ ế Hàm t n s c a t h p tuy n tính các dãy b ng t h p tuy n tính các hàmầ ố ủ ổ ợ ế ằ ổ ợ ế
t n s thành ph n.ầ ố ầ
N u : ế
)()]([
ω
j
ii enxFT X=
Thì :
)(.)(.)()(
ωω
j
i
i
i
i
ii
jeAnxAnyFTe XY ∑∑ =
==
[3.1-27]
Trong đó các h s ệ ố Ai là các h ng s .ằ ố
Ch ng minh : ứTheo bi u th c bi n đ i ể ứ ế ổ Fourier thu n ậ[3.1-2] có :
∑∑∑ ∑∑ ∞
−∞=
−
∞
−∞=
−==
=
n
nj
i
i
i
n i
nj
ii
i
ii
jenxAenxAnxAFTeY.. ).().(.)(.)(
ωωω
Vì
)()]([).( .
ωω
j
ii
n
nj
ienxFTenx X==
∑
∞
−∞=
−
, nên nh n đ c [3.1-27].ậ ượ
Ví d 3.4ụ : Hãy tìm hàm ph c a tín hi u s ổ ủ ệ ố
)()()(
3
2
1
1
2
1
−+−= nnnx
δδ
Gi i :ả Theo tính ch t tuy n tính c a bi n đ i ấ ế ủ ế ổ Fourier có :
ωωωωω δδ
3..
2
1
2
1
3
2
1
1
2
1).().()( jj
n
nj
n
njj eeeneneX−−
∞
−∞=
−
∞
−∞=
−+=−+−= ∑∑
ωω
ωω
ωω
22 ).cos(.
)(
)( 2
jj
jj
jee
ee
eX−−
−=
+
=
Các ví d 3.3 và 3.4 là hai bài toán ng c nhau, v i k t qu là đ ng nh t.ụ ượ ớ ế ả ồ ấ
3.1.3b Tính ch t tr : ấ ễ Khi d ch tr dãy x(n) đi kị ễ m u thì hàm biên đ t n sẫ ộ ầ ốX(ej
ω
) không thay đ i, ch cóổ ỉ
hàm pha t n s ầ ố ϕ(
ω
) b d ch đi l ng kị ị ượ
ω
.
N u : ế
)(
.)()()]([
ωϕωω
jjj eeenxFT XX ==
Thì :
[ ]
])([
.)()()(
ωωϕωωω
kjjjjk
eeeenxFT
XXk
−−
==−
[3.1-28]
N u ếk > 0 là x(n) b gi tr ị ữ ễ k m u, ẫn u ếk < 0 là x(n) đ c đ y s m ượ ẩ ớ k m u.ẫ
Ch ng minh : ứTheo bi u th c bi n đ i ể ứ ế ổ Fourier thu n ậ[3.1-2] có :
[ ]
)().().()( .).(..
ωωωωω
jkj
n
knjkj
n
nj eeeknxeeknxknxFT X
−
∞
−∞=
−−−
∞
−∞=
−=−=−=− ∑∑
Ví d 3.5 :ụ Hãy tìm :
)]([)( 2nrectFTe N
nj
X−
=
ω
Gi i : ảCó
)()()( 222 Nnununrect nnn
N−−= −−−
Nên :
)](.[)]([)( )(
222 NX nuFTnuFTe NN nnj −−= −−−−
ω
123