http://truongthanh85.violet.vn. ĐT: 0974.810.957
I. TÓM T T LÍ THUY TẮ Ế
1.Khái ni m con l c đ n.ệ ắ ơ
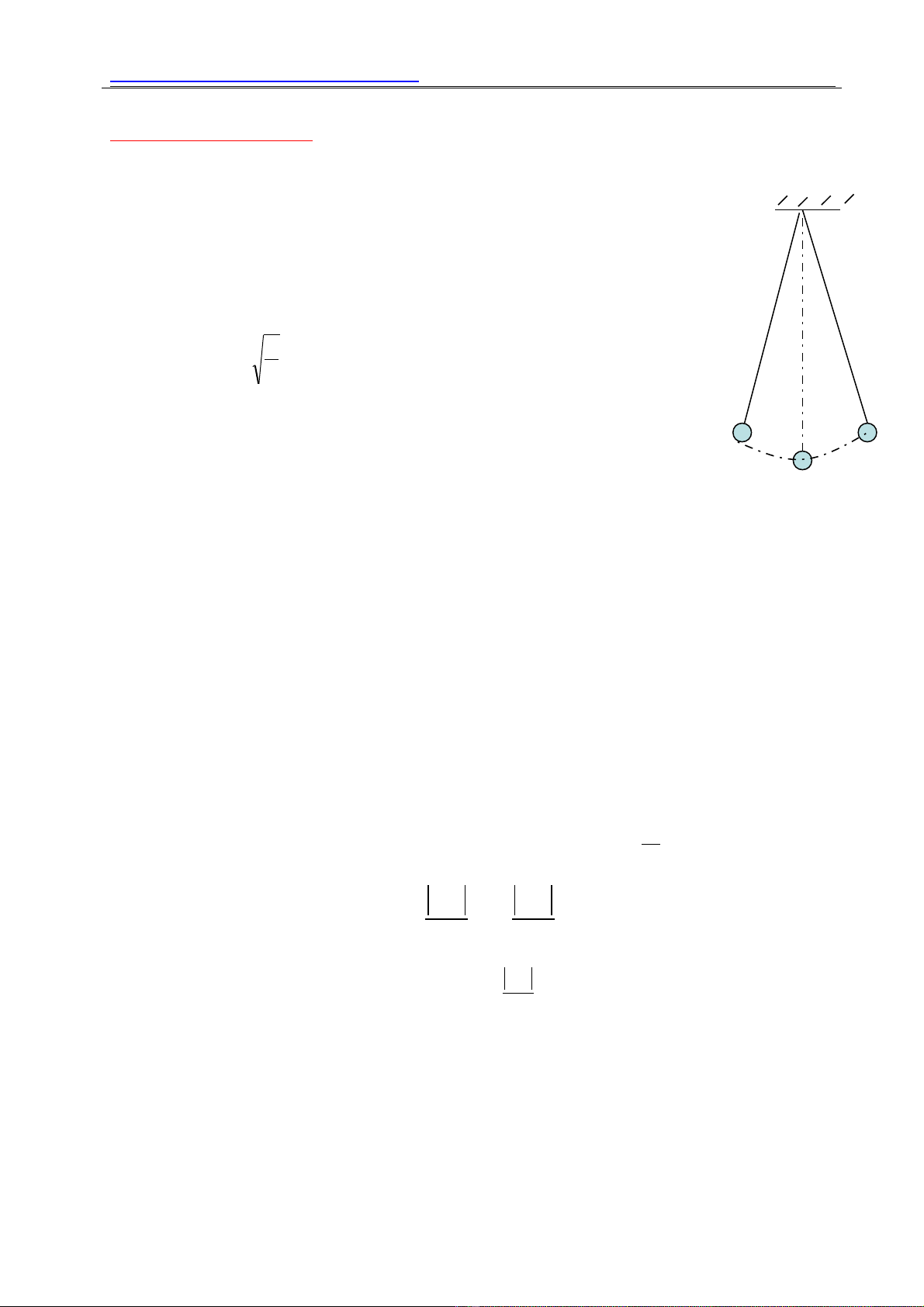
- Con l c đ n g m m t v t nh , kh i l ng m, treo đ u m t s i dây m m khôngắ ơ ồ ộ ậ ỏ ố ượ ở ầ ộ ợ ề
dãn, kh i l ng không đáng k , dài ố ượ ể l.
- Trong h quy chi u quán tính, v trí cân b ng c a con l c đ n là v trí dây treo có ph ngệ ế ị ằ ủ ắ ơ ị ươ
th ng đ ng, v t n ng v trí th p nh t.ẳ ứ ậ ặ ở ị ấ ấ
- Khi dao đ ng c a con l c đ n v i góc l ch nh ( sinαộ ủ ắ ơ ớ ệ ỏ
α
≈
(rad)), con l c dao đ ng đi u hoàắ ộ ề
v i chu kỳ:ớ
g
l
T
π
2=
Trong đó:l là chi u dài c a con l c (đ n v là mét); g là gia t c tr ng tr ng t i v trí đ t conề ủ ắ ơ ị ố ọ ườ ạ ị ặ
l c ( đ n v m/sắ ơ ị 2).
2. Con l c đ ng h .ắ ồ ồ
- Đ ng h qu l c có con l c làm b ng thanh kim lo i m nh và dao đ ng c a con l cồ ồ ả ắ ắ ằ ạ ả ộ ủ ắ
có th coi nh dao đ ng đi u hoà c a con l c đ n.ể ư ộ ề ủ ắ ơ
- Chu kỳ ch y đúng c a đ ng h là T (th ng T =2s); trong m t s tr ng h p doạ ủ ồ ồ ườ ộ ố ườ ợ
nhi t đ môi tr ng thay đ i và v trí đ t con l c thay đ i nên đ ng h ch y sai. G i chu kỳệ ộ ườ ổ ị ặ ắ ổ ồ ồ ạ ọ
ch y sai c a đ ng h là Tạ ủ ồ ồ 2 (còn chu kỳ ch y đúng T =Tạ1) và đ bi n thiên chu kỳ là ộ ế
∆
T = T2
– T1. N u:ế
+
∆
T> 0: T2 > T1: Chu kỳ tăng, đ ng h ch y ch m.ồ ồ ạ ậ
+
∆
T< 0: T2 < T1 :Chu kỳ gi m, đ ng h ch y nhanh.ả ồ ồ ạ
+
∆
T= 0. Chu kỳ không đ i, con l c ch y đúng.ổ ắ ạ
- Th i gian con l c đ ng h ch y sai sau kho ng th i gianờ ắ ồ ồ ạ ả ờ
τ
:
+ Th i gian bi u ki n con l c ch y sai ch là: ờ ể ế ắ ạ ỉ
1
'nT=
τ
.
V i n là s chu kỳ con l c ch y sai ớ ố ắ ạ T2 trong kho ng th i gianả ờ
τ
:
2
T
n
τ
=
.
+ Th i gian ch y sai: ờ ạ
12
'
T
T
T
T
∆
≈
∆
=−=
ττττθ
N u Tế2 thay đ i không đáng k so v i Tổ ể ớ 1 thì:
1
T
T∆
≈
τθ
II. CÁC D NG BÀI TOÁN VÀ PH NG PHÁP GI IẠ ƯƠ Ả
D ng 1: Chu kỳ con l c đ n thay đ i theo chi u dài l.ạ ắ ơ ổ ề
1.1/ Con l c đ n có chi u dài c t ghép.ắ ơ ề ắ
1.2/ Chu kỳ c a con l c v ng đinhủ ắ ướ .
1.3/ Chi u dài con l c đ n thay đ i theo nhi t đ môi tr ng.ề ắ ơ ổ ệ ộ ườ
1
α
B
l
A
m
http://truongthanh85.violet.vn. ĐT: 0974.810.957
1.4/ Chi u dài con l c thay đ i do c t (ho c thêm) m t l ng r t nh ề ắ ổ ắ ặ ộ ượ ấ ỏ
D ng 2: Chu kỳ con l c ạ ắ đ n thay đ i theo gia t c tr ng tr ng g.ơ ổ ố ọ ườ
2.1/ Gia t c g thay đ i theo đ cao.ố ổ ộ
2.2/ Gia t c trong tr ng g thay đ i theo đ sâu.ố ườ ổ ộ
2.3/ Thay đ i v trí đ a lí đ t con l c.ổ ị ị ặ ắ
D ngạ 3: Thay đ i đ ng th i c chi u dài l và gia t c tr ng tr ng g.ổ ồ ờ ả ề ố ọ ườ
3.1/ Thay đ i nhi t đ môi tr ng và thay đ i gia t c tr ng tr ng g.ổ ệ ộ ườ ổ ố ọ ườ
3.2/ Chi u dài con l c thay đ i do c t (ho c thêm) m t l ng ề ắ ổ ắ ặ ộ ượ
và thay
đ i gia t c g.ổ ố
D ng 4: Chu kỳ con l c đ n thay đ i khi có thêm l c lạ ắ ơ ổ ự ạ.
4.1/ L c l là l c đ y Acsimet.ự ạ ự ẩ
4.2/ L c là l c đi n.ự ự ệ
4.3/ L c là là l c quán tính.ự ự
S d ng m t s công th c g n đúng:ử ụ ộ ố ứ ầ
N uế
ε
r t nh so v i 1 thì: ấ ỏ ớ
;1)1(
εε
n
n+≈+
;1)1(
εε
n
n−≈−
2121 1)1)(1(
εεεε
±±≈±±
D ng 1: Chu kỳ con l c đ n thay đ i theo chi u dài lạ ắ ơ ổ ề
1.1/ Con l c đ n có chi u dài c t ghép.ắ ơ ề ắ
* Ph ng pháp:ươ
- Vi t công th c tính chu kỳ T theo chi u dài ế ứ ề l1;l2:( gi s ả ử l2 >l1).
g
l
T1
12
π
=
g
l
T
2
2
2
π
=
- Chu kỳ T c a con l c chi u dài ủ ắ ề l là
g
l
T
π
2=
l = l1+l2 Bi n đ i ta đ c : ế ổ ượ
2
2
2
1TTT +=
l = l1- l2 T ng t : ươ ự
2
2
2
1TTT −=
* Ví d :ụ
Ví d 1:ụ Con l c đ n chi u dài ắ ơ ề l1 dao đ ng đi u hoà t i m t n i v i chu kỳ ộ ề ạ ộ ơ ớ T1 = 1,5s. Con
l c đ n chi u dài ắ ơ ề l2 cũng dao đ ng đi u hoà t i n i đó v i chu kỳ ộ ề ạ ơ ớ T2 =0,9s. Tính chu kỳ c aủ
con l c chi u dài ắ ề l dao đ ng đi u hoà n i trên v i:ộ ề ở ơ ớ
l = l1+l2 và l = l1- l2
H ng d n:ướ ẫ
2
http://truongthanh85.violet.vn. ĐT: 0974.810.957
-V iớ l = l1+l2 S d ng công th cử ụ ứ
2
2
2
1TTT +=
Thay s :ố
sT 75,19,05,1 22 =+=
-Viớ l = l1- l2 S d ng công th cử ụ ứ
2
2
2
1TTT −=
Thay s :ố
sT 2,19,05,1 22 =−=
Ví d 2:ụ
M t con l c đ n có dây treo chi u dài ộ ắ ơ ề l. Ng i ta thay đ i đ dài c a nó t i giá tr ườ ổ ộ ủ ớ ị l’ sao cho
chu kỳ dao đ ng m i ch b ng 90% chu kỳ dao đ ng ban đ u. H i chi u dài ộ ớ ỉ ằ ộ ầ ỏ ề l’ b ng bao nhiêuằ
l n chi u dàiầ ề l ?
H ng d n: ướ ẫ Chu kỳ con l c chi u dài ắ ề l và l’ l n l t là:ầ ượ
g
l
T
π
2
1=
và
g
l
T
'
22
π
=
T s : ỷ ố
9,0%90
'
1
2=== l
l
T
T
ll 81,0
'=⇒
Ví d 3:ụ
T i m t n i trên m t đ t m t con l c đ n dao đ ng đi u hoà.Trong kho ng th i gian ạ ộ ơ ặ ấ ộ ắ ơ ộ ề ả ờ
,
con l c th c hi n 60 dao đ ng toàn ph n; thay đ i chi u dài con l c m t đo n 44 cm thì cũngắ ự ệ ộ ầ ổ ề ắ ộ ạ
trong kho ng th i gian ả ờ
y, nó th c hi n 50 dao đ ng toàn ph n. Xác đ nh chi u dài banấ ự ệ ộ ầ ị ề
đ u c a con l c ?ầ ủ ắ
H ng d n:ướ ẫ
G i chu kỳ con l c chi u dài lọ ắ ề 1, l2 là T1;T2
Xét trong kho ng th i gian ả ờ
nh nhau thì: 60Tư1 = 50T2
5
6
1
2
1
2==⇒ l
l
T
T
25
36
1
2=⇒ l
l
12 25
36 ll =⇒
và l2 = l1 +44.
Gi i h đ c: l = 100 cm.ả ệ ượ
1.2/Chu kỳ c a con l c v ng đinhủ ắ ướ .
*Ph ng pháp:ươ
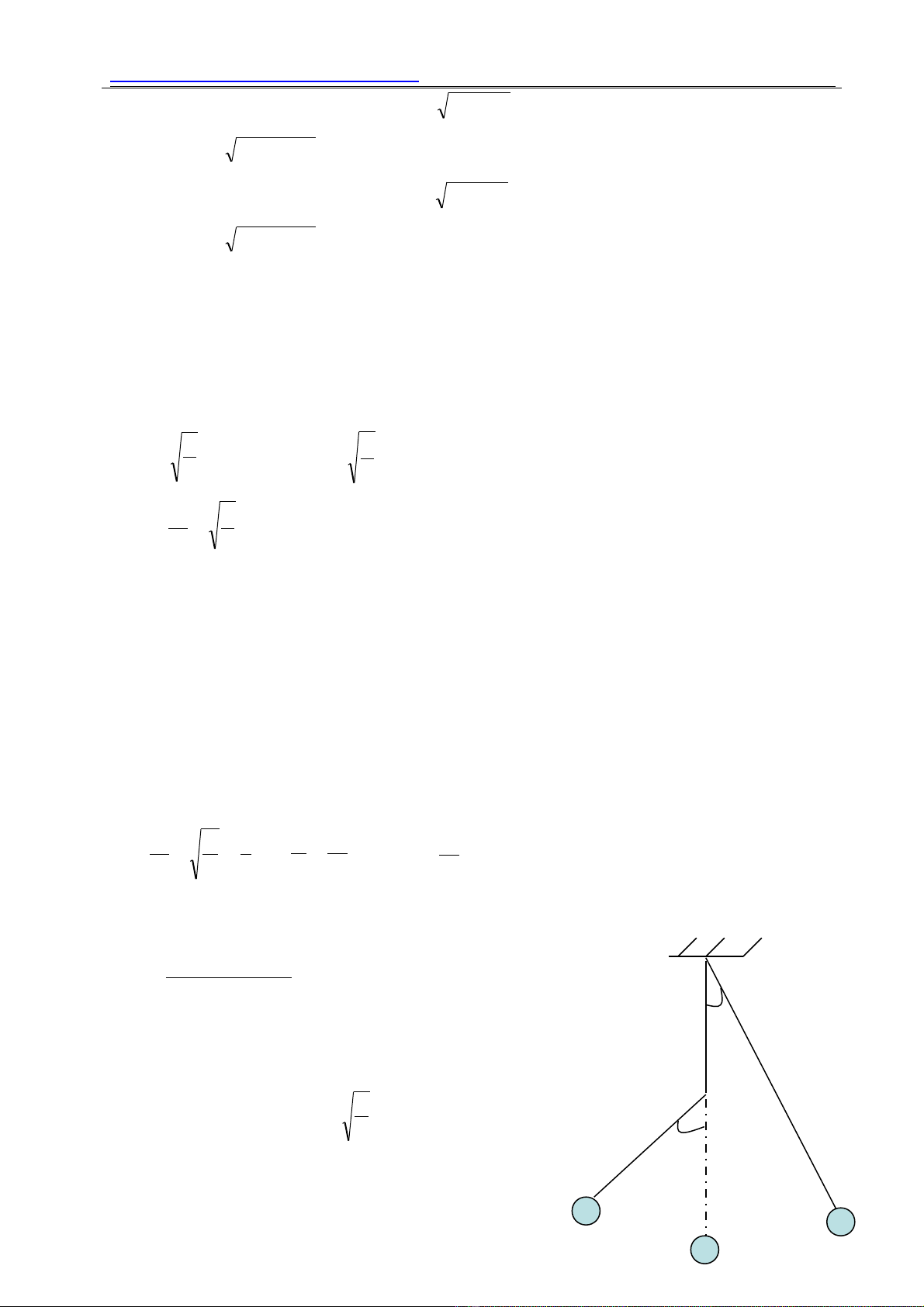
M t dao đ ng toàn ph n c a con l c bộ ộ ầ ủ ắ ị
v ng đinh g m 2 giai đo n:ướ ồ ạ
+ Giai đo n đ u con l c dao đ ng v iạ ầ ắ ộ ớ
chi u dài ềl và chu kỳ
g
l
T
π
2
1=
.
+ Giai đo n còn l i nó dao đ ng v iạ ạ ộ ớ
chi u dài ềl’ (đi m treo con l c là v trí đinh)ể ắ ị
3
α1
l
I
α2
http://truongthanh85.violet.vn. ĐT: 0974.810.957
và chu kỳ
g
l
T
'
22
π
=
.
Chu kỳ c a con l c là: ủ ắ
)(
2
1
2
1
2
1
2121 TTTTT +=+=
* Ví d :ụ
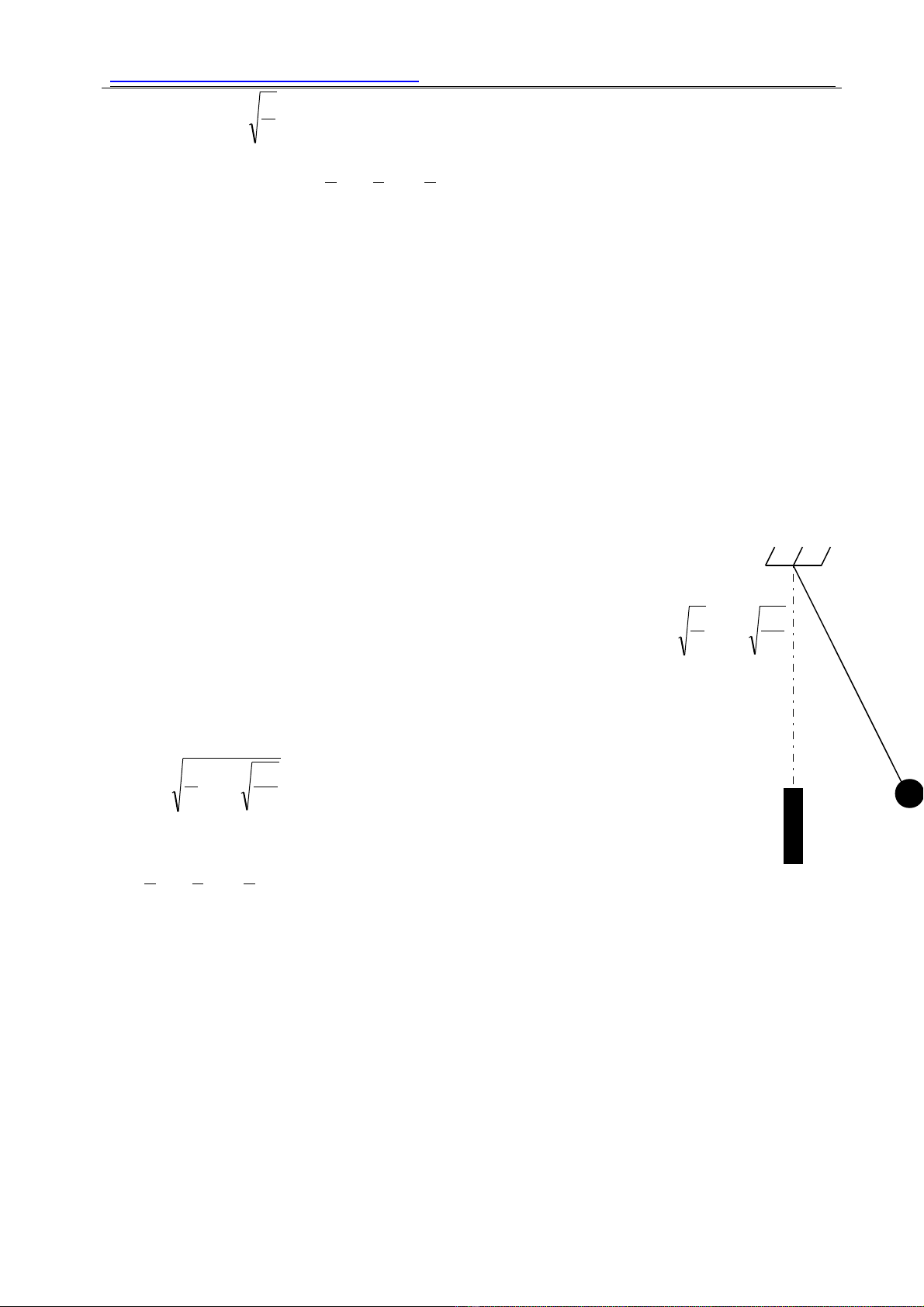
M t con l c đ n g m m t qu c u nh kh i l ng m làm b ng thép treo vào đ u m t s iộ ắ ơ ồ ộ ả ầ ỏ ố ượ ằ ầ ộ ợ
dây m m có kh i l ng không đáng k dài l = 1 m.Phía d i đi m treo Q theo ph ng th ngề ố ượ ể ướ ể ươ ẳ
đ ng c a s i dây có m t chi c đinh đ c đóng vào đi m Oứ ủ ợ ộ ế ượ ể ’ cách Q m t đo n Oộ ạ ’Q = 50 cm
sao cho con l c b v p ph i đinh trong quá trình dao đ ng đi u hoà.ắ ị ấ ả ộ ề
a/ Xác đ nh chu kỳ dao đ ng c a qu c u? cho gia t c g = 9,8 m/sị ộ ủ ả ầ ố 2
b/N u không đóng đinh vào Oế’ mà đ t t i v trí cân b ng O m t t m thép đ c gi c đ nhặ ạ ị ằ ộ ấ ượ ữ ố ị
thì hi n t ng x y ra nh th nào? (Coi r ng va ch m c a qu c u vào v t c n là hoàn toànệ ượ ả ư ế ằ ạ ủ ả ầ ậ ả
đàn h i)ồ
H ng d n:ướ ẫ
a/ Trong quá trình dao đ ng con l c b v ng vào đinh Oộ ắ ị ướ ’ n m trên ph ng th ng đ ng c aằ ươ ẳ ứ ủ
dây treo nên m i dao đ ng toàn ph n c a con l c g m 2 giai đo nỗ ộ ầ ủ ắ ồ ạ
+ Giai đo n đ u con l c dao đ ng v i chi u dài ạ ầ ắ ộ ớ ề l =1m và chu kỳ
s
g
l
T2
8,9
1
22
1===
ππ
.
+ Giai đo n còn l i nó dao đ ng v i chi u dài ạ ạ ộ ớ ề l’ = OO’ =0,5m và chu kỳ
s
g
l
T4,1
8,9
5,0
22
'
2===
ππ
.
Chu kỳ c a con l c b v ng đinh là:ủ ắ ị ướ
)(
2
1
2
1
2
1
2121 TTTTT +=+=
= 1/2 (2+1,4) = 1,7 s
b/ T m thép đ t tai VTCB O: Vì va ch m gi a qu c u và t m thép là hoàn toàn đàn h i nênấ ặ ạ ữ ả ầ ấ ồ
khi qu c u va ch m vào t m thép nó s b t ng c l i v i v n t c có cùng đ l n ngayả ầ ạ ấ ẽ ậ ượ ạ ớ ậ ố ộ ớ
tr c lúc va ch m và v t l i lên đúng v trí cao nh t A ( Vì c năng b o toàn).ướ ạ ậ ạ ị ấ ơ ả
V y con l c ch dao đ ng trên cung OA nên chu kỳ dao đ ngậ ắ ỉ ộ ộ
là:
T = 1/2T1 = 1 s.
*Ví d 1:ụ
M t đ ng h qu l c đ m giây có chu kỳ ộ ồ ồ ả ắ ế T = 2s. Qu l c đ c coi nh m t con l c đ n v iả ắ ượ ư ộ ắ ơ ớ
dây treo và v t n ng làm b ng đ ng có h s n dàiậ ặ ằ ồ ệ ố ở
4
O
A
http://truongthanh85.violet.vn. ĐT: 0974.810.957
α
= 17.10-6K-1. Gi s đ ng h ch y đúng chân không, nhi t đ 20ả ử ồ ồ ạ ở ệ ộ 0c.
Tính chu kỳ c a con l c trong chân không 30ủ ắ ở 0c ? 30ở0c đ ng h ch y nhanh hay ch m?ồ ồ ạ ậ
M i ngày ch y sai bao nhiêu?ỗ ạ
H ng d n:ướ ẫ + S d ng công th c: ử ụ ứ
12 )
2
1
1( TtT ∆+=
α
Thay s : ố
2)).2030(10.17
2
1
1( 6
2−+= −
T
= 2,00017 s
+ Chu kỳ T2>T nên đ ng h ch y ch m.ồ ồ ạ ậ
Th i gian ch y ch m trong m t ngày đêm : ờ ạ ậ ộ
τ
= 24.60.60 s là:
t
T
T∆=
∆
=
αττθ
2
1
1
= 24.3600.1/2.17.10-6 .10 = 7,34 s.
Ví d 2ụ:
M t đ ng h qu l c ch y đúng gi vào mùa nóng khi nhi t đ trung bình là 32ộ ồ ồ ả ắ ạ ờ ệ ộ 0c, con l c cóắ
th xem là con l c đ n. H s n dài c a dây treo con l cể ắ ơ ệ ố ở ủ ắ
α
= 2.10-5K-1. Vào mùa l nh nhi t đ trung bình là 17ạ ệ ộ 0c h i con l c s ch y nh th nào?ỏ ắ ẽ ạ ư ế
M t tu n nó chay sai bao nhiêu?ộ ầ
H ng d nướ ẫ : Do nhi t đ vào mùa đông gi m nên chu kỳ con l c gi m, đ ng h ch y nhanh.ệ ộ ả ắ ả ồ ồ ạ
M t tu n :ộ ầ
τ
= 7.24.60.60 s đ ng h ch y nhanh m t th i gian:ồ ồ ạ ộ ờ
t
T
T∆=
∆
=
αττθ
2
1
1
= 7.24.3600.1/2.2.10-5 .15 = 90,72 s.
Ví d 3ụ: Con l c đ ng h có dây treo làm b ng thanh kim lo i m nh. khi nhi t đ môiắ ồ ồ ằ ạ ả ệ ộ
tr ng tăng thêm 10ườ 0c thì trong 12 gi con l c ch y ch m 30s. N u mu n con l c ch y m iờ ắ ạ ậ ế ố ắ ạ ỗ
ngày ch ch m 45s thì nhi t đ môi tr ng ph i tăng lên bao nhiêu? Coi gia t c tr ng tr ngỉ ậ ệ ộ ườ ả ố ọ ườ
không thay đ i.ổ
H ng d n:ướ ẫ
V n d ng công th c: ậ ụ ứ
t
T
T∆=
∆
=
αττθ
2
1
1
Khi nhi t đ tăng thêm30ệ ộ 0c thì m i ngày s ch y ch m: ỗ ẽ ạ ậ
1 1
160
2t s
θ α
= ∆ =
;
N u con l c ch y ch m m i ngày 45s thì nhi t đ tăng lên ế ắ ạ ậ ỗ ệ ộ
2
t∆
tho mãn:ả
0
2 2 2 1
145 3 / 4 11, 25
2t s t t c
θ α
= ∆ = ∆ = ∆ =�
1.3.Chi u dài con l c đ n thay đ i theo nhi t đ môi tr ng.ề ắ ơ ổ ệ ộ ườ
5
O