Chuyên đ 2: DAO Đ NG C H Cề Ộ Ơ Ọ
A. TÓM T T LÝ THUY TẮ Ế
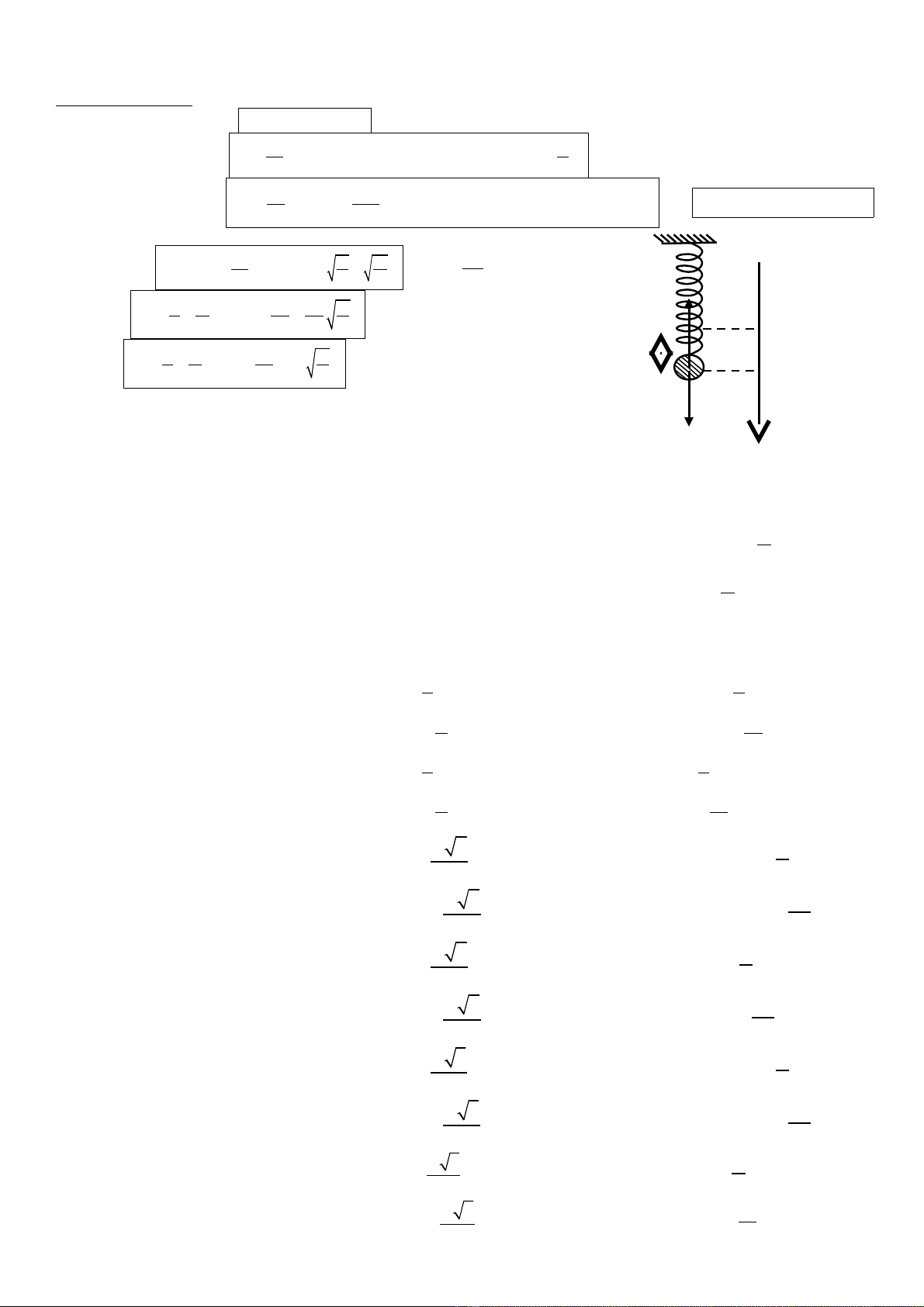
I. CON L C LÒ XOẮ
1. Ph ng trình dao đ ngươ ộ :
cos( )x A t
ω ϕ
= +
2. Ph ng trình v n t c:ươ ậ ố
'; sin( ) cos( )
2
dx
v x v A t A t
dt
π
ω ω ϕ ω ω ϕ
= = =− + = + +
3. Ph ng trình gia t c:ươ ố
22 2
2
'; ''; cos( );
dv d x
a v a x a A t a x
dt dt
ω ω ϕ ω
= = = = =− + =−
Hay
2
cos( )a A t
ω ω ϕ π
= + ±
4. T n s góc, chu kì, t n s và pha dao đ ng, pha ban đ u:ầ ố ầ ố ộ ầ
a. T n s góc:ầ ố
2
2 ( / ); k g
f rad s
T m l
π
ω π ω
= = = = ∆
;
( )
mg
l m
k
∆ =
b. T n s :ầ ố
1 1
( ); 2 2
N k
f Hz f
T t m
ω
π π
= = = =
c. Chu kì:
1 2
( ); 2
t m
T s T
f N k
ππ
ω
= = = =
d. Pha dao đ ng:ộ
( )t
ω ϕ
+
e. Pha ban đ u:ầ
ϕ
Chú ý: Tìm
ϕ
, ta d a vào h ph ng trìnhự ệ ươ
0
0
cos
sin
x A
v A
ϕ
ω ϕ
=
= −
lúc
0
0t=
M T S TR NG H P TH NG G PỘ Ố ƯỜ Ợ ƯỜ Ặ
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua VTCB ậ
0
0x=
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
2
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua VTCB ậ
0
0x=
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
2
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua biên d ngậ ươ
0
x A=
: Pha ban đ u ầ
0
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua biên âmậ
0
x A= −
: Pha ban đ u ầ
ϕ π
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x=
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
3
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x= −
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
π
ϕ
= −
2
3
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x=
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
3
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
A
x
= −
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
2
3
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x=
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
4
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x= −
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
π
ϕ
= − 3
4
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x=
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
4
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
2
2
A
x= −
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
3
4
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x=
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
6
π
ϕ
= −
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x= −
theo chi u d ng ề ươ
0
0v>
: Pha ban đ u ầ
π
ϕ
= − 5
6
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x=
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
6
π
ϕ
=
♦Ch n g c th i gian ọ ố ờ
0
0t=
là lúc v t qua v trí ậ ị
0
3
2
A
x
= −
theo chi u âm ề
0
0v<
: Pha ban đ u ầ
5
6
π
ϕ
=
1
l
∆
x
O
K
m
P

-
3
-1
-
3
/3
(Ñieåm goác)
t
t'
y
y'
x
x'
u
u'
-
3
-1
-
3
/3
1
1
-1
-1
-
π
/2
π
5
π
/6
3
π
/4
2
π
/3
-
π
/6
-
π
/4
-
π
/3
-1/2
-
2
/2
-
3
/2
-1/2
-
2
/2
-
3
/2
3
/2
2
/2
1/2
3
/2
2
/2
1/2
A
π
/3
π
/4
π
/6
3
/3
3
B
π
/2
3
/3
1
3
O
5. Ph ng trình đ cươ ộ
l p v i th i gian:ậ ớ ờ
ω
= +
2
2 2
2
v
A x
;
ω ω
= +
2 2
2
4 2
a v
A
Chú ý:
2
: Vaät qua vò trí caân baèng
: Vaät ôû bieân
MM
M
M
v A a
v
a A
ωω
ω
=
⇒ =
=
6. L c đàn h i, l c h i ph c: a. L c đàn h i: ự ồ ự ồ ụ ự ồ
( )
( ) ( ) neáu
0 neáu l A
ñhM
ñh ñhm
ñhm
F k l A
F k l x F k l A l A
F
= ∆ +
= ∆ + ⇒ = ∆ − ∆ >
= ∆ ≤
b. L c h i ph c: ự ồ ụ
0
hpM
hp
hpm
F kA
F kx F
=
= ⇒ =
hay
2
0
hpM
hp
hpm
F m A
F ma F
ω
=
= ⇒ =
l c h i ph c luôn h ng vào v trí cân b ng.ự ồ ụ ướ ị ằ
Go
ùc
Hslg
0
0300450 60090
0120013501500180
0360
0
0
6
π
4
π
3
π
2
π
3
2
π
4
3
π
6
5
π
π
π
2
sin
α
0
2
1
2
2
2
3
1
2
3
2
2
2
1
0 0
cos
α
1
2
3
2
2
2
1
0
2
1
−
2
2
−
2
3
−
-1 1
tg
α
0
3
3
1
3
kx
ñ
3−
-1
3
3
−
0 0
cotg
α
kx
ñ
3
1
3
3
0
3
3
−
-1
3−
kxñ kxñ
2

Chú ý: Khi h dao đ ng theo ph ng n m ngang thì l c đàn h i và l c h i ph c là nh nhau ệ ộ ươ ằ ự ồ ự ồ ụ ư
ñh hp
F F
=
.
7. Th i gian, quãng đ ng, t c đ trung bìnhờ ườ ố ộ
a. Th i gian:ờ Gi i ph ng trình ả ươ
cos( )
i i
x A t
ω ϕ
= +
tìm
i
t
Chú ý: - Th i gian :ờ
2
T
tAA =
→−
,
4
T
tAo =
±→
,
12
2
T
tA
o=
±→
,
8
2
2
T
tA
o
=
±→
,
6
2
3
T
tA
o
=
±→
- V n t c c c đ i khi qua v trí cân b ng (li đ b ng không), b ng không khi biên (li đ c c đ i).ậ ố ự ạ ị ằ ộ ằ ằ ở ộ ự ạ
b. Quãng đ ngườ :
Neáu thì
4
Neáu thì 2
2
Neáu thì 4
T
t s A
T
t s A
t T s A
= =
= =
= =
suy ra
Neáu thì 4
Neáu thì 4
4
Neáu thì 4 2
2
t nT s n A
T
t nT s n A A
T
t nT s n A A
= =
= + = +
= + = +
Chú ý: Quãng đ ng l n nh t : ườ ớ ấ
ax
2Asin 2
M
S
ϕ
∆
=
Quãng đ ng nh nh t : ườ ỏ ấ
2 (1 os )
2
Min
S A c
ϕ
∆
= −
Trong đó:
t∆=∆
ωϕ
2 2
2 neáu vaät ñi töø
2 2
neáu vaät ñi töø
4
M
s A x A x A
T
ts A x O x A
= = = ±
= → = = ↔ = ±
m
( )
2 2
2 2 neáu vaät ñi töø
2 2
2 2
neáu vaät ñi töø 0
2 2
82 2
1 neáu vaät ñi töø
2 2
m
M
m
s A x A x A x A
s A x x A
T
t
s A x A x A
= − = ± = ± = ±
= = ↔ = ±
= →
= − = ± ↔ = ±
÷
÷
( )
3 3
neáu vaät ñi töø 0
2 2
neáu vaät ñi töø
62 2
3 3
2 3 neáu vaät ñi töø
2 2
M
m
s A x x A
TA A
ts x x A
s A x A x A x A
= = ↔ = ±
= → = = ± ↔ = ±
= − = ± = ± = ±
neáu vaät ñi töø 0
2 2
3 3
12 1 neáu vaät ñi töø
2 2
M
m
A A
s x x
T
t
s A x A x A
= = ↔ = ±
= →
= − = ± ↔ = ±
÷
÷
c. T c đ trung bình và v n t c trung bình :ố ộ ậ ố
tb
s
vt
=
,
t
x
v∆
=
8. Năng l ng trong dao đ ng đi u hòa: ượ ộ ề
ñ t
E E E= +
a. Đ ng năng: ộ
2 2 2 2 2
1 1 sin ( ) sin ( )
2 2
ñ
E mv m A t E t
ω ω ϕ ω ϕ
= = + = +
b. Th năng: ế
2 2 2 2 2
1 1 cos ( ) cos ( );
2 2
t
E kx kA t E t k m
ω ϕ ω ϕ ω
= = + = + =
Chú ý:
2 2 2
2 2 2
2
1 1
2 2
1 1 : Vaät qua vò trí caân baèng
2 2
1: Vaät ôû bieân
2
ñM M
tM
E m A kA
E mv m A
E kA
ω
ω
= =
= =
=
3
12
T
3
2A
+
3
2A
−
2
2A
+
2
2A
−
1
2A
+
1
2A
−
A
+
A
−
x
6
T
6
T
6
T

Th năng và đ ng năng c a v t bi n thiên tu n hoàn v i ế ộ ủ ậ ế ấ ớ
ff 2
=
′
2
T
T
=
′
ωω
2
=
′
c a dao đ ng.ủ ộ
9. Chu kì c a h lò xo ghépủ ệ :
a. Ghép n i ti p: ố ế
2 2
1 2
1 2
1 1 1 T T T
k k k
= + ⇒ = +
b. Ghép song song:
1 2 2 2 2
1 2
1 1 1
T T T
k k k
= + ⇒ = +
c. Ghép kh i l ng: ố ượ
2 2
1 2 1 2
m m m T T T
= + ⇒ = +
Chú ý: Lò xo có đ c ng ộ ứ
0
k
c t làm hai ph n b ng nhau thì ắ ầ ằ
= = =
1 2 0
2k k k k
II. CON L C Đ NẮ Ơ
1. Ph ng trình li đ góc:ươ ộ
0
cos( )t
α α ω ϕ
= +
(rad)
2. Ph ng trình li đ dài:ươ ộ
0
cos( )s s t
ω ϕ
= +
3. Ph ng trình v n t c dài:ươ ậ ố
0
'; sin( )
ds
v s v s t
dt
ω ω ϕ
= = =− +
4. Ph ng trình gia t c ti p tuy n:ươ ố ế ế
22 2
0
2
'; ''; cos( );
t t t t
dv d s
a v a s a s t a s
dt dt
ω ω ϕ ω
= = = = =− + =−
Chú ý:
0
0
; s
s
l l
α α
= =
5. T n s góc, chu kì, t n s và pha dao đ ng, pha ban đ u:ầ ố ầ ố ộ ầ
a. T n s góc: ầ ố
2
2 ( / ); g mgd
f rad s
T l I
π
ω π ω
= = = =
b. T n s : ầ ố
1 1
( ); 2 2
N g
f Hz f
T t l
ω
π π
= = = =
c. Chu kì:
1 2
( ); 2
t l
T s T
f N g
ππ
ω
= = = =
d. Pha dao đ ng: ộ
( )t
ω ϕ
+
e. Pha ban đ u: ầ
ϕ
Chú ý: Tìm
ϕ
, ta d a vào h ph ng trình ự ệ ươ
0
0
cos
sin
s s
v s
ϕ
ω ϕ
=
= −
lúc
0
0t=
6. Ph ng trình đ c l p v i th i gian:ươ ộ ậ ớ ờ
ω
= +
2
2 2
02
v
s s
;
ω ω
= +
2 2
2
04 2
a v
s
Chú ý:
0
20
: Vaät qua vò trí caân baèng
: Vaät ôû bieân
MM
M
M
v s a
v
a s
ωω
ω
=
⇒ =
=
7. L c h i ph c:ự ồ ụ
L c h i ph c: ự ồ ụ
0
s
s
0
hpM
hp
hpm
g
F m
g
F m l
lF
=
= ⇒
=
l c h i ph c luôn h ng vào v trí cân b ng ự ồ ụ ướ ị ằ
8. Năng l ng trong dao đ ng đi u hòa:ượ ộ ề
ñ t
E E E= +
a. Đ ng năng: ộ
2 2 2 2 2
0
1 1 sin ( ) sin ( )
2 2
ñ
E mv m s t E t
ω ω ϕ ω ϕ
= = + = +
b. Th năng: ế
2 2 2 2 2
0
1 1
(1 cos ) cos ( ) cos ( );
2 2
t
g g g
E mgl m s m s t E t
l l l
α ω ϕ ω ϕ ω
= − = = + = + =
Chú ý:
2 2 2
0 0 0
2 2 2
0
2
0 0
1 1 (1 cos )
2 2
1 1 : Vaät qua vò trí caân baèng
2 2
1(1 cos ): Vaät ôû bieân
2
ñM M
tM
g
E m s m s mgl
l
E mv m s
g
E m s mgl
l
ω α
ω
α
= = = −
= =
= = −
4
α
0
α
F
P

Th năng và đ ng năng c a v t dao đ ng đi u hòa v i ế ộ ủ ậ ộ ề ớ
ff 2
=
′
2
T
T
=
′
ωω
2
=
′
V n t c: ậ ố
2
0 0
2 (1 cos ) 2 (cos cos )v v gl gl
α α α
=± − − =± −
L c căng dây: ự
0
(3cos 2cos )mg
τ α α
= −
9. S thay đ i chu kì dao đ ng c a con l c đ n:ự ổ ộ ủ ắ ơ
a. Theo đ cao (v trí đ a lí): ộ ị ị
2
0h
R
g g R h
= ÷
+
nên
2
h
h
l R h
T T
g R
π
+
= =
b. Theo chi u dài dây treo (nhi t đ ): ề ệ ộ
0
0
(1 )l l t
α
= + ∆
nên
α
π
∆
= = +
0
0
2 ( 1)
2
t
l t
T T
g
Th i gian con l c ch y nhanh (ch m trong 1s): ờ ắ ạ ậ
2 1
1 1
T TT
T T
−∆ =
Đ l ch trong m t ngày đêm: ộ ệ ộ
1
86400 T
T
θ
∆
=
c. N u ế
1 2
l l l= +
thì
2 2
1 2
T T T
= +
; n u ế
1 2
l l l= −
thì
2 2
1 2
T T T
= −
d. Theo l c l ự ạ
l
F
u
:
2 2
hay
hay 2
hay cos
l hd
l hd hd
hd
l hd
F P a g g g a
l
F P a g g g a T g
g
F P a g g g a
π
α
↑↑ ↑↑ ⇒ = +
↑↓ ↑↓ ⇒ = − ⇒ =
⊥ ⊥ ⇒ = + =
u u
u u
u u
Chú ý: L c l có th là l c đi n, l c t , l c đ y Acsimet, l c quán tính (ự ạ ể ự ệ ự ừ ự ẩ ự
qt
a a= −
uu
)
e. Đ bi n thiên:ộ ế
Chu kì tăng hay gi m theo %:ả
2 1
1
.100%
T T
T
−
Chi u dài tăng hay gi m theo %: ề ả
2 1
1
.100%
l l
l
−
Gia t c tăng hay gi m theo %: ố ả
2 1
1
.100%
g g
g
−
III. T NG H P DAO Đ NGỔ Ợ Ộ
1. Gi n đ Fresnel:ả ồ Hai dao đ ng đi u hòa cùng ph ng, cùng t n s và đ l ch pha không đ iộ ề ươ ầ ố ộ ệ ổ
1 1 1 2 2 2
cos( ) vaø cos( )x A t x A t
ω ϕ ω ϕ
= + = +
. Dao đ ng t ng h p ộ ổ ợ
1 2
cos( )x x x A t
ω ϕ
= + = +
có biên đ và pha đ c xácộ ượ
đ nh:ị
a. Biên độ:
2 2
1 2 1 2 1 2
2 cos( )A A A A A
ϕ ϕ
= + + −
; đi u ki nề ệ
1 2 1 2
A A A A A− ≤ ≤ +
b. Pha ban đ u ầ
ϕ
: tan
1 1 2 2
1 1 2 2
sin sin
cos cos
A A
A A
ϕ ϕ
ϕϕ ϕ
+
=+
; đi u ki n ề ệ
1 2 2 1
hoaëc
ϕ ϕ ϕ ϕ ϕ ϕ
≤ ≤ ≤ ≤
Chú ý:
ϕ π
ϕ π
π
ϕ
ϕ
∆ = = +
∆ = + = −
∆ = + = +
∆ = − ≤ ≤ +
1 2
1 2
2 2
1 2
1 2 1 2
Hai dao ñoäng cuøng pha 2 :
Hai dao ñoäng ngöôïc pha (2 1) :
Hai dao ñoäng vuoâng pha (2 1) :
2
Hai dao ñoäng coù ñoä leäch pha :
k A A A
k A A A
k A A A
const A A A A A
IV. DAO Đ NG T T D N, DAO Đ NG C NG B C, C NG H NGỘ Ắ Ầ Ộ ƯỠ Ứ Ộ ƯỞ
1. Dao đ ng t t d n:ộ ắ ầ
a. Ph ng trình đ ng l c h c: ươ ộ ự ọ
c
kx F ma− ± =
5
x
'x
O
A
u
1
A
uu
2
A
uu
ϕ






![Tài liệu ôn thi THPT Quốc gia Vật lý lớp 12 [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240403/vananh9a2kcr/135x160/5571712163061.jpg)



















