13
CHƯƠNG 8: HỢP CHUYỂN ĐỘNG CỦA ĐIỂM.
I. KHÁI NIỆM VỀ HỢP CHUYỂN ĐỘNG ĐIỂM.
1. Bài toán về hợp chuyển động điểm.
Trong thực tế chúng ta thường gặp trường hợp chất điểm trong một hệ quy chiếu nào
đó mà hệ quy chiếu ấy lại chuyển động so với hệ quy chiếu khác. Ví dụ một số trường hợp
sau:
- Một người chuyển động trên toa tầu và toa tầu chuyển động so với đường ray.
- Con thuyền chuyển động so với dòng nước và dòng nước chuyển động so với bờ
sông.
- Vệ tinh chuyển động xung quanh trái đất và trái đất chuyển động xung quanh mặt
trời. Trong các trường hợp trên ta phải dùng chính toa tầu, con thuyền, trái đất … làm hệ
quy chiếu động và khảo sát chuyển động của điểm trong hệ quy chiếu này đồng thời xét
chuyển động của hệ quy chiếu động so với hệ quy chiếu cố định là đường ray, bờ sông, mặt
trời.
2. Các định nghĩa về chuyển
động tuyệt đối, tương đối, theo.
Mô hình bài toán được thiết lập như sau:
Khảo sát chuyển động của điểm M trong hệ quy
chiếu động
Oxyz
. Hệ quy chiếu động
Oxyz
chuyển động trong hệ quy chiếu cố định
1111
Oxyz
. Ta có các định nghĩa sau:
a, Chuyển động tuyệt đối: là chuyển động
của M so với hệ quy chiếu cố định
1111
Oxyz
. Vận
tốc, gia tốc của M trong chuyển động tuyệt đối
được gọi là vận tốc tuyệt đối, gia tốc tuyệt đối và
được ký hiệu là
a
V
ur
,
a
W
uur
.
b, Chuyển động tương đối: là chuyển động của M so với hệ quy chiếu động
Oxyz
.
Vận tốc, gia tốc của M trong chuyển động tương đối được gọi là vận tốc tương đối, gia tốc
tương đối và được ký hiệu là
V
ur
,
r
W
uur
.
c, Chuyển động theo: là chuyển động của hệ quy chiếu động
Oxyz
so với hệ quy
chiếu cố định
1111
Oxyz
.
Để thiết lập biểu thức của vận tốc theo và gia tốc theo người ta đưa vào khái niệm
trùng điểm: trùng điểm của điểm M là điểm
*
M
cố định trong hệ động
Oxyz
mà tại lúc
khảo sát điểm M trùng với
*
M
. Vận tốc, gia tốc của
*
M
so với hệ quy chiếu cố định
1111
Oxyz
được gọi là vận tốc theo, gia tốc theo và được ký hiệu là
e
V
ur
,
e
W
uur
.
II. ĐỊNH LÝ HỢP VẬN TỐC.
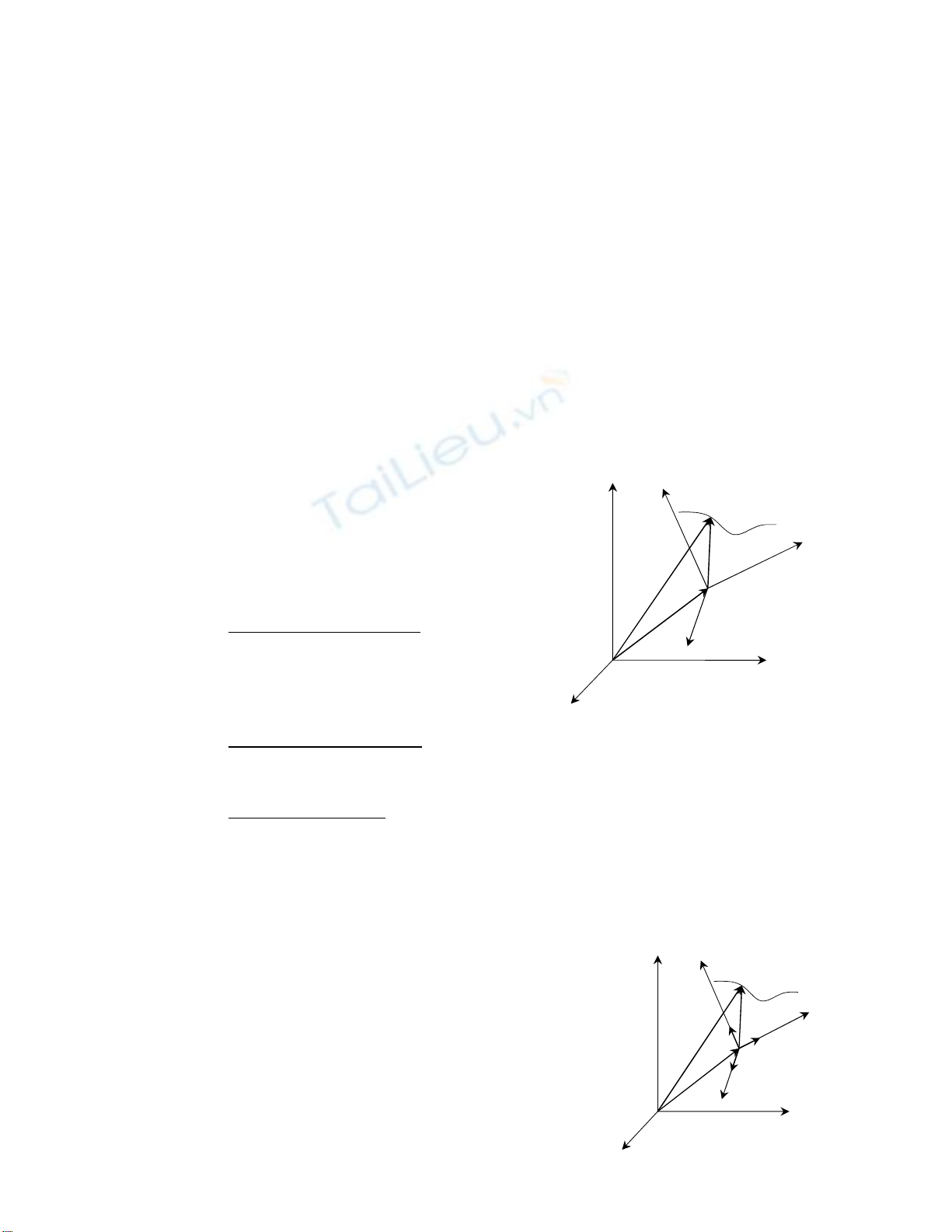
1. Định lý hợp vận tốc. Tại mỗi thời điểm, vận tốc
tuyệt đối của điểm bằng tổng hình học của vận tốc tương
đối và vận tốc theo.
aer
VVV
=+
ururur
(8.1)
2. Chứng minh.
M
O
y
x
z
1
z
1
y
x
1
O
r
r
*
MM
≡
O
z
y
x
x
1
y
1
z
r
r
i
r
j
r
k
r
1
O
14
Gọi
i,j,k
rrr
là các vectơ đơn vị thuộc hệ động
Oxyz
, toạ độ M trong hệ động là x,y,z.
Ta có:
OMx.iy.jz.k
=++
uuuur
rrr
Theo định nghĩa ta có:
-
(
)
r
dOM
V
dt
=
uuuur
ur ( đạo hàm theo thời gian vectơ
OM
uuuur
trong hệ động, tức
i,j,k
rrr
=const)
⇒ r
dxdydz
Vijk
dtdtdt
=++
ur
rrr
.
-
(
)
*
1
e
dOM
V
dt
=
uuuuur
ur ( đạo hàm theo thời gian vectơ
*
1
OM
uuuuur
trong hệ cố định, vì M* cố
định trong hệ động nên x,y,z=const)
⇒
(
)
()
()
*
1*
e11
dOM
dddidjdk
VOOOMOOxyz
dtdtdtdtdtdt
==+=+++
uuuuur
rrr
uuuuur
uruuuuruuuur
-
(
)
1
a
dOM
V
dt
=
uuuur
ur ( đạo hàm theo thời gian vectơ 1
OM
uuuur
trong hệ cố định)
⇒
(
)
()()
1
a11
dOM dd
VOOOMOO
dtdtdt
==+=
uuuur
uruuuuruuuuruuuur
+
dxdidydjdzdk
ixjykz
dtdtdtdtdtdt
+++++
rrr
rrr
⇔
()
a1
ddidjdkdxdydz
VOOxyzijk
dtdtdtdtdtdtdt
=++++++
rrr
uruuuur
rrr
=
er
VV
+
urur
(ĐPCM)
III. ĐỊNH LÝ HỢP GIA TỐC.
1. Định lý hợp gia tốc.
a, Định lý: Tại mỗi thời điểm, gia tốc tuyệt đối của điểm bằng tổng hình học của ba
thành phần gia tốc là gia tốc tương đối, gia tốc theo và gia tốc Côriôlít:
arec
WWWW
=++
uuruuruuruur
(8.2)
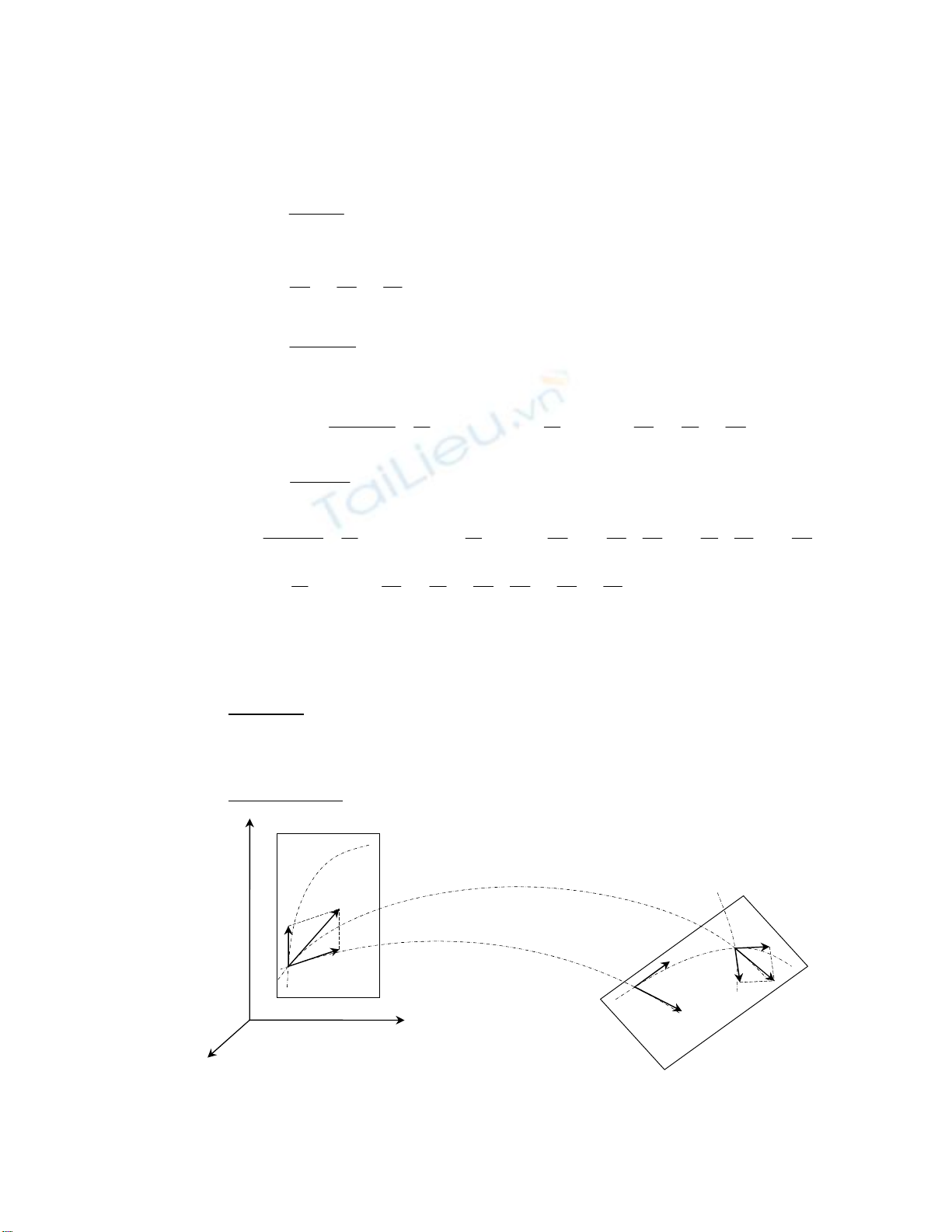
b,Chứng minh:
Giả sử :
- Tại thời điểm t hệ động tại vị trí (I) và tại thời điểm
ttt
′
=+∆
hệ động tại vị trí
(I’) như hình vẽ.
(I)
(I’
)
1
O
1
Z
1
Y
1
X
r
C
a
C
e
C
V
ur
a
V
ur
e
V
ur
*
MM
≡
e
C
′
r
C
′
*
1
M
r1
V
ur
e1
V
ur
M
′
r
V
′
uur
e
V
′
uur
a
V
′
uur
15
-
a
C
là quỹ đạo của M trong hệ cố định (tuyệt đối),
C
và
C
′
là quỹ đạo M trong hệ
động (tương đối),
e
C
là quỹ đạo
*
M
trong hệ cố định (theo),
e
C
′
là quỹ đạo của trùng
điểm với
M
′
.
-
r1
V
ur
là vị trí của
V
ur
tại thời điểm t mà ta tưởng tượng nó bị gắn chặt với hệ động
và bị hệ động kéo đi trong khoảng
t
∆
.
-
e1
V
ur
là vận tốc theo của
*
M
tại thời điểm
ttt
′
=+∆
.
Chú ý rằng
r
C
′
chỉ là sự dời chỗ của
r
C
sang vị trí mới mà thôi còn
e
C
′
và
e
C
thì là quỹ
đạo của hai điểm khác nhau cố định trên hệ động.
Theo định nghĩa gia tốc ta có:
- Gia tốc tương đối: Người quan sát đứng trên hệ động để khảo sát nên gia tốc
tương đối được xác định:
rr1
rt0
VV
Wlim
t
∆→
′−
=∆
uurur
uur
(a)
- Gia tốc theo: là gia tốc của trùng điểm
*
M
trong hệ cố định:
e1e
ct0
VV
Wlim
t
∆→
−
=∆
urur
uur
(b)
- Gia tốc tuyệt đối: là gia tốc của
M
trong hệ cố định:
aa
at0
VV
Wlim
t
∆→
′−
=∆
uurur
uur
(c)
Theo định lý hợp vận tốc thì
aer
VVV
′′′
=+
uuruuruur
và
aer
VVV
=+
ururur
nên ta có:
aaerereerr
VV(VV)(VV)(VV)(VV)
′′′′′
−=+−+=−+−
uururuuruurururuururuurur
(d)
Để đưa về dạng của (a), (b) ta biến đổi:
eeee1e1e
(VV)(VV)(VV)
′′
−=−+−
uururuurururur
và
rrrr1r1r
(VV)(VV)(VV)
′′
−=−+−
uururuurururur
(e)
Thay vào (d) ta có thể viết lại là:
aae1err1ee1r1r
VV(VV)(VV)(VV)(VV)

′′′
−=−+−+−+−

uururururuururuurururur
Thay vào (c) ta được:
e1err1ee1r1r
aa
a
t0t0
(VV)(VV)(VV)(VV)
VV
Wlimlim
tt
∆→∆→

′′
−+−+−+−
′
−

==
∆∆
ururuururuurururur
uurur
uur
⇔ e1err1ee1r1r
aerc
t0t0t0
VVVV(VV)(VV)
WlimlimlimWWW
ttt
∆→∆→∆→
′′
−−−+−
=++=++
∆∆∆
ururuururuurururur
uuruuruuruur
Trong đó
ee1r1r
ct0
(VV)(VV)
Wlim
t
∆→
′−+−
=∆
uurururur
uur
. Định lý đã được chứng minh.
Trong công thức
c
W
uur
gồm có hai thành phần. Thành phần đầu phản ánh sự biến thiên
của vận tốc theo khi M chuyển động trên hệ động. Thành phần thứ hai biểu thị sự đổi
hướng của vận tốc tương đối do chuyển động của hệ động gây ra.
2. Quy tắc thực hành xác định gia tốc Côriôlit.
a, Trường hợp hệ động chuyển đông tịnh tiến: Khi hệ động chuyển động tịnh tiến thì
ta có
r1r
VV
=
urur
, mặt khác các điểm cố định trên hệ động đều có vận tốc như nhau nên
ee1
VV
′=
uurur
. Do đó ta có c
W0
=
uur
.
b, Trường hợp hệ động chuyển đông quay quanh trục cố định: Giả sử hệ động quanh
trục cố định với vận tốc góc là
e
ω
r
. Người ta đã chứng minh được:
cr
e
W2.V
=ω∧
uurur
r
. (8.3)
Từ đó ta có một số quy tắc sau:
16
-
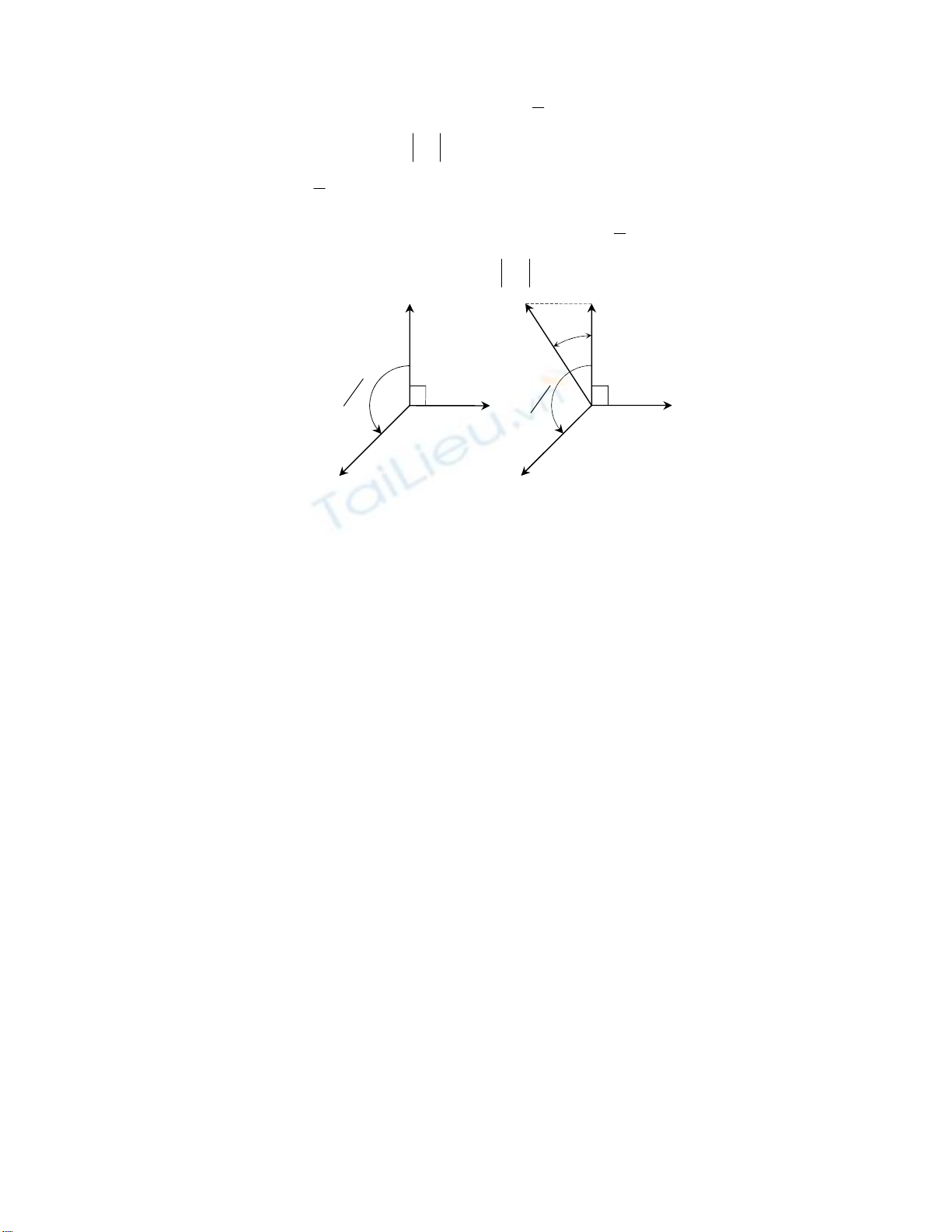
r
e
V
ω⊥
ur
r
: Quay
V
ur
quanh
e
ω
r
một góc
2
π
theo chiều quay của
e
ω
r
ta được hướng
của
c
W
uur
. Độ lớn được xác định c
er
W2..V
=ω
uur
.
-
·
r
e,V
2
π
ω≠
ur
r
: Chiếu
ur
V
lên phương vuông góc với
e
ω
r
trong mặt phẳng
chứa
V
ur
và
e
ω
r
ta được
r1
V
ur
. Quay
r1
V
ur
quanh
e
ω
r
một góc
2
π
theo chiều quay của
e
ω
r
ta
được hướng của
c
W
uur
. Độ lớn được xác định c
erer1
W2..V.cos2..V
=ωα=ω
uur
.
α
V
ur
2
π
e
ω
r
c
W
uur
2
π
r1
V
ur
V
ur
c
W
uur
e
ω
r