
12
CHƯƠNG 13: CÁC ĐỊNH LÝ TỔNG QUÁT ĐỘNG LỰC HỌC
I. ĐỊNH LÝ CHUYỂN ĐỘNG KHỐI TÂM CƠ HỆ.
1. Định lý chuyển động khối tâm cơ hệ.
Khối tâm của cơ hệ chuyển động như một chất điểm có khối lượng bằng khối lượng
của cơ hệ và chịu tác dụng của lực có vectơ lực bằng vectơ chính của hệ ngoại lực tác
dụng lên cơ hệ:
e
K
C
MWF
=
∑
uur r
(13.1)
Chứng minh:
Xét hệ có n chất điểm, hệ phương trình vi phân của nó là:
ei
11
1
1
ei
22
2
2
ei
nn
n
n
m.WFF
m.WFF
..........................
m.WFF
=+
=+
=+
uurr r
uurr r
uurr r
.
Cộng từng vế các phương trình của hệ ta được:
ei
KK
K
K
m.WFF
=+
∑∑∑
uurr r
.
Ta thấy i
K
F0
=
∑
r
nên
e
K
K
K
m.WF
=
∑∑
uur r
(*)
Mặc khác từ (12.1) ta có
CKK
r.Mm.r
=
∑
rr
Lấy đạo hàm hai lần đẳng thức này ta được:
CK
CKKK
r.Mm.rW.Mm.W
=⇔=
∑∑
uuruur
rr
&&&&
,
thay vào (*) ta được
e
K
C
MWF
=
∑
uur r
. Định lý đã được chứng minh.
Chiếu (13.1) lên các trục tọa độ ta được:
e
CKx
e
CKy
e
CKz
MxF
MyF
MzF
=
=
=
∑
∑
∑
&&
&&
&&
(13.2). Đây là phương
trình vi phân chuyển động khối tâm dưới dạng hình chiếu.
2. Định luật bảo toàn khối tâm cơ hệ.
Nếu vectơ chính của các ngoại lực tác dụng lên cơ hệ bằng không thì khối tâm của
cơ hệ đứng yên hoặc chuyển động thẳng đều.
Chứng minh: Từ (13.1) ta thấy nếu e
K
F0
=
∑
r
thì C
W0
=
uur
⇒C
Vc
osnt
=
ur
. Vậy nếu
ban đầu C
V0
=
ur
thì khối tâm cơ hệ đứng yên, còn nếu C
0
VV
=
ur
thì khối tâm cơ hệ chuyển
động thẳng đều với vectơ V0.
Hoàn toàn tương tự với (13.2) ta có định luật sau:
Nếu hình chiếu của vectơ chính của các ngoại lực lên một trục nào đó luôn luôn
bằng không thì hình chiếu của khối tâm cơ hệ trên trục đó đứng yên hoặc chuyển động
thẳng đều.
Định luật này gọi là “Định luật bảo toàn chuyển động của hình chiếu khối tâm cơ hệ”
II. ĐỊNH LÝ BIẾN THIÊN ĐỘNG LƯỢNG.
1. Động lượng của chất điểm và cơ hệ.
a, Động lượng chất điểm: Động lượng chất điểm là một đại lượng vectơ, ký hiệu là
q
r
bằng tích khối lượng của chất điểm với vận tốc của nó.
qm.V
=
ur
r
(13.3)

13
b, Động lượng cơ hệ: Động lượng cơ hệ (ký hiệu là
Q
ur
) là tổng hình học động lượng
các chất điểm thuộc cơ hệ.
K
K
Qm.V
=
∑
urur
(13.4)
Từ (12.1) ta được
KKC
m.rM.r
=
∑
rr
. Đạo hàm hai vế đẳng thức này theo t ta được:
KC
K
m.VM.V
=
∑
urur
. Hay là
C
QM.V
=
urur
. Như vậy động lượng của cơ hệ có thể xác định
bằng công thức
C
QM.V
=
urur
. Với M là khối lượng của cả cơ hệ,
C
V
ur
là vận tốc khối tâm cơ
hệ.
2. Xung lượng của lực(Xung lực).
Xung lượng nguyên tố của lực
F
r
là đại lượng vectơ, ký hiệu là
dS
r
, bằng tích của
lực
F
r
và dt.
dSF.dt
=
rr
(13.5)
Xung lượng của
F
r
trong khoảng thời gian hữu hạn từ
01
tt
→
là tích phân của xung
lực nguyên tố:
11
00
tt
tt
SdSF.dt
==
∫∫
rrr
. Nếu Fc
osnt
=
r
thì
(
)
10
SF.tt
=−
rr
.
Đơn vị của xung lực là Ns.
3. Các định lý biến thiên động lượng của chất điểm và cơ
hệ.
a, Định lý 1: Đạo hàm theo thời gian động lượng của chất điểm bằng hợp lực của
các lực tác dụng lên chất điểm đó.
()
(
)
K
dm.V
dq
F
dtdt
==
∑
ur
r
r
(13.6)
Chứng minh: Xét chất điểm M có khối lượng m, các lực tác dụng vào chất điểm là
12n
F,F,...,F
rrr
. Viết phương trình cơ bản động lực học cho M ta có:
(
)
K
dm.V
dVdq
FmWm
dtdtdt
====
∑
ur
ur
r
ruur (ĐPCM)
b, Định lý 2: Đạo hàm theo thời gian động lượng của cơ hệ bằng vectơ chính của
các ngoại lực tác dụng lên cơ hệ.
(
)
e
K
dQ
F
dt
=
∑
ur
r
(13.7)
Chứng minh: Xét chất điểm
K
M
có khối lượng
K
m
, các lực tác dụng vào chất điểm
gồm có ngoại lực
e
K
F
r
và nội lực
i
K
F
r
. Theo định lý 1 ta có:
(
)
K
ei
K
K
KK
dm.V
dq
FF
dtdt
==+
ur
r
rr
.
Cộng từng vế đẳng thức này ta được:
(
)
K
ei
K
KK
K
K
dm.V ddQ
m.VFF
dtdtdt
===+
∑∑∑∑
ur
ur
urr r
Chú ý là i
K
F0
=
∑
r
nên
e
K
dQ
F
dt
=
∑
ur
r
(ĐPCM)
c, Định lý 3: Biến thiên động lượng của chất điểm trong một khoảng thời gian nào
đó bằng tổng hình học xung lượng của các lực tác dụng lên chất điểm trong thời gian ấy.

14
1
0
t
K
10K
t
m.Vm.VF.dtS
−==
∑∑
∫
ururr r
(13.8)
Chứng minh: Từ (13.6) ta có
(
)
K
dm.VF.dt
=
∑
ur r
. Tích phân hai vế đẳng thức này
với cận tương ứng ta được
()
111
0
00
tt
V
KK
tt
V
dm.VF.dtF.dt
==
∑∑
∫∫∫
uur
uur
urr r
.
Hay là :
1
0
t
K
10K
t
m.Vm.VF.dtS
−==
∑∑
∫
ururr r
(ĐPCM)
d, Định lý 4: Biến thiên động lượng của cơ hệ trong một khoảng thời gian nào đó
bằng tổng hình học xung lượng của các ngoại lực tác dụng lên cơ hệ trong khoảng thời
gian ấy.
1
0
t
ee
K
K
10
t
QQF.dtS
−==
∑∑
∫
ururr r
(13.9)
Chứng minh: Từ (13.7) ta có
(
)
e
K
dQF.dt
=∑
ur r
. Tích phân hai vế đẳng thức này với
cận tương ứng ta được
()
111
0
00
tt
Vee
KK
tt
V
dQF.dtF.dt
==
∑∑
∫∫∫
uur
uur
urr r
.
Hay là :
1
0
t
ee
K
K
10
t
QQF.dtS
−==
∑∑
∫
ururr r
(ĐPCM)
Chú ý: Khi chiếu các đẳng thức trên lên các trục tọa độ đề các ta có các hệ sau:
- Chất điểm:
(
)
()
()
x
Kx
y
Ky
z
Kz
dm.V
F
dt
dm.V
F
dt
dm.V
F
dt
=
=
=
∑
∑
∑
ur
r
ur
r
ur
r
(13.10)
và
1
0
1
0
1
0
t
Kx
1x0xKx
t
t
Ky
1y0yKy
t
t
Kz
1z0zKz
t
m.Vm.VF.dtS
m.Vm.VF.dtS
m.Vm.VF.dtS
−==
−==
−==
∑∑
∫
∑∑
∫
∑∑
∫
ururr r
ururr r
ururr r
(13.11)

15
- Cơ hệ:
(
)
()
()
e
x
Kx
e
y
Ky
e
z
Kz
dQ
F
dt
dQ
F
dt
dQ
F
dt
=
=
=
∑
∑
∑
ur
r
ur
r
ur
r
(13.12) và
e
Kx
1x0x
e
Ky
1y0y
e
Kz
1z0z
QQS
QQS
QQS
−=
−=
−=
∑
∑
∑
urur r
urur r
urur r
(13.13)
Trong các công thức trên ta không thấy sự có mặt của nội lực. Vậy nội lực không làm
biến đổi động lượng của hệ.
Các định lý trên thường được sử dụng cho các bài toán va chạm và các bài toán về
chuyển động trong môi trường liên tục. Sau đây ta xét một số trường hợp mà động lượng
được bảo toàn.
4. Định luật bảo toàn động lượng.
Ta chỉ xét cho trường hợp cơ hệ, đối với chất điểm được xem như mọt trường hợp
riêng của cơ hệ.
a, Định lý 5: Nếu vectơ chính của các ngoại lực tác dụng lên cơ hệ luôn luôn bằng
không thì động lượng của cơ hệ được bảo toàn.
e
K
F0Qc
osnt
=⇔=
∑
rur
(13.14)
Chứng minh: Nếu e
K
F0
=
∑
r
, từ (13.7) ta có
(
)
e
K
dQ F0Qc
dt
osnt
==⇒=
∑
ur
rur .
(ĐPCM)
b, Định lý 6: Nếu hình chiếu của vectơ chính của các ngoại lực lên một trục nào đó
luôn luôn bằng không thì hình chiếu động lượng của cơ hệ lên trục ấy được bảo toàn.
Chứng minh: Nếu e
Kx
F0
=
∑
r
, ta có
(
)
e
x
Kx x
dQ F0Qc
dt
osnt
==⇒=
∑
ur
rur . (ĐPCM)
III. ĐỊNH LÝ BIẾN THIÊN MÔMEN ĐỘNG LƯỢNG.
1. Mômen động lượng của chất điểm và cơ hệ.
a, Mômen động lượng của chất điểm:
- Mômen động lượng của chất điểm đối với tâm O là một vectơ ký hiệu là l
O
là
mômen của vectơ động lượng đối với điểm O.
()
(
)
OOO
lmqmm.Vrm.V
===∧
urur
r
rrrr
(13.15)
- Mômen động lượng của chất điểm đối với trục z là một lượng đại số ký hiệu là lz
()
(
)
()
ZZZ
lmqmm.Vm.V.h
′
===±
ur
rrr
(13.16)
Trong đó
m.V
′
là hình chiếu của
m.V
ur
lên mặt phẳng π vuông góc với trục z, h là
khoảng cách từ O (là giao điểm của mặt phẳng π với trục z) đến
m.V
′
. Lấy dấu cộng khi
nhìn từ trục z xuống mặt phẳng π thấy
V
′
uur
quay quanh O theo ngược chiều kim đồng hồ.
Tương tự mômen lực ở tĩnh học ta cũng có: Mômen động lượng của chất điểm đối
với một trục bằng hình chiếu lên trục ấy của vectơ mômen động lượng của chất điểm đối
với một điểm thuộc trục.
(
)
(
)
zOzOz
hclhcmFmF
==
rr
r
r
(13.17)
16
Gọi x,y,z là tọa độ của chất điểm và
xyz
V,V,V
là hình chiếu vận tốc chât điểm ấy lên
các trục tọa độ. Từ (13.15) ta có: O
xyz
ijk
lrm.Vxyz
mVmVmV
=∧=
rrr
ur
rr. (13.18)
Tương tự công thức (1.2) ta cũng có:
(
)
()
()
xZy
yxz
zyx
lmy.Vz.V
lmz.Vx.V
lmx.Vy.V
=−
=−
=−
(13.19)
b, Mômen động lượng của cơ hệ:
- Mômen động lượng của cơ hệ đối với một tâm bằng tổng mômen động lượng của
các chất điểm thuộc cơ hệ với cùng tâm đó.
()
(
)
O
KK
OKOKKK
Lmqmm.Vrm.V
===∧
∑∑∑
ururur
rrrr
(13.20)
- Mômen động lượng của cơ hệ đối với một trục bằng tổng mômen động lượng của
các chất điểm thuộc cơ hệ với cùng trục đó.
()
(
)
K
ZZKZK
Lmqmm.V
==
∑∑
ur
rrr
(13.21)
Đơn vị của mômen động lượng là: kgm2/s
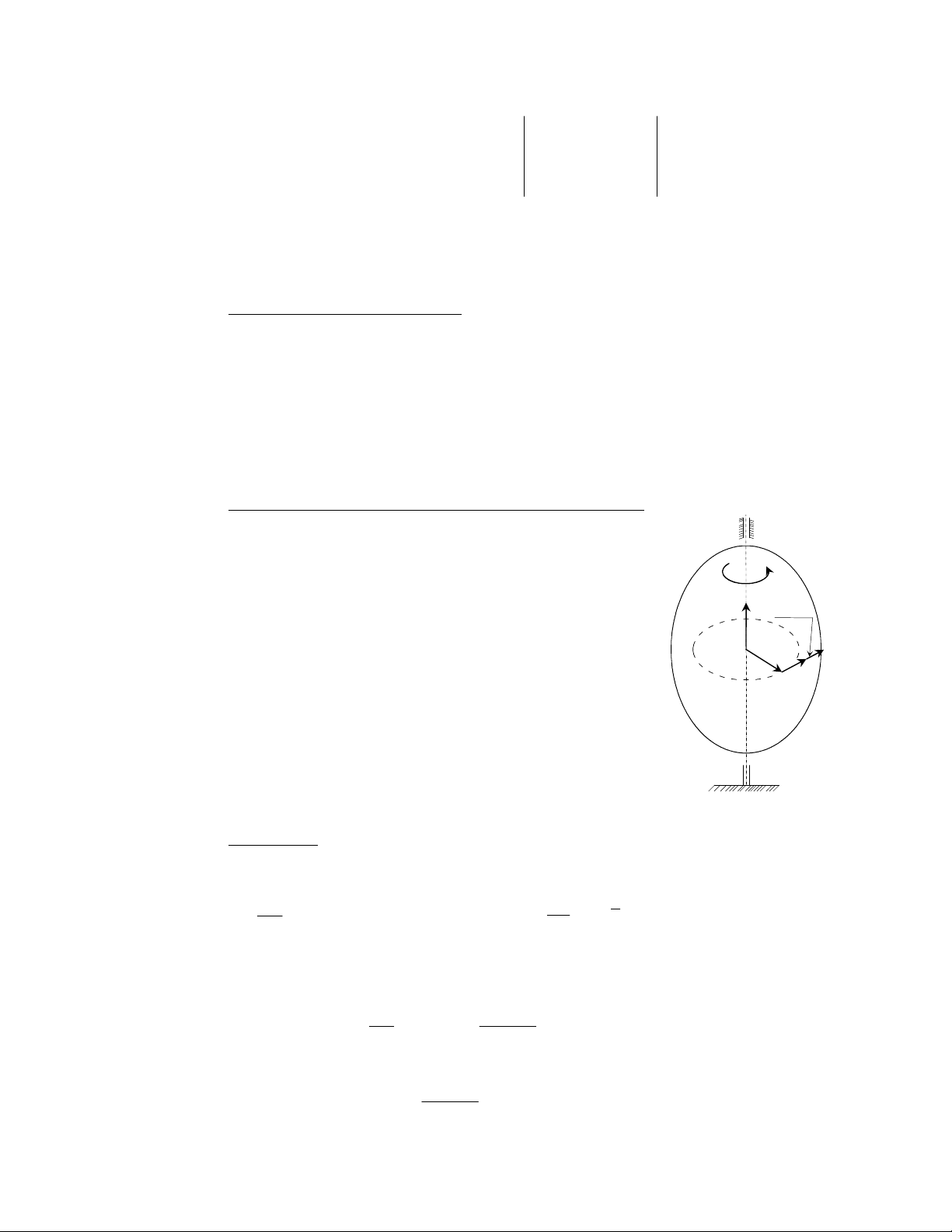
c, Mômen động lượng của vật rắn quay quanh trục cố định:
Xét vật rắn quay quanh trục cố định z với vận tốc góc là ω.
Mômen động lượng của chất điểm
K
M
với trục z là:
(
)
K
KZZK
lmm.V
=
ur
r
. Do
K
K
m.V
ur
nằm trên mặt phẳng chứa
K
M
và
K
r
r
nên
KZKKK
lr.m.V
=±
. Theo hình vẽ ta lấy dấu cộng vậy
KZKKK
lr.m.V
=
. Mặc khác
KK
V.r
=ω
nên ta có
2
KZKK
l.m.r
=ω .
Mômen động lượng của cả vật đối với trục z là:
(
)
2
ZZKKK
Lmq.m.r
==ω
∑∑
rr
Theo (12.3) thì
22
zKKKK
Jm.dm.r
==
∑∑
, vậy ta được:
Zz
L.J
=ω
(13.22)
2. Định lý biến thiên mômen động lượng của
chất điểm và cơ hệ.
a, Định lý 1: Đạo hàm theo thời gian mômen động lượng của chất điểm đối với một
tâm (với một trục) cố định bằng tổng mômen các lực tác dụng lên chất điểm đối với cùng
tâm (trục) đó.
()
O
K
O
dl
mF
dt
=∑
r
r
r (13.23) và
()
z
K
z
dl
mF
dt
=∑
r
(13.24)
Chứng minh: Xét chất điểm M, có khối lượng m, chịu tác dụng của hệ lực
(
)
12n
F,F,...,F
rrr
. Phương trình cơ bản của động lực học:
(
)
KKK
dm.V
dV
m.WFm.FF
dtdt
=⇔=⇔=
∑∑∑
ur
ur
uurrr r
Gọi
r
r
là vectơ định vị chất điểm, nhân hai vế đẳng thức trên với
r
r
ta được:
(
)
K
dm.V
rrF
dt
∧=∧
∑
ur
r
rr
(*)
ω
r
k
r
r
k
M
k
V
ur
k
m.V
ur











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














