1
MỞ ĐẦU
ĐỐI TƯỢNG VÀ PHƯƠNG PHÁP NGHIÊN CỨU CỦA MÔN HỌC.
Cơ học lý thuyết là môn học nghiên cứu những quy luật cân bằng và chuyển động
của các vật thể. Chuyển động được hiểu là sự thay đổi vị trí của các vật thể trong không
gian theo thời gian. Vật thể được biểu diễn dưới dạng những mô hình, đó là chất điểm và
cơ hệ.
Để mô tả chuyển động của vật thể người ta phải dùng hệ quy chiếu, tức là những vật
chuẩn hoặc những hệ tọa độ gắn với vật chuẩn ấy.
Ví dụ: con tàu chuyển động so với ngôi nhà, như vậy ngôi nhà là vật chuẩn và người
ta gắn với ngôi nhà một hệ quy chiếu để khảo sát chuyển động của con tàu.
Một hệ quy chiếu mà trong đó vật thể chuyển động với vận tốc không đổi khi không
có lực tác dụng thì được gọi là hệ quy chiếu quán tính. Nói cách khác, trong hệ quy chiếu
quán tính nếu không có lực tác dụng chất điểm sẽ chuyển động thẳng và đều. Chuyển động
này được gọi là chuyển động quán tính.
Chú ý: trong chuyển động tròn đều vận tốc không đổi về mặt giá trị nhưng phương
của vận tốc thay đổi nên không được coi là chuyển động quán tính.
Mọi hệ quy chiếu chuyển động thẳng và đều với hệ quy chiếu quán tính cũng là hệ
quy chiếu quán tính. Do vậy ta có vô số hệ quy chiếu quán tính chuyển động thẳng đều với
nhau.
Cơ học lý thuyết dựa trên những nguyên lý của Niutơn, được gọi là cơ học cổ điển.
Cơ học cổ điển nghiên cứu chuyển động với vận tốc nhỏ hơn vận tốc ánh sáng trong chân
không (3.108 m/s).
Cơ học lý thuyết được xây dựng theo phương pháp hiện đại của toán học là phương
pháp tiền đề, dựa trên những khái niêm cơ bản và một hệ tiên đề. Những khái niệm cơ bản
là những khái niệm đầu tiên, không định nghĩa. Các tiền đề là các mệnh đề phát biểu công
nhận tính chất của một số khái niệm cơ bản và cũng không chứng minh.
Cơ học lý thuyết ngoài việc cung cấp các kiến thức về cơ học nó còn là cơ sở của các
môn học khác như Sức bền vật liệu, Nguyên lý máy, Chi tiết máy ...
Môn học này gồm ba phần chính là Tĩnh học vật rắn, Động học và Động lực học.
1
A
B
D
E
a
PHẦN I: TĨNH HỌC VẬT RẮN
MỞ ĐẦU
Tĩnh học là phần khảo sát trạng thái cân bằng (tĩnh) của vật rắn dưới tác dụng của
các lực. Có hai vấn đề lớn được nghiên cứu trong phần này là:
Thu gọn hệ lực: là biến đổi hệ lực tác dụng lên vật thành một hệ lực khác tương
đương nhưng có dạng đơn giản hơn. Khi hệ lực được biến đổi về dạng đơn giản nhất thì hệ
lực đó được gọi là dạng tối giản của hệ lực ban đầu.
Tìm điều kiện cân bằng: là thiết lập các điều kiện đối với hệ lực mà dưới tác dụng
của nó vật rắn cân bằng, gọi tắt là các điều kiện cân bằng của hệ lực.
CHƯƠNG 1: CÁC KHÁI NIỆM CƠ BẢN – HỆ TIÊN ĐỀ TĨNH HỌC
§ I. CÁC KHÁI NIỆM CƠ BẢN CỦA TĨNH HỌC.
1. Vật rắn tuyệt đối.
Vật rắn tuyệt đối là tập hợp vô hạn các chất điểm mà khoảng cách giữa hai chất
điểm bất kỳ luôn luôn không đổi.
Trong thực tế các vật khi chịu lực đều bị biến dạng. Nếu biến dạng đó quá bé hoặc
biến dạng không làm ảnh hưởng đến kết quả của bài toán khảo sát thì có thể bỏ qua biến
dạng và như vậy có thể coi là vật rắn tuyệt đối. Vật rắn tuyệt đối được gọi tắt là vật rắn.
2. Vật rắn cân bằng.
Vật rắn được coi là cân bằng trong một hệ quy chiếu nào đó nếu nó đứng yên hay
chuyển động tịnh tiến thẳng và đều đối với hệ quy chiếu ấy.
Chuyển động tịnh tiến thẳng và đều là chuyển động mà mọi điểm thuộc vật rắn đều
chuyển động thẳng với vận tốc không đổi.
3. Lực.
Lực là đại lượng biểu thị tác dụng cơ học của vật thể này lên vật thể khác. Lực là
một đại lượng có hướng, qua thực nghiệm người ta đã xác định được lực có các yếu tố đặc
trưng sau:
Ø Điểm đặt của lực: là điểm mà vật nhận được tác dụng cơ học từ vật khác.
Ø Phương, chiều của lực: là phương, chiều chuyển động của chất điểm (vật có kích
thước bé) từ trạng thái cân bằng khi chịu tác dụng của lực ấy.
Ø Cường độ của lực: là đại lượng xác định độ mạnh hay yếu của lực, xác định bằng
cách so với một lực chuẩn gọi là lực đơn vị. Đơn vị của lực là Niutơn, ký hiệu là N.
Lực được biểu diễn bằng một vectơ như hình 1-1, gọi là vectơ lực. Vectơ lực có
những đặc trưng sau:
Ø Điểm đặt (A) của vectơ là điểm đặt của lực.
Ø Phương, chiều của vectơ lực (
AB
uuur
) trùng với phương, chiều
của lực.
Ø Độ dài a của vectơ
AB
uuur
biểu diễn cường độ của lực.
Vectơ lực thường được ký hiệu là
F,P
rur
hoặc
Q
ur
. Đường thẳng DE
chứa vectơ lực
AB
uuur
được gọi là đường tác dụng của lực.
4. Các định nghĩa khác về lực.
a, Hệ lực: là tập hợp nhiều lực cùng tác dụng lên một vật rắn hay một chất điểm. Hệ
lực gồm các lực
F,F,...,F
rrr
được ký hiệu là
(
)
12n
F,F,...,F
rrr
.
2
b, Hệ lực tương đương: Hai hệ lực có cùng tác dụng cơ học thì được gọi là hai hệ
lực tương đương.
Hệ lực
(
)
12n
F,F,...,F
rrr
và hệ lực
(
)
12n
P,P,...,P
ururur
tương đương nhau thì được ký hiệu là:
(
)
(
)
12n12n
F,F,...,FP,P,...,P
≡
rrrururur
.
c, Hệ lực cân bằng: Hệ lực cân bằng là hệ lực nếu tác dụng lên vật rắn sẽ không
làm thay đổi trạng thái cơ học mà vật đang có. Hệ lực cân bằng còn được gọi là hệ lực
tương đương với không và được ký hiệu:
(
)
12n
F,F,...,F0
=
rrr
.
d, Hợp lực của hệ lực: Nếu hệ lực đã cho tương đương với một lực duy nhất thì lực
ấy được gọi là hợp lực của hệ lực đã cho. Nếu
R
ur
là hợp lực của hệ lực
(
)
12n
F,F,...,F
rrr
thì
ta ký hiệu:
(
)
12n
RF,F,...,F
≡
urrrr
.
§ II. KHÁI NIỆM VỀ MÔMEN LỰC.
1. Mômen của lực đối với một điểm.
a, Định nghĩa: Mômen của lực
ur
F
đối với điểm O là một vectơ, ký hiệu là
(
)
ur
r
O
mF
, có
các tính chất sau:
Ø Điểm đặt: tại O
Ø Phương: vuông góc với mặt phẳng π chứa lực
F
r
và điểm O.
Ø Chiều: Xác định theo quy tắc cái đinh ốc (quay
cái đinh ốc theo chiều của lực
F
r
quanh O, chiều tiến
của cái đinh ốc là chiều vectơ mômen).
Ø Độ lớn: bằng tích số của cường độ lực
F
r
với
cánh tay đòn d (d =OH).
(
)
(
)
OO
mFFdFrsin(r,F)mFrF
==⇒=∧
rrrr
rrrr
... .
b, Tính chất:
(
)
O
mF
r
r
là đại lượng đặc trưng cho tác dụng quay của lực
F
r
quanh tâm
O. Ta thấy
(
)
O
mF0 Fd0
=⇔=
r
r
., có hai trường hợp xảy ra:
Ø
F0
=
: Trường hợp này không có lực tác dụng.
Ø
d0
=
: Trường hợp này đường tác dụng của lực qua tâm O.
Khi các lực
F,F,...,F
rrr
nằm trong cùng mặt phẳng (đồng phẳng) thì các vectơ
(
)
i
O
mF
r
r
(i=1→n) cùng phương. Do đó người ta đưa ra khái niệm mômen đại số của lực
F
r
đối với điểm O, ký hiệu là
(
)
O
mF
r
.
(
)
O
mFF.d
=±
r
, lấy dấu + khi
F
r
vòng quanh O ngược
chiều kim đồng hồ và ngược lại.
(
)
OOAB
mFFd2S∆
==
r
r
., (
OAB
S∆ là diện tích tam giác OAB)
c, Biểu thức: Gọi x,y,z là tọa độ điểm đặt lực A trong hệ tọa độ Oxyz,
xyz
F,F,F
là
hình chiếu của lực
F
r
lên các trục Ox, Oy, Oz.
i,j,k
rrr
.
Theo định nghĩa ta có:
()
O
xyz
ijk
mFrFxyz
FFF
=∧=
rrr
rr
rr (1-1)
π
F
r
B
A
O
H
d
(
)
O
mF
r
r
r
r
3
Hình chiếu của
(
)
O
mF
r
r
lên các trục là:
() ()
() ()
() ()
OzyOx
x
OxzOy
y
OyxOz
z
mFy.Fz.FmF
mFz.Fx.FmF
mFx.Fy.FmF

=−=


=−=


=−=

rr
r
rr
r
rr
r
(1-2)
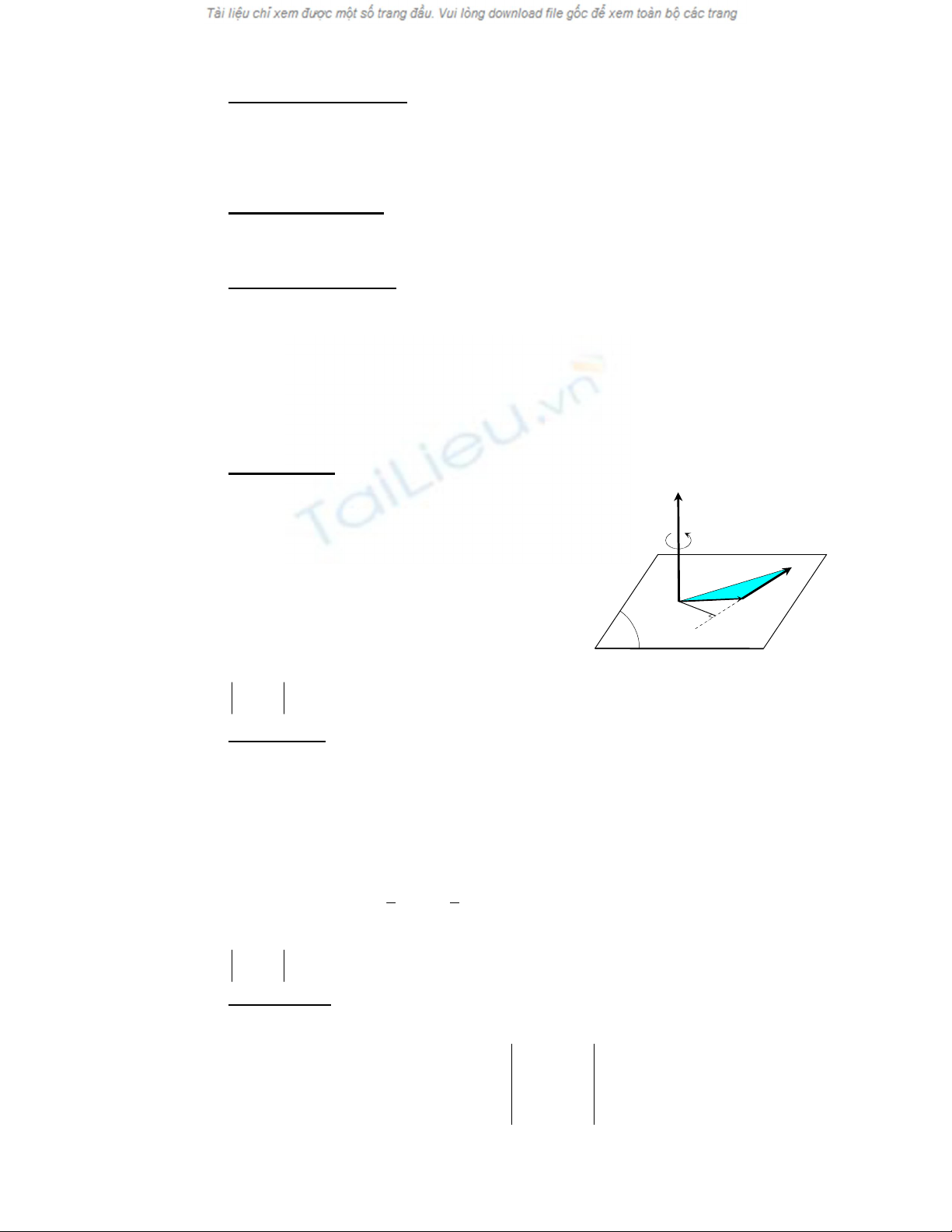
2. Mômen của lực đối với một trục.
a, Định nghĩa: Mômen của lực
ur
F
đối với trục ∆ ký hiệu là
(
)
∆
ur
mF
, là mômen đại số
của lực
′
uur
F
đối với điểm O, với
′
uur
F
là hình chiếu của lực
ur
F
lên mặt phẳng π vuông góc trục
∆ còn O là giao điểm giữa trục ∆ và mặt phẳng π.
(
)
(
)
O
mFmF
∆
′
=
rur
(1-3)
b, Tính chất:
(
)
(
)
O
mF0mFF.d0
∆′′
=⇔==
rur
Ø
F0
′
=
: Đường tác dụng của lực
F//
∆
r
.
Ø
d0
=
: Đường tác dụng của lực
F
r
cắt trục
∆
.
Trong cả hai trường hợp này ta thấy đường tác
dụng của lực
F
r
và
∆
đồng phẳng. Do đó khi xét hệ lực
đồng phẳng và trục cũng nằm trong mặt phẳng ấy thì không cần đưa
ra khái niệm này.
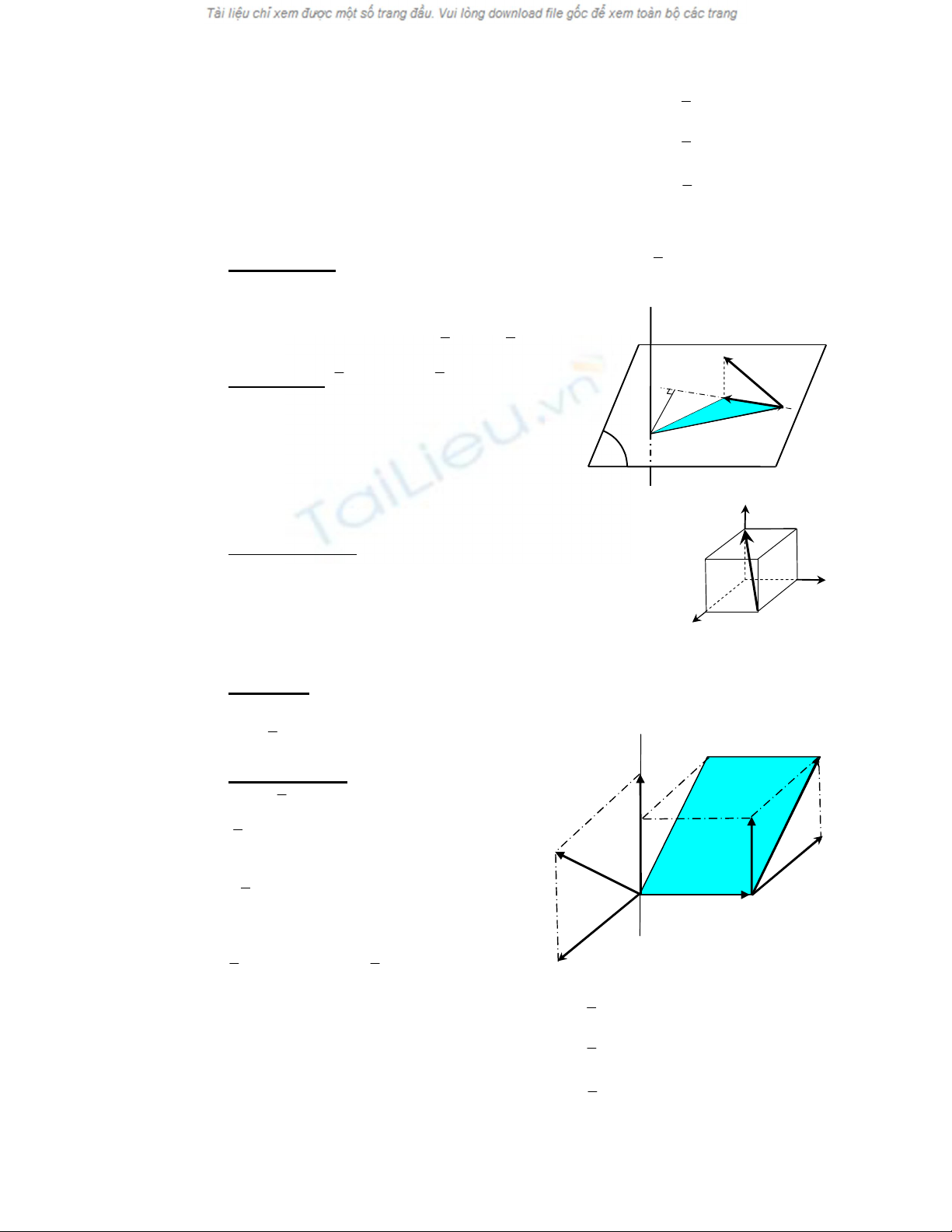
Vid due adp dueng: Cho lực
F
r
là đường chéo hình lập phương
cạnh a như hình vẽ hãy xác định:
(
)
O
mF
r
r
,
(
)
(
)
(
)
OOO
xyz
mF,mF,mF


rrr
rrr
.
3. Định lý liên hệ giữa mômen lực đối với
điểm và đối với trục.
a, Định lý: Mômen của lực
ur
F
đối với trục ∆ bằng hình chiếu lên trục ấy của vectơ
mômen của lực
ur
F
đối với tâm O ngay trên trục∆.
(
)
(
)
O
mFmF
∆
∆

=

rr
r
(1-3)
b, Chứng minh: Phân tích lực
12
FFF
=+
rrr
.
Ta có
(
)
(
)
12
O
mFrFrFF
=∧=∧+
rrrr
rr
hay
(
)
12
O
mFrFrF
=∧+∧
rrr
rr
Chiếu lên trục ∆ ta được:
(
)
12
O
mFrFrF
∆∆
∆


=∧+∧


rrr
rr
Rõ ràng 2
rF0
∆

∧=

r
r
và
11
rFrF
∆

∧=∧

rr
rr
vậy:
(
)
(
)
1
O
mFrFmF
∆
∆

=∧=

rrr
r
(ĐPCM)
Áp dụng định lý trên cho các trục tọa độ ta được:
()()
()()
()()
xO
x
yO
y
zO
z
mFmF
mFmF
mFmF

=


=


=

rr
r
rr
r
rr
r
h (1-4)
F
r
F
′
ur
A
B1
B
d
∆
π
F
r
r
r
1
F
r
2
F
r
rF
∧
r
r
2
rF
∧
r
r
1
rF
∧
r
r
∆
O
F
r
O
x
y
z
4
§ III. HỆ TIÊN ĐỀ TĨNH HỌC.
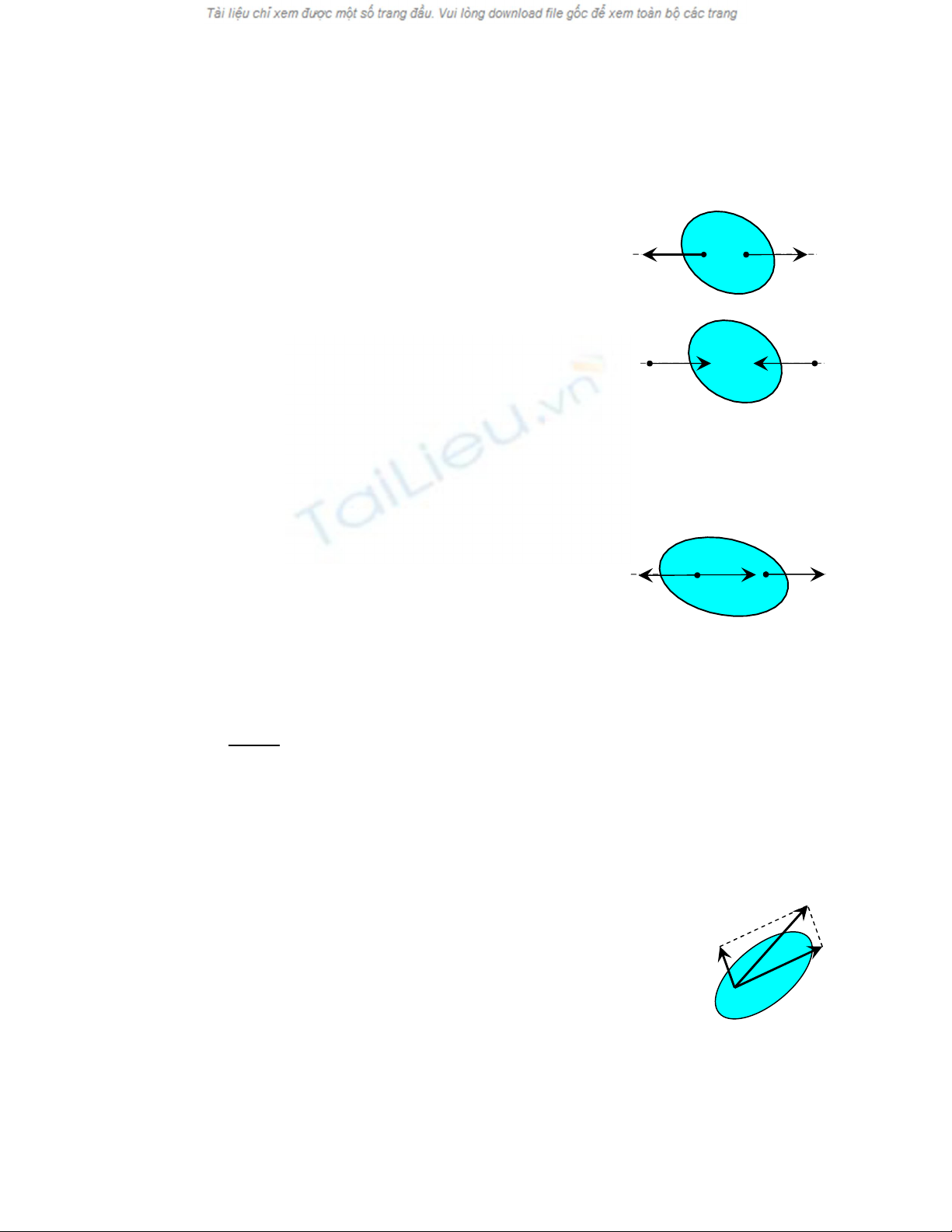
1. Tiên đề 1 (tiên đề về hai lực cân bằng).
Điều kiện cần và đủ để hai lực cân bằng là chúng có cùng đường tác dụng, hướng
ngược chiều nhau và có cùng cường độ.
Hai lực
F
r
và
F
′
ur
cân bằng được ký hiệu:
(
)
F,F0
′
=
rur
.
Hai lực như thế còn được gọi là hai lực trực đối. Hình a
cho ta hình ảnh về vật rắn cân bằng chịu kéo và hình 1-6 là
vật rắn cân bằng chịu nén.
Tiên đề 1 nêu lên một hệ lực cân bằng chuẩn giản đơn
nhất. Khi cần xác định hệ lực đã cho có cân bằng hay không
ta tìm cách biến đổi để chứng minh nó có tương đương với
hai lực cân bằng hay không.
2. Tiên đề 2 (tiên đề thêm bớt lực).
Tác dụng của hệ lực không thay đổi nếu ta thêm vào
hoặc bớt đi một cặp lực cân bằng.
Nếu
(
)
F,F0
′
=
rur
thì
(
)
(
)
12n12n
F,F,...,FF,F,...,F,F,F
′
≡
rrrrrrrur
.
Tiên đề này cho ta hai phép biến đổi cơ bản là thêm vào một cặp lực cân bằng và bớt
đi một cặp lực cân bằng.
* Hệ quả 2.1 (Định lý trượt lực): Tác dụng của lực không thay đổi khi ta trượt lực
trên đường tác dụng của nó.
Chứng minh: Cho lực
F
r
tác dụng lên vật rắn tại A.
Tại điểm B thuộc đường tác dụng của lực
F
r
ta thêm vào hai
lực cân bằng
(
)
12
F,F
rr
như hình vẽ.
Theo tiên đề 2:
(
)
(
)
1212
FF,F,FF,FF
==+
rrrrrrr
. Theo tiên đề 1 ta có
(
)
1
F,F
rr
là cặp lực cân
bằng vậy theo tiên đề 2 ta có thể bỏ đi. Do đó
2
FF
=
rr
.
Từ định lý trên ta thấy điểm đặt không giữ vai trò gì trong việc mô tả tác dụng của
lực lên vật rắn.
Chú ý: Tính chất trên chỉ đúng với vật rắn tuyệt đối. Với vật rắn biến dạng khi thay
đổi điểm đặt thì ứng xử của biến dạng trong vật sẽ thay đổi.
* Hệ quả 2.2 (Định lý về hợp lực của hệ): Khi hệ lực cân bằng thì một lực bất kỳ của
hệ lực ấy sẽ là lực trực đối với hợp lực của các lực còn lại.
Chứng minh: Cho hệ lực
(
)
12n
F,F,...,F0
=
rrr
, đặt
(
)
2n
RF,...,F
=
urrr
, ta có:
(
)
(
)
12n1
F,F,...,FF,R0
==
rrrrur
, có nghĩa là
1
F
r
là lực trực đối với
R
ur
hay
1
F
r
là lực trực
đối với hợp lực của các lực
(
)
2n
F,...,F
rr
.
3. Tiên đề 3 (tiên đề hình bình hành lực).
Hệ hai lực cùng đặt tại một điểm tương đương với một lực đặt tại
điểm đặt chung ấy và được biểu diễn bằng vectơ đường chéo hình bình
hành mà hai cạnh là hai vectơ biểu diễn các lực đã cho.
(
)
1212
F,FRFF
==+
rrurrr
Tiên đề này cho ta hai phép biến đổi cơ bản, đó là: có thể tổng hợp hai lực đồng quy
thành một lực và ngược lại có thể phân tích một lực thành hai lực đồng quy theo quy tắc
hình bình hành.
* Hệ quả 3.1 (Định lý về đường tác dụng của 3 lực đồng phẳng): Khi ba lực đồng
phẳng cân bằng, đường tác dụng của chúng hoặc đồng quy hoặc song song.
B
A
2
F
r
F
r
1
F
r
A
1
F
r
2
F
r
R
ur
A
B
F
′
ur
F
r
Hình a
A
B
F
′
ur
F
r
Hình b