Trần Sĩ Tùng Đại số 11
Trang 1
I. HỆ THỨC CƠ BẢN
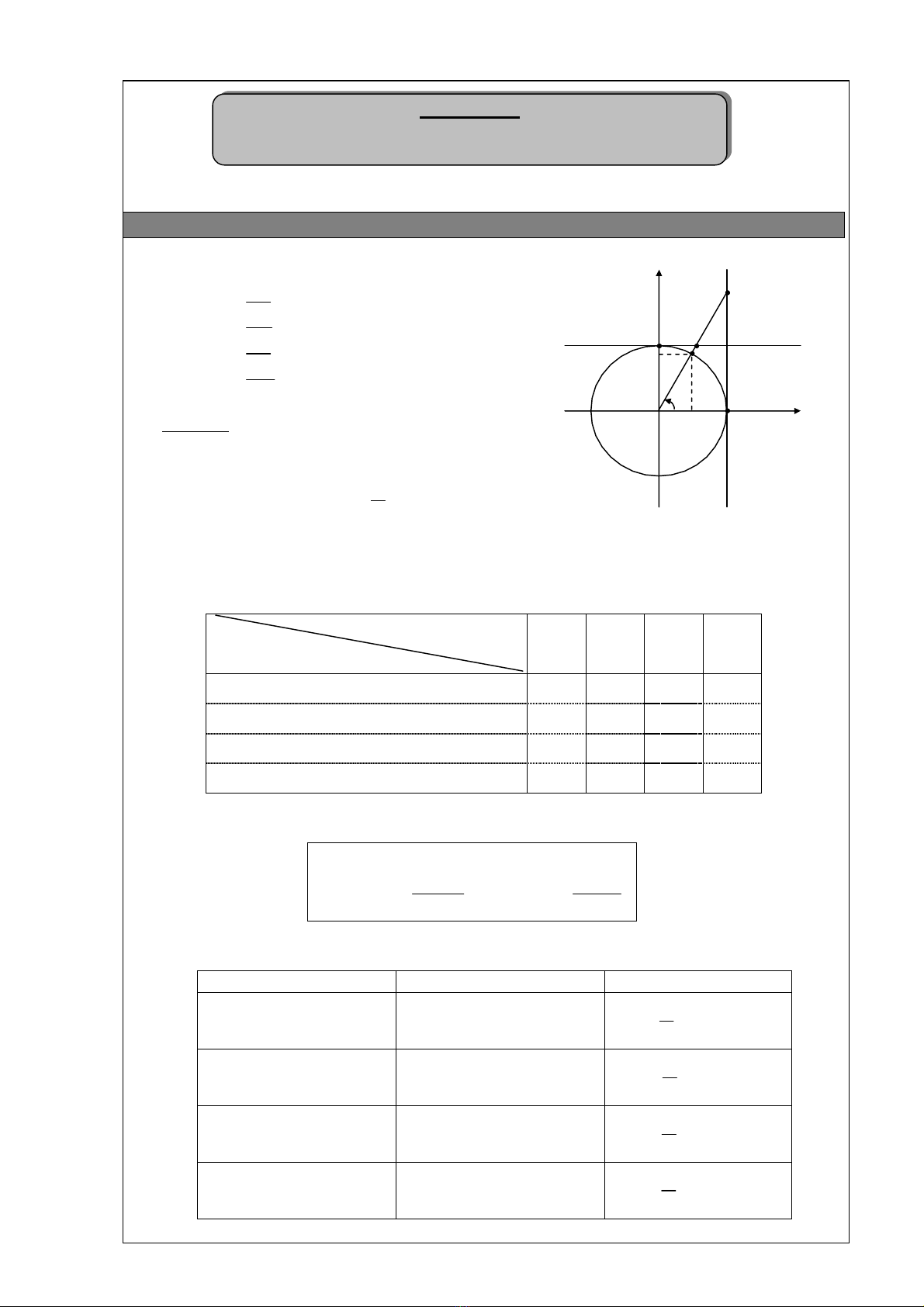
1. Định nghĩa các giá trị lượng giác:
OP
OQ
AT
BT
cos
sin
tan
'cot
a
a
a
a
=
=
=
=
Nhận xét:
·
aaa
"-££-££
· tana xác định khi
kkZ
,
2
p
ap
¹+Î
· cota xác định khi
kkZ
,
ap
¹Î
2. Dấu của các giá trị lượng giác:
Cung phần tư
Giá trị lượng giác
I II II IV
sin
a
+ + – –
cos
a
+ – – +
tan
a
+ – + –
cot
a
+ – + –
3. Hệ thức cơ bản:
sin2
a
+ cos2
a
= 1; tana.cota = 1
22
22
11
1tan;1cot
cossin
aa
aa
+=+=
4. Cung liên kết:
Cung đối nhau Cung bù nhau Cung phụ nhau
cos()cos
aa
-=
sin()sin
paa
-=
sincos
2
p
aa
æö
-=
ç÷
èø
sin()sin
aa
-=-
cos()cos
paa
-=-
cossin
2
p
aa
æö
-=
ç÷
èø
tan()tan
aa
-=-
tan()tan
paa
-=-
tancot
2
p
aa
æö
-=
ç÷
èø
cot()cot
aa
-=-
cot()cot
paa
-=-
cottan
2
p
aa
æö
-=
ç÷
èø
CHƯƠNG 0
CÔNG THỨC LƯỢNG GIÁC
cosin
O
cotang
sin
tang
p
A
M
Q
B
T'
a
T
Đại số 11 Trần Sĩ Tùng
Trang 2
5. Bảng giá trị lượng giác của các góc (cung) đặc biệt
II. CÔNG THỨC CỘNG
Công thức cộng:
Cung hơn kém
p
Cung hơn kém
2
p
sin()sin
paa
+=-
sincos
2
p
aa
æö
+=
ç÷
èø
cos()cos
paa
+=-
cossin
2
p
aa
æö
+=-
ç÷
èø
tan()tan
paa
+=
tancot
2
p
aa
æö
+=-
ç÷
èø
cot()cot
paa
+=
cottan
2
p
aa
æö
+=-
ç÷
èø
0
6
p
4
p
3
p
2
p
2
3
p
3
4
p
p
3
2
p
2
p
00 300 450 600 900 1200 1350 1800 2700 3600
sin 0
1
2
2
2
3
2
1
3
2
2
2
0 –1 0
cos 1
3
2
2
2
1
2
0
1
2
-
2
2
- –1 0 1
tan 0
3
3
1
3
3
-
–1 0 0
cot
3
1
3
3
0
3
3
- –1 0
sin()sin.cossin.cos
ababba
+=+
sin()sin.cossin.cos
ababba
-=-
cos()cos.cossin.sin
ababab
+=-
cos()cos.cossin.sin
ababab
-=+
tantan
tan()
1tan.tan
ab
ab
ab
+
+=
-
tantan
tan()
1tan.tan
ab
ab
ab
-
-=
+
Hệ quả: 1tan1tan
tan,tan
41tan41tan
papa
aa
aa
æöæö
+-
+=-=
ç÷ç÷
-+
èøèø
Trần Sĩ Tùng Đại số 11
Trang 3
III. CÔNG THỨC NHÂN
1. Công thức nhân đôi:
sin22sin.cos
aaa
=
2222
cos2cossin2cos112sin
aaaaa
=-=-=-
2
2
2tancot1
tan2;cot2
2cot
1tan
aa
aa
a
a
-
==
-
2. Công thức biểu diễn sina, cosa, tana theo t =
tan
2
a
:
Đặt:
tk
tan(2)
2
a
app
=¹+ thì:
t
t
2
2
sin
1
a
=
+
;
t
t
2
2
1
cos
1
a
-
=
+
;
t
t
2
2
tan
1
a
=
-
IV. CÔNG THỨC BIẾN ĐỔI
1. Công thức biến đổi tổng thành tích:
2. Công thức biến đổi tích thành tổng:
1
cos.coscos()cos()
2
1
sin.sincos()cos()
2
1
sin.cossin()sin()
2
ababab
ababab
ababab
éù
=-++
ëû
éù
=--+
ëû
éù
=-++
ëû
coscos2cos.cos
22
abab
ab
+-
+=
coscos2sin.sin
22
abab
ab
+-
-=-
sinsin2sin.cos
22
abab
ab
+-
+=
sinsin2cos.sin
22
abab
ab
+-
-=
sin()
tantan
cos.cos
ab
ab
ab
+
+=
sin()
tantan
cos.cos
ab
ab
ab
-
-=
sin()
cotcot
sin.sin
ab
ab
ab
+
+=
ba
ab
ab
sin()
cotcot
sin.sin
-
-=
sincos2.sin2.cos
44
pp
aaaa
æöæö
+=+=-
ç÷ç÷
èøèø
sincos2sin2cos
44
pp
aaaa
æöæö
-=-=-+
ç÷ç÷
èøèø
Công thức hạ bậc Công thức nhân ba (*)
2
2
2
1cos2
sin 2
1cos2
cos 2
1cos2
tan
1cos2
a
a
a
a
a
a
a
-
=
+
=
-
=+
3
3
3
2
sin33sin4sin
cos34cos3cos
3tantan
tan3 13tan
aaa
aaa
aa
a
a
=-
=-
-
=
-
Đại số 11 Trần Sĩ Tùng
Trang 4
Vấn đề 1: TẬP XÁC ĐỊNH, TẬP GIÁ TRỊ, TÍNH CHẴN – LẺ, CHU KỲ
sin
yx
=
: Tập xác định D = R; tập giá trị
1,1
T
éù
=-
ëû
; hàm lẻ, chu kỳ 0
2
T=
p
.
* y = sin(ax + b) có chu kỳ 0
2
T
a
=
p
* y = sin(f(x)) xác định
()
fx
Û
xác định.
cos
yx
=
: Tập xác định D = R; Tập giá trị
1,1
T
éù
=-
ëû
; hàm chẵn, chu kỳ 0
2
T=
p
.
* y = cos(ax + b) có chu kỳ 0
2
T
a
=
p
* y = cos(f(x)) xác định
()
fx
Û
xác định.
tan
yx
=
: Tập xác định \,
2
DRkkZ
ìü
=+Î
íý
îþ
pp
; tập giá trị T = R, hàm lẻ, chu kỳ 0
T
=
p
.
* y = tan(ax + b) có chu kỳ 0
T
a
=
p
* y = tan(f(x)) xác định
()
fx
Û
()
2
kkZ
¹+Î
p
p
cot
yx
=
: Tập xác định
{
}
\,
DRkkZ
=Î
p
; tập giá trị T = R, hàm lẻ, chu kỳ 0
T
=
p
.
* y = cot(ax + b) có chu kỳ 0
T
a
=
p
* y = cot(f(x)) xác định
()()
fxkkZ
Û¹Î
p
.
* y = f1(x) có chu kỳ T1 ; y = f2(x) có chu kỳ T2
Thì hàm số 12
()()
yfxfx
=± có chu kỳ T0 là bội chung nhỏ nhất của T1 và T2.
CHÖÔNG I
HAØM SOÁ LÖÔÏNG GIAÙC – PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
I. HÀM SỐ LƯỢNG GIÁC
Trần Sĩ Tùng Đại số 11
Trang 5
Baøi 1. Tìm tập xác định và tập giá trị của các hàm số sau:
a) 2
sin
1
x
yx
æö
=
ç÷
-
èø
b)
sin
yx
= c)
2sin
yx
=-
d)
2
1cos
yx
=- e) 1
sin1
yx
=
+
f) tan
6
yx
æö
=-
ç÷
èø
p
g) cot
3
yx
æö
=+
ç÷
èø
p
h) sin
cos()
x
yx
=
-
p
i) y = 1
tan1
x
-
Baøi 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y =
2sin1
4
x
æö
++
ç÷
èø
p
b)
2cos13
yx
=+-
c)
sin
yx
=
d) 2
4sin4sin3
yxx
=-+
e) 2
cos2sin2
yxx
=++
f) 42
sin2cos1
yxx
=-+
g) y = sinx + cosx h) y =
3sin2cos2
xx
- i) y =
sin3cos3
xx
++
Baøi 3. Xét tính chẵn – lẻ của hàm số:
a) y = sin2x b) y = 2sinx + 3 c) y = sinx + cosx
d) y = tanx + cotx e) y = sin4x f) y = sinx.cosx
g) y =
sintan
sincot
xx
xx
-
+ h) y =
3
3
cos1
sin
x
x
+
i) y =
tan
x
Baøi 4. Tìm chu kỳ của hàm số:
a)
sin2
yx
=
b)
cos
3
x
y= c)
2
sin
yx
=
d)
sin2cos
2
x
yx=+ e)
tancot3
yxx
=+
f)
32
cossin
57
xx
y=-
g)
2sin.cos3
yxx
=
h) 2
cos4
yx
= i) y = tan(-3x + 1)
HD: a)
p
b)
6
p
c)
p
d)
4
p
e)
p
f)
70
p
g)
p
h)
4
p
i)
3
p
Vấn đề 2: ĐỒ THỊ CỦA HÀM SỐ LƯỢNG GIÁC
1) Vẽ đồ thị hàm số lượng giác:
– Tìm tập xác định D.
– Tìm chu kỳ T0 của hàm số.
– Xác định tính chẵn – lẻ (nếu cần).
– Lập bảng biến thiên trên một đoạn có độ dài bằng chu kỳ T0 có thể chọn:
0
0,
xT
éù
Î
ëû
hoặc
00
,
22
TT
x
éù
Î-
êú
ëû
.
– Vẽ đồ thị trên đoạn có độ dài bằng chu kỳ.
– Rồi suy ra phần đồ thị còn lại bằng phép tịnh tiến theo vectơ
vkTi
0
..
=
r
r
về bên trái và
phải song song với trục hoành Ox (với
i
r
là véc tơ đơn vị trên trục Ox).