1
Bé gi¸o dôc vµ ®µo t¹o kú thi tuyÓn sinh ®¹i häc, cao ®¼ng n¨m 2002
------------------------- §¸p ¸n vµ thang ®iÓm ®Ò thi chÝnh thøc
M«n to¸n, khèi b
C©u ý Néi dung §H C§
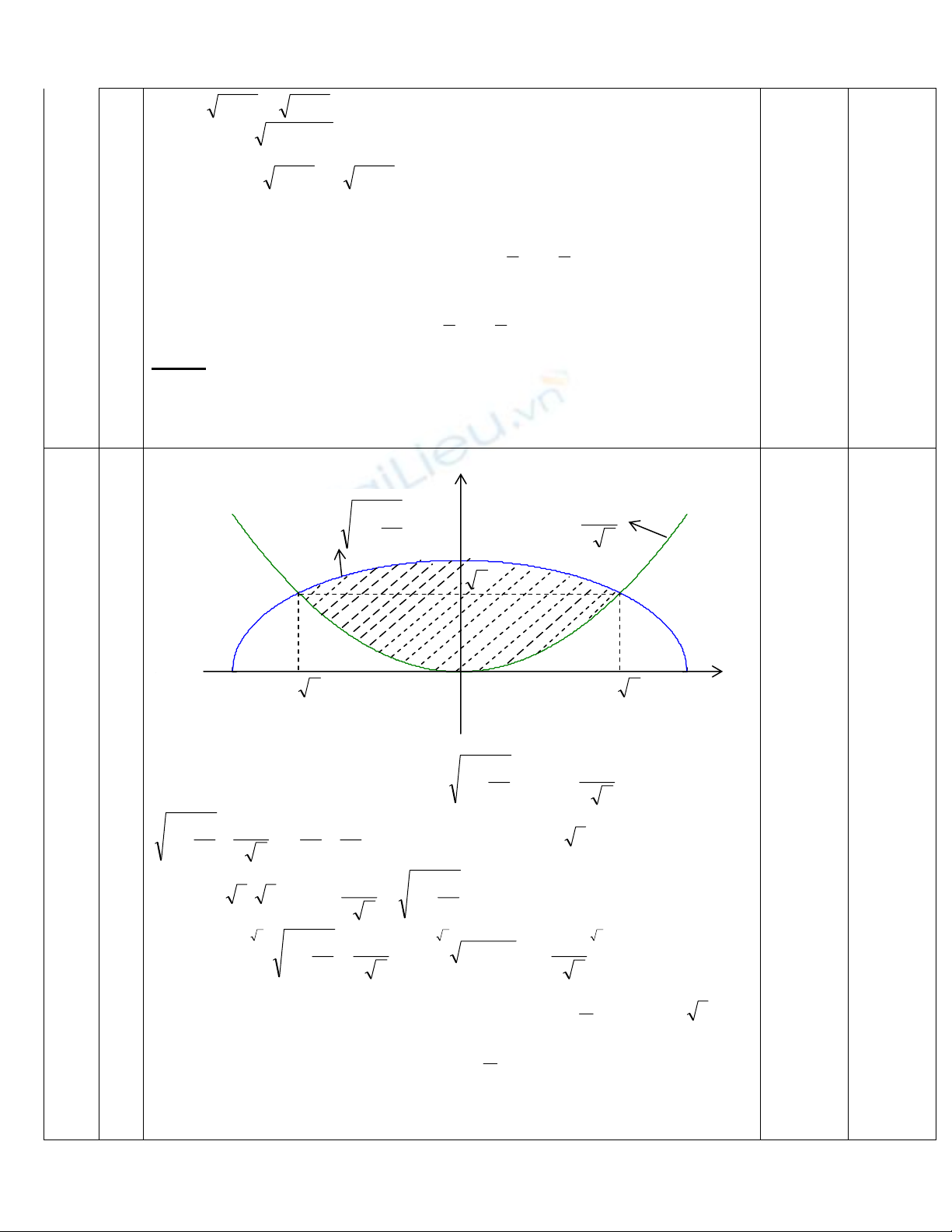
I 1 Víi 1=m ta cã 108 24 +−= xxy lµ hµm ch½n ⇒ ®å thÞ ®èi xøng qua Oy .
TËp x¸c ®Þnh ∀Rx ∈,
(
)
44164' 23 −=−= xxxxy , 0'
=
y
±=
=
⇔2
0
x
x
,
3
4
121612" 22
−=−= xxy 3
2
0" ±=⇔= xy .
B¶ng biÕn thiªn:
∞+
−
−∞− 2
3
2
0
3
2
2x
−'y 0
+
0
−
0+
"y +0
−
0
+
∞+ 10 ∞+
y lâm U C§ U lâm
CT låi CT
6− 6
−
Hai ®iÓm cùc tiÓu :
()
6;2
1−−A vµ
(
)
6;2
2
−
A.
Mét ®iÓm cùc ®¹i:
()
10;0B.
Hai ®iÓm uèn:
−
9
10
;
3
2
1
U vµ
9
10
;
3
2
2
U.
Giao ®iÓm cña ®å thÞ víi trôc tung lµ
(
)
10;0B.
§å thÞ c¾t trôc hoµnh t¹i 4 ®iÓm cã hoµnh ®é:
64 +±=x vµ 64 −±=x.
(ThÝ sinh cã thÓ lËp 2 b¶ng biÕn thiªn)
∑
0,1 ®
0,25 ®
0,5 ®
0,25 ®
∑
5,1 ®
0,5 ®
0,5 ®
0,5 ®
x 0
10
y
-6
-2 2
A2
A1
B
U1 U2
2
I 2
(
)
(
)
922924' 2223 −+=−+= mmxxxmmxy ,
=−+
=
⇔= 092
0
0' 22 mmx
x
y
Hµm sè cã ba ®iÓm cùc trÞ ⇔ ph−¬ng tr×nh 0'
=
y cã 3 nghiÖm
ph©n biÖt (khi ®ã 'y ®æi dÊu khi qua c¸c nghiÖm)
⇔
ph−¬ng tr×nh
092 22 =−+ mmx cã 2 nghiÖm ph©n biÖt kh¸c 0.
092 22 =−+ mmx
−
=
≠
⇔
m
m
x
m
2
9
02
2. Ph−¬ng tr×nh 092 22 =−+ mmx
cã 2 nghiÖm kh¸c 0
<<
−<
⇔.30
3
m
m
VËy hµm sè cã ba ®iÓm cùc trÞ
<<
−<
⇔.30
3
m
m
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
II 1
xxxx 6cos5sin4cos3sin 2222 −=−
2
12cos1
2
10cos1
2
8cos1
2
6cos1 xxxx
+
−
−
=
+
−
−
⇔
()()
06cos8cos10cos12cos
=
+
−+⇔ xxxx
()
07cos11coscos =−⇔ xxx
02sin9sincos =⇔ xxx
.
2
9
02sin9sin Zk
k
x
k
x
xx ∈
=
=
⇔=⇔
π
π
Chó ý:
ThÝ sinh cã thÓ sö dông c¸c c¸ch biÕn ®æi kh¸c ®Ó ®−a vÒ ph−¬ng tr×nh tÝch.
∑
0,1 ®
0,25 ®
0,25 ®
0,5 ®
∑
0,1 ®
0,25 ®
0,25 ®
0,5 ®
2
(
)
1)729(loglog 3≤−
x
x (1).
§iÒu kiÖn: 73log1729
0)729(log
0729
1,0
9
3
>⇔>−⇔
>−
>−
≠>
x
xx
x
x
x (2).
Do 173log9>>x nªn
(
)
x
x≤−⇔ 729log)1( 3
(
)
072333729 2≤−−⇔≤−⇔ xxxx (3).
§Æt x
t3= th× (3) trë thµnh
293898072
2≤⇔≤≤−⇔≤≤−⇔≤−− xttt x.
KÕt hîp víi ®iÒu kiÖn (2) ta ®−îc nghiÖm cña bÊt ph−¬ng tr×nh lµ:
273log9
≤
<
x.
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
3
3
++=+
−=−
).2(2
)1(
3
yxyx
yxyx §iÒu kiÖn: )3(
.0
0
≥+
≥−
yx
yx
()
+=
=
⇔=−−−⇔ .1
01)1( 63
yx
yx
yxyx
Thay y
x
= vµo (2), gi¶i ra ta ®−îc .1
=
=
yx
Thay 1+= yx vµo (2), gi¶i ra ta cã: 2
1
,
2
3== yx .
KÕt hîp víi ®iÒu kiÖn (3) hÖ ph−¬ng tr×nh cã 2 nghiÖm:
1,1 =
=
yx vµ 2
1
,
2
3== yx
Chó ý:
ThÝ sinh cã thÓ n©ng hai vÕ cña (1) lªn luü thõa bËc 6 ®Ó di ®Õn kÕt qu¶:
+=
=
.1yx
yx
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
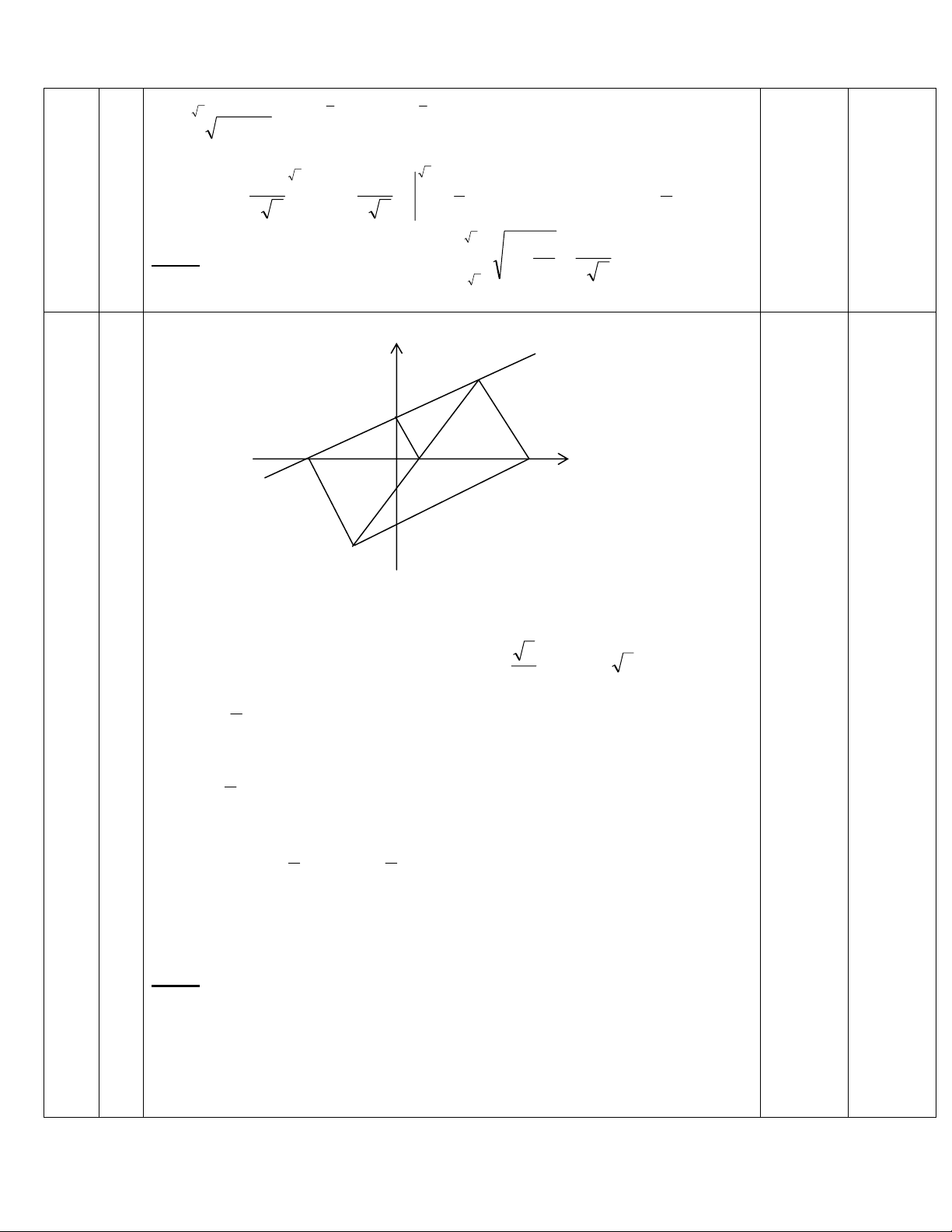
III
T×m giao ®iÓm cña hai ®−êng cong 4
4
2
x
y−= vµ 24
2
x
y=:
4
4
2
x
−=24
2
x8804
432
2
24
±=⇔=⇔=−+⇔ xx
xx .
Trªn
[
]
8;8− ta cã 24
2
x
4
4
2
x
−≤ vµ do h×nh ®èi xøng qua trôc tung
nªn dx
xx
S∫
−−=
8
0
22
24
4
42 21
8
0
2
8
0
2
22
1
16 SSdxxdxx −=−−= ∫∫ .
§Ó tÝnh 1
S ta dïng phÐp ®æi biÕn tx sin4
=
, khi 4
0
≤≤ t th× 80 ≤≤ x.
tdtdx cos4= vµ
∈∀> 4
;00cos
π
tt . Do ®ã
∑
0,1 ®
0,25 ®
0,25 ®
∑
5,1 ®
0,5 ®
0,25 ®
x
0
-4 4
2
y
-2 2 22
2A2
A1
4
x
4y
2
−= 24
x
y
2
=
4
()
422cos18cos1616
4
0
4
0
2
8
0
2
1+=+==−= ∫∫∫
π
ππ
dtttdtdxxS .
3
8
26
1
22
18
0
3
8
0
2
2=== ∫xdxxS . VËy 3
4
2
21 +=−=
π
SSS .
Chó ý: ThÝ sinh cã thÓ tÝnh diÖn tÝch dx
xx
S∫
−
−−=
8
8
22
24
4
4 .
0,25 ®
0,25 ®
0,5 ®
0,25 ®
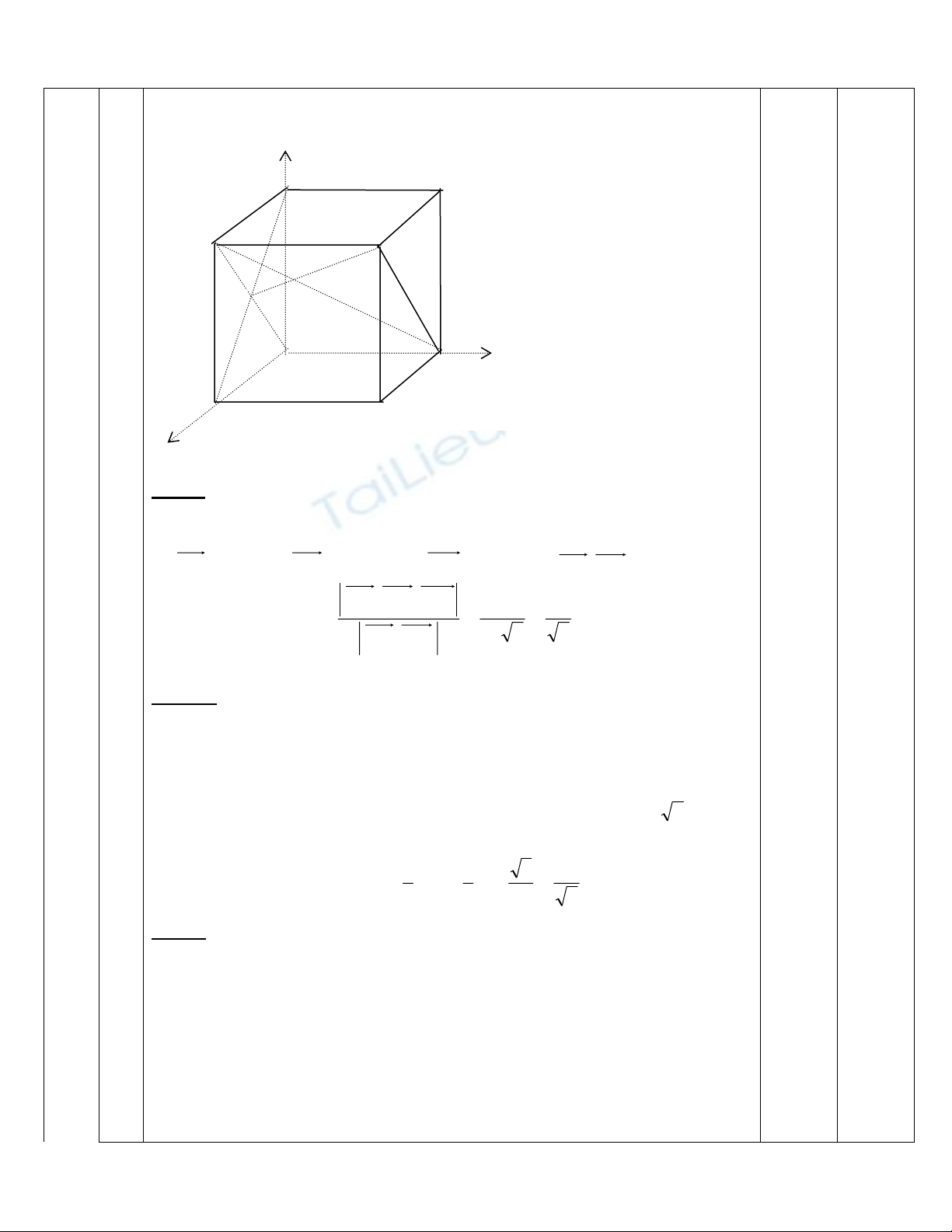
IV 1
Kho¶ng c¸ch tõ
I
®Õn ®−êng th¼ng AB b»ng 2
55=⇒ AD vµ
2
5
== IBIA .
Do ®ã BA,lµ c¸c giao ®iÓm cña ®−êng th¼ng
A
B víi ®−êng trßn t©m
I
vµ b¸n
kÝnh 2
5
=
R. VËy täa ®é BA, lµ nghiÖm cña hÖ :
=+
−
=+−
2
2
2
2
5
2
1
022
yx
yx
Gi¶i hÖ ta ®−îc
()()
2;2,0;2 BA − (v× 0
<
A
x)
()( )
2;1,0;3 −−⇒ DC .
Chó ý:
ThÝ sinh cã thÓ t×m täa ®é ®iÓm
H
lµ h×nh chiÕu cña
I
trªn ®−êng th¼ng AB .
Sau ®ã t×m BA, lµ giao ®iÓm cña ®−êng trßn t©m
H
b¸n kÝnh HA víi ®−êng
th¼ng AB .
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑
5,1 ®
0,25 ®
0,5 ®
0,5 ®
0,25 ®
x
C
I
O
A
D
B
H
y
5
IV 2a) T×m kho¶ng c¸ch gi÷a BA1vµ DB1.
C¸ch I. Chän hÖ täa ®é §ªcac vu«ng gãc Oxyz sao cho
()()()()
(
)
(
)
(
)( )
aaDaaaCaaBaaCaAaDaBA ;;0,;;;;0;;0;;;0;0,0;;0,0;0;,0;0;0 1111 ⇒
() ()()
0;0;,;;,;0; 1111 aBAaaaDBaaBA =−−=−=⇒ vµ
[
]
(
)
222
11 ;2;, aaaDBBA =.
VËy
()
[
]
[]
66
,
.,
,2
3
11
1111
11
a
a
a
DBBA
BADBBA
DBBAd === .
C¸ch II.
()
DBBADCABBA
ADBA
ABBA
11111
1
11 ⊥⇒⊥⇒
⊥
⊥.
T−¬ng tù DBCA 111 ⊥
(
)
111 BCADB ⊥⇒ .
Gäi
()
111 BCADBG ∩= . Do aCBBBAB
=
=
=
11111 nªn
GGCGBGA ⇒== 11 lµ t©m tam gi¸c ®Òu 11 BCA cã c¹nh b»ng 2a.
Gäi Ilµ trung ®iÓm cña BA1 th× IG lµ ®−êng vu«ng gãc chung cña BA1 vµ
DB1, nªn
()
6
2
3
3
1
3
1
,1111
a
BAICIGDBBAd ==== .
Chó ý:
ThÝ sinh cã thÓ viÕt ph−¬ng tr×nh mÆt ph¼ng
(
)
Pchøa BA1 vµ song song víi
DB1 lµ: 02 =−++ azyx vµ tÝnh kho¶ng c¸ch tõ 1
B(hoÆc tõ D) tíi
()
P,
hoÆc viÕt ph−¬ng tr×nh mÆt ph¼ng
(
)
Q chøa DB1 vµ song song víi BA1 lµ:
022 =−++ azyx vµ tÝnh kho¶ng c¸ch tõ 1
A(hoÆc tõ B) tíi
(
)
Q.
∑
0,1 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
0,25 ®
∑
5,1 ®
0,25 ®
0,5 ®
0,25 ®
0,5 ®
0,25 ®
0,5 ®
0,5 ®
x
D
1
D
C
1
B
1
A
1
z
y
x
A
C
B
I
G