ĐÁP ÁN NGÂN HÀNG CÂU HỎI THI CỦA CÁC HỌC PHẦN ĐÀO TẠO THEO HỆ THỐNG TÍN CHỈ KỸ THUẬT ĐO LƯỜNG 1a

Chia sẻ: HQ Hải Quân Computer | Ngày: | Loại File: PDF | Số trang:49

Thêm vào BST

Báo xấu

170
lượt xem 46
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

CÂU HỎI LOẠI 1 (2 ĐIỂM) 1. Trình bày sơ đồ cấu trúc thiết bị đo kiểu so sánh. Đáp án: 1.1. cấu trúc thiết bị đo kiểu so sánh (0,5 điểm) Trong thiết bị đo kiểu so sánh đại lượng vào x thường được biến đổi thành đại lượng trung gian yx qua một phép biến đổi T: yx= T.x Sau đó yx được so sánh với đại lượng bù yk . Có: ∆y = y x − y k Có thể căn cứ vào thao tác so sánh để phân loại các phương pháp đo khác nhau. 1.2....

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: ĐÁP ÁN NGÂN HÀNG CÂU HỎI THI CỦA CÁC HỌC PHẦN ĐÀO TẠO THEO HỆ THỐNG TÍN CHỈ KỸ THUẬT ĐO LƯỜNG 1a

TRƯỜNG ĐẠI HỌC KỸ THUẬT CÔNG NGHIỆP CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM KHOA ĐIỆN TỬ ĐỘC LẬP – TỰ DO – HẠNH PHÚC Bộ môn: Đo lường & ĐKTĐ Thái nguyên ngày tháng năm 2008 ĐÁP ÁN NGÂN HÀNG CÂU HỎI THI CỦA CÁC HỌC PHẦN ĐÀO TẠO THEO HỆ THỐNG TÍN CHỈ KỸ THUẬT ĐO LƯỜNG 1a 1. Mã số học phần: 40251 2. Số tín chỉ:03 3. Ngành (chuyên ngành ) đào tạo: Kỹ thuật điện, SPKT điện 4. Nội dung đáp án: 4.1. CÂU HỎI LOẠI 1 (2 ĐIỂM) 1. Trình bày sơ đồ cấu trúc thiết bị đo kiểu so sánh. Đáp án: 1.1. cấu trúc thiết bị đo kiểu so sánh (0,5 điểm) Trong thiết bị đo kiểu so sánh đại lượng vào x thường được biến đổi thành đại lượng trung gian yx qua một phép biến đổi T: yx= T.x Sau đó yx được so sánh với đại lượng bù yk . Có: ∆y = y x − y k Có thể căn cứ vào thao tác so sánh để phân loại các phương pháp đo khác nhau. 1.2. Phân loại phương pháp đo căn cứ vào điều kiện cân bằng (0,75 điểm) a) Phương pháp so sánh kiểu cân bằng(Hình 1.4) Trong phương pháp này, đại lượng vào so sánh: yx = const ; đại lượng bù yk = const Tại điểm cân bằng : ∆y = yx- yk → 0 b) Phương pháp so sánh không cân bằng (Hình 1.5) Cũng giống như trường hợp trên song ∆y → ε ≠ 0 1
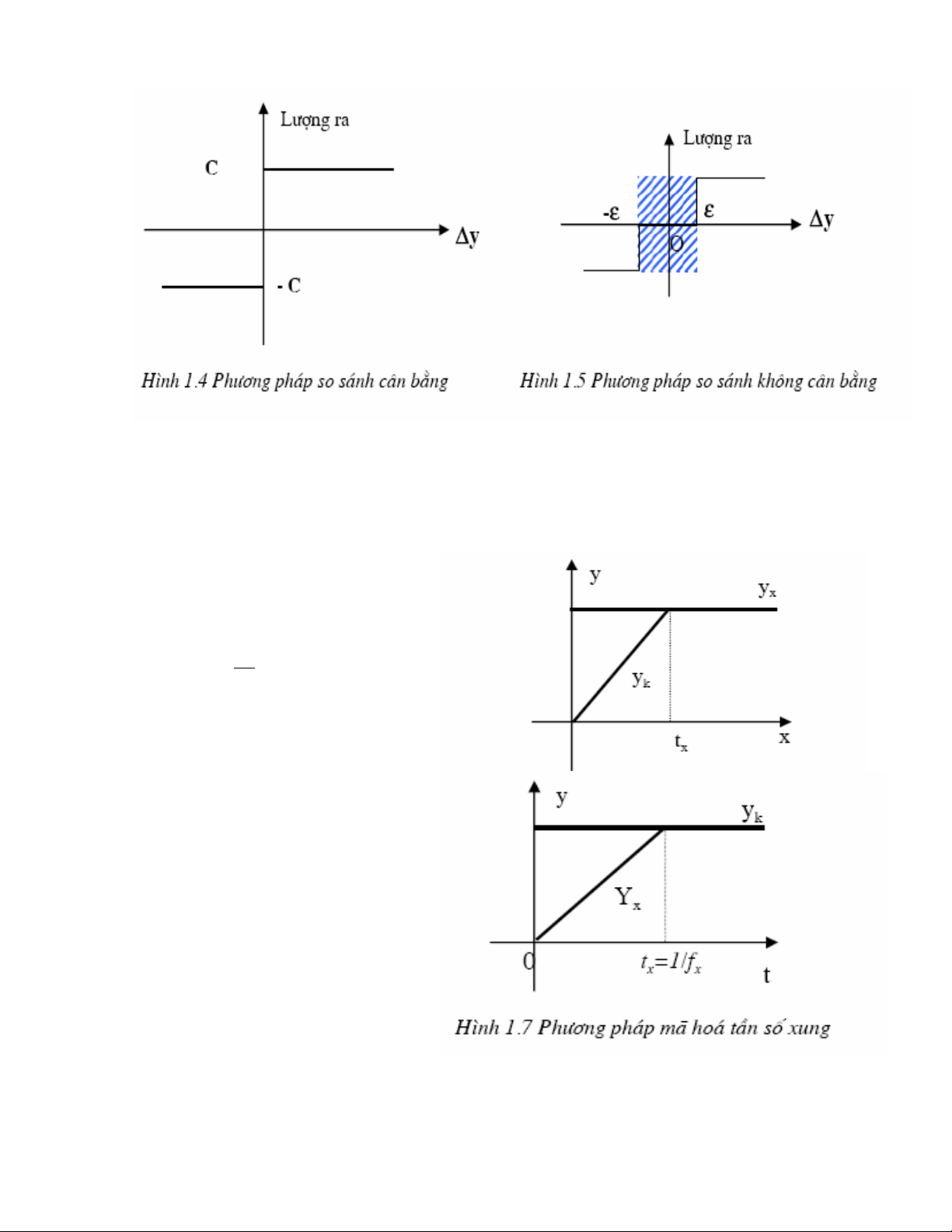
1.3. Phân loại phương pháp đo căn cứ vào cách tạo điện áp bù (0,75 điểm) a) Phương pháp mã hoá thời gian Trong phương pháp này đại lượng vào yx= const còn đại lượng bù yk cho tăng tỉ lệ với thời gian t: yk= y0.t (y0= const) Tại thời điểm cân bằng yx = yk = y0 .tx yx → tx = y0 Đại lượng cần đo yx được biến thành khoảng thời gian tx Ở đây phép so sánh phải thực hiện một bộ ngưỡng ⎧1 ∆y = sign( y x − yk ) = ⎨ ⎩0 y x≥ yk y x < yk b) Phương pháp mã hoá tần số xung. - Trong phương pháp này đại lượng vào yx cho tăng tỉ lệ với đại lượng cần đo x và khoảng thời gian t: yx = t.x, còn đại lượng bù yk được giữ không đổi. Tại điểm cân bằng có: 2
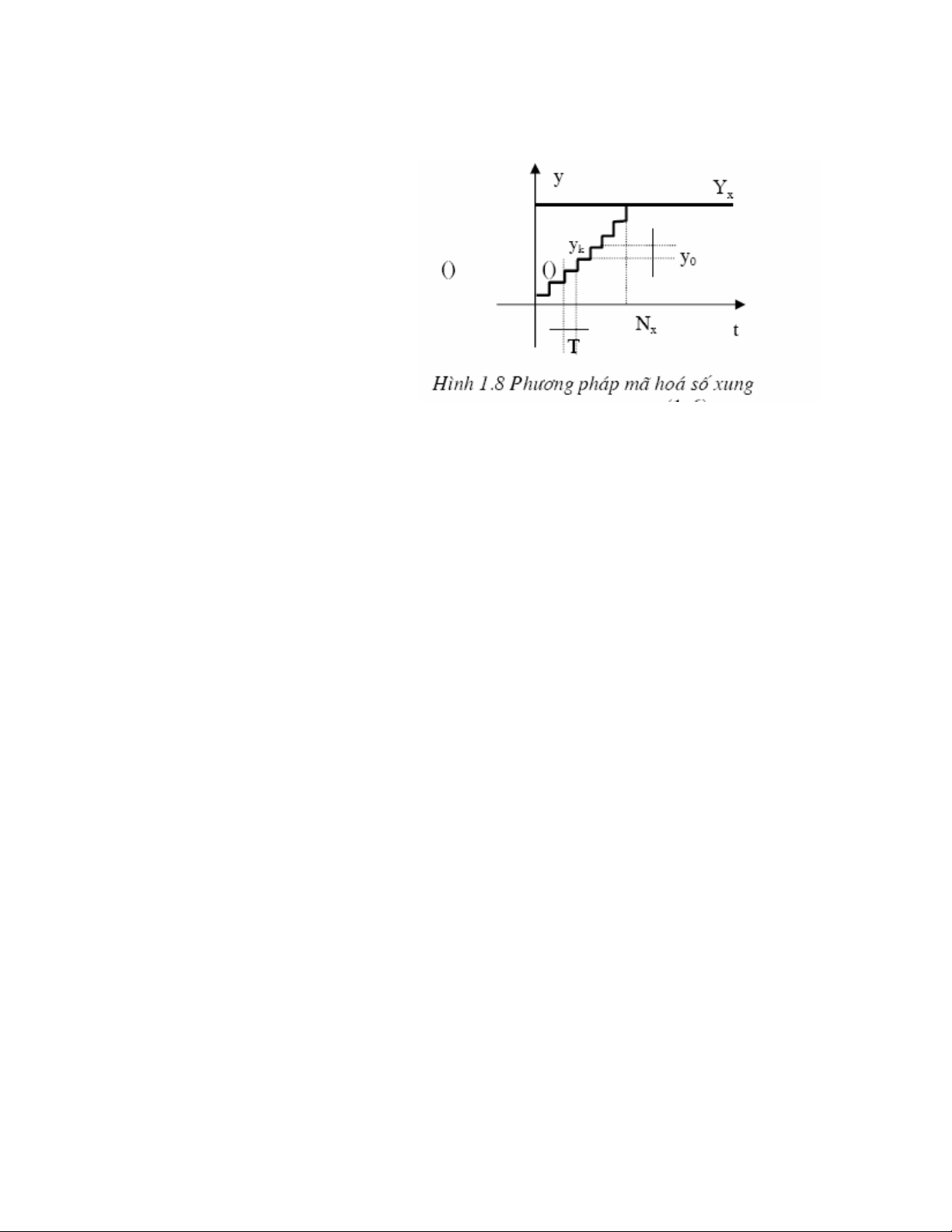
yx=x.tx= yk=const Suy ra fx = 1/tx = x/yk. Đại lượng cần đo x đã được biến thành tần số fx. Ở đây phép so sánh cũng phải thực hiện một bộ ngưỡng . ⎧1 yk ≥ y x ∆y = sign( y x − yk ) = ⎨ ⎩0 yk < y x c) Phương pháp mã hoá số xung Trong phương pháp này đại lượng vào yx=const, còn đại lượng bù yk cho tăng tỉ lệ với thời gian t theo quy luật bậc thang với những bước nhảy không đổi yo gọi là bước lượng tử. T=const gọi là xung nhịp. n Ta có: Yk = yo ∑1(t − iT ) i =1 Tại điểm cân bằng đại lượng vào yx được biến thành số xung Nx. yx= Nx . y0 Sai số của phương pháp này là không lớn hơn một bước lượng tử . Để xác định được điểm cân bằng, phép so sánh cũng phải thực hiện một bộ ngưỡng ⎧1 y x ≥ yk ∆y = sign( y x − yk ) = ⎨ ⎩0 y x < yk 2. Sai số phụ là gì, cho 2 ví dụ minh hoạ. Đáp án: 2.1. Sai số phụ:(1 điểm) 3
* Thiết bị đo phải thu năng lượng từ đối tượng đo dưới bất kì hình thức nào để biến thành đại lượng đầu ra của thiết bị. Tiêu thụ năng lượng thể hiện ở phản tác dụng của thiết bị đo lên đối tượng đo gây ra những sai số mà ta thường biết được nguyên nhân gọi là sai số phụ về phương pháp. Trong khi ®o ta cè g¾ng phÊn ®Êu sao cho sai sè nµy kh«ng lín h¬n sai sè c¬ b¶n cña thiÕt bÞ. Tæn hao n¨ng l−îng víi m¹ch ®o dßng ¸p lµ: ∆PA= RA. I2. ∆PU = U2/ RV. VËy ta t¹m tÝnh sai sè phô do ¶nh h−ëng cña tæng trë vµo lµ: γI= RA / Rt ; γU = Rt / RV. RA: §iÖn trë cña ampemet hoÆc phÇn tö ph¶n øng víi dßng RV: §iÖn trë cña v«nmÐt hoÆc phÇn tö ph¶n øng víi ¸p Rt: §iÖn trë t¶i. 2.2.Ví dụ minh họa (Mỗi ví dụ được 0,5 điểm). 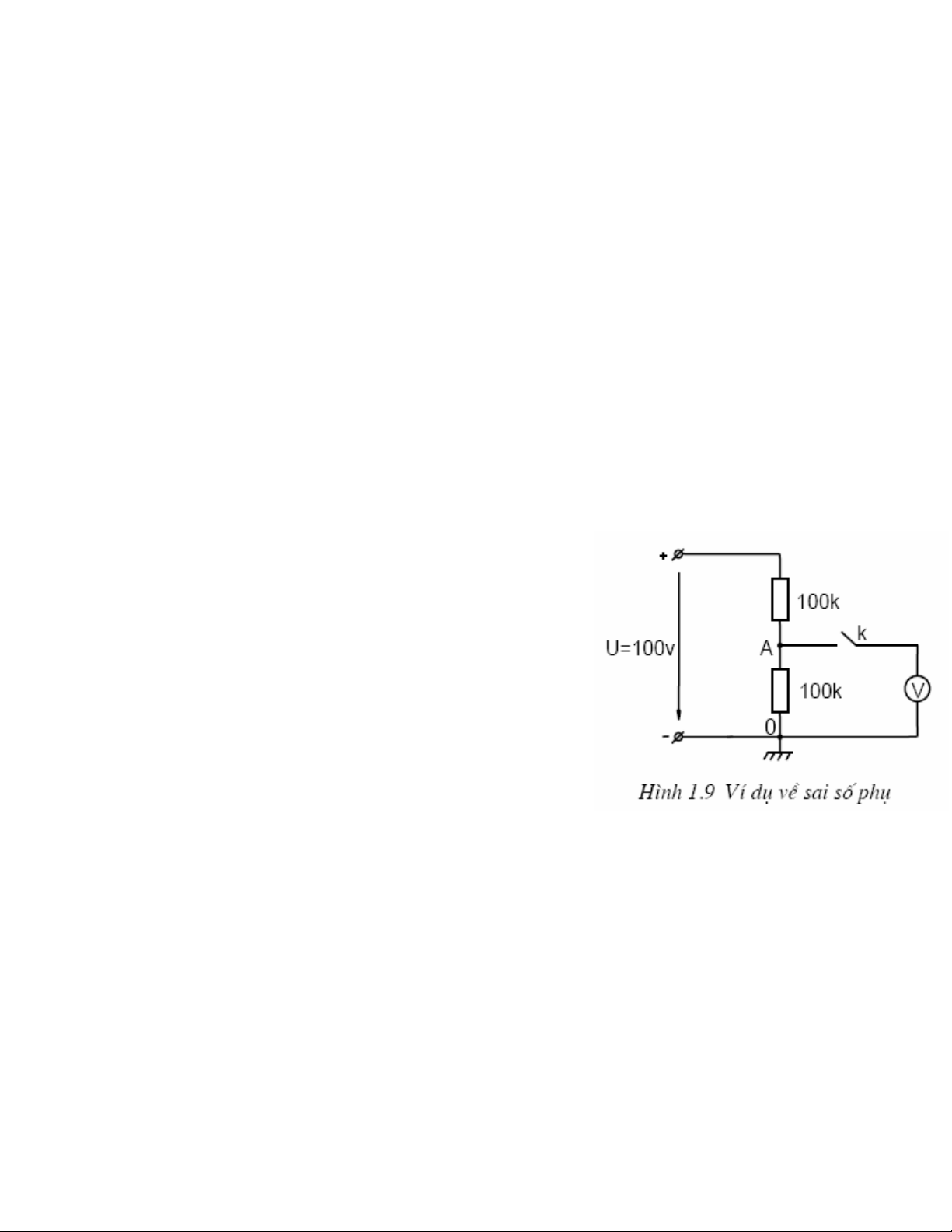2.2.1 Ví dụ 1 : Phân tích sai số phụ khi đo áp trên hình 1.9. Xét mạch điện như hình vẽ - Giả sử cần kiểm tra điện áp UAO Theo lý lịch [ UAO ]= 50±2 (V) - Xác định điện áp trên R2 khi không có Volmet (K mở) và khi có Volmet (K đóng): + Xét khi chưa đo (K mở), ta có ngay: UAO = 50 (V) + Xét khi đo (K đóng). Giả sử RV = 100 kΩ. Vậy điện áp đo được: 4
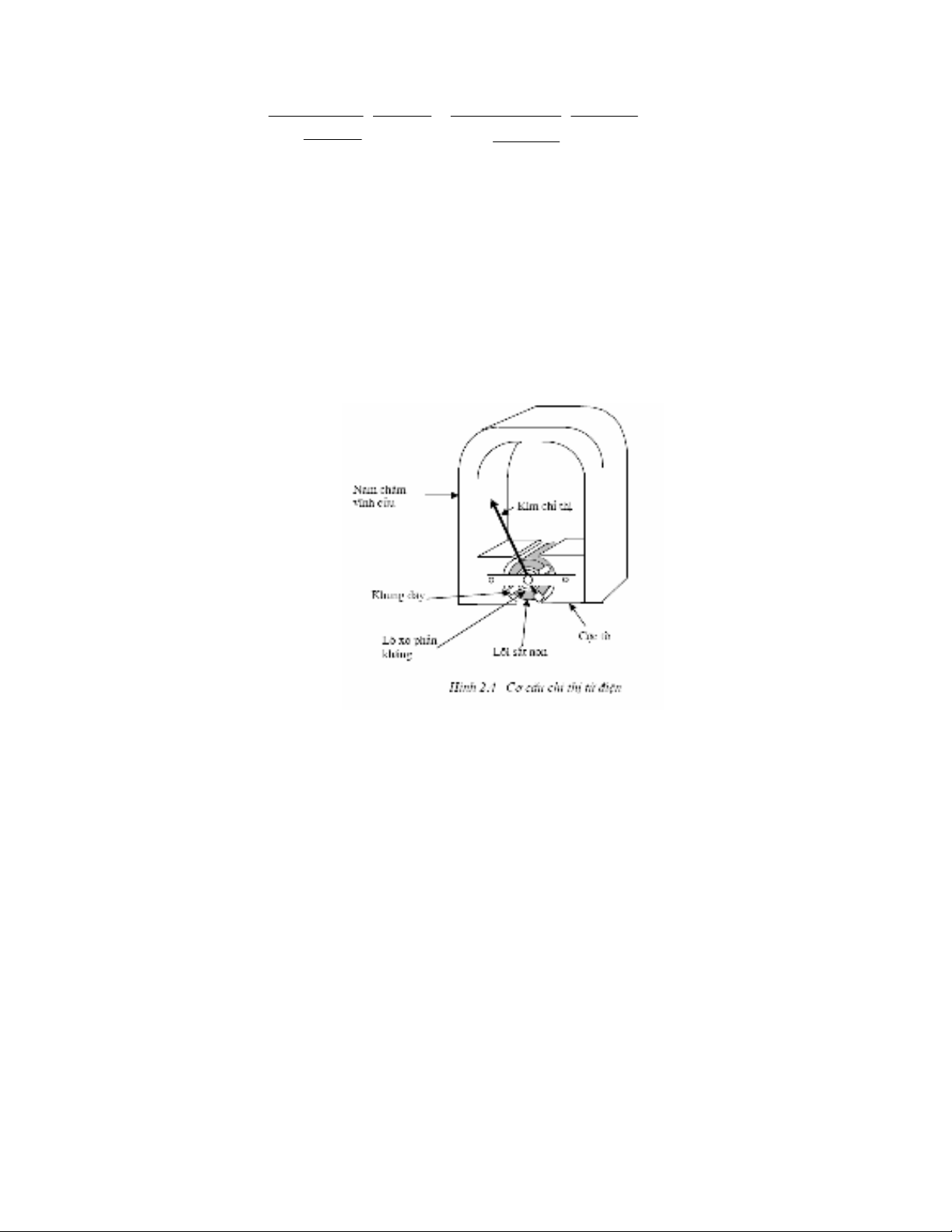
U RR 100 105.105 UV = U AO ' = ⋅ 2 V = ⋅ = 33,3(V ) R2 RV R2 + RV 10 5 .10 5 10 5 + 10 5 R1 + 10 + 5 5 R2 + RV 10 + 105 Vậy điện áp UAO sai số từ 33,3 (V) lên 50 (V) chính là sai số phụ về phương pháp do ảnh hưởng của Volmet sinh ra. 3. Trình bày nguyên lý làm việc của cơ cấu đo từ điện. Đáp án: 3.1. Loại cơ cấu có một khung dây động (1 điểm) 1. Hình vẽ (0,5 điểm) 2. Nguyên lý làm việc (0,5 điểm) Khi ta cho dòng điện một chiều I chạy vào khung dây, dưới tác dụng của từ trường nam châm vĩnh cửu trong khe hở không khí, các cạnh của khung dây sẽ chịu tác dụng một lực điện từ có trị số xác định theo biểu thức: F = BlWI Trong đó: B là trị số cảm ứng từ trong khe hở không khí l là Chiều dài tác dụng của khung dây W là số vòng dây I là trị số dòng điện - Ta thấy 2 cạnh của khung dây cùng chịu tác dụng của lực F nhưng ngược chiều nhau nên sẽ tạo ra mômen quay Mq quay khung dây lệch khỏi vị trí ban đầu một góc α. Mq được tính theo biểu thức: 5
d Mq = 2 F = BldWI = BSWI 2 d: Kích thước ngang của khung dây S = d .l : diện tích bề mặt khung dây Khi khung dây quay thì lò xo phản sẽ sinh ra mômen phản được tính: Mp = D. α Trong đó D là hệ số phản kháng phụ thuộc vào tính chất vật lý của lò xo. Dưới tác động đồng thời của hai mômen quay và mômen phản, phần động của cơ cấu sẽ dừng lại ở vị trí cân bằng: BSW Mq = Mp Ù BSWI=D α Ù α = .I = S I . I D B.S .W Ở đây S I = = const là độ nhạy của cơ cấu theo dòng điện. D Ta thấy α tỉ lệ bậc nhất với I. Vậy từ góc quay ta xác định được dòng điện cần đo 3.2.loại cơ cấu có hai khung dây động(Logomet từ điện) (1 điểm) 1. Hình vẽ (0,5 điểm) 2. Nguyên lý làm việc (0,5 điểm) Khi ta cho các dòng một chiều I1, I2 chạy vào các cuộn dây động. Dưới tác dụng của từ trường nam châm vĩnh cửu sẽ tạo ra các mô men quay M1, M2 với: M1 = B1S1W1I1. M2 = B2S2W2I2. Vì khe hở không khí là không đều cho nên cảm ứng từ B phụ thuộc vị trí của khung dây động: B1 = f1 (α ) Æ M1 = f1 (α ) S1W1I1; B2= f2 (α ) --> M2 = f 2 (α ) .S2W2 I2. 6
Vì không có lò xo phản nên phần động sẽ cân bằng khi M1 = M2. Ta có: f1 (α ) S1W1I1 = f 2 (α ) .S2W2 I2 f1 (α )S1W1 I 2 Vậy = f 2 (α )S 2W2 I1 ⎛I ⎞ Giải phương trình này ta tìm được quan hệ: α = f ⎜⎜ 2 ⎟⎟ ⎝ I1 ⎠ 4. Trình bày nguyên lý làm việc của cơ cấu đo điện động. Đáp án: 4.1.Lo¹i cã mét khung d©y ®éng(1 điểm) 1. Hình vẽ (0,5 điểm) cuén d©y tÜnh cuén d©y ®éng H×nh 2.6 C¬ cÊu chØ thÞ ®iÖn ®éng 2. Nguyªn lý lµm viÖc(0,5 điểm) -XÐt khi cho c¸c dßng ®iÖn mét chiÒu I1 vµ I2 vµo c¸c cuén d©y phÇn tÜnh vµ ®éng, trong lßng cuén d©y tÜnh sÏ tån t¹i mét tõ tr−êng. Tõ tr−êng nµy sÏ t¸c ®éng lªn dßng ®iÖn ch¹y trong cuén d©y ®éng vµ t¹o ra m« men quay: : dWe Mq = dα N¨ng l−îng tõ tr−êng tÝch luü trong lßng cuén d©y lµ: 1 1 We = L1 I12 + L 2 I 22 + M12 I1I 2 2 2 7
Trong ®ã L1, L2 lµ ®iÖn c¶m cña c¸c cuén d©y vµ chóng kh«ng phô thuéc vµo gãc quay α. M12 lµ hç c¶m cña hai cuén d©y, M12 thay ®æi khi phÇn ®éng quay. dWe dM12 M« men quay Mq = = I1 I 2 dα dα - XÐt khi hai dßng ®iÖn ®−a vµo c¸c cuén d©y lµ dßng ®iÖn xoay chiÒu th×: dM12 Mq(t) = i1 i 2 dα gi¶ sö i1 = I1msinωt vµ i2 =I2msin(ωt-Ψ) Do phÇn ®éng cã qu¸n tÝnh mµ kh«ng kÞp thay ®æi theo gi¸ trÞ tøc thêi cho nªn thùc tÕ lÊy theo gi¸ trÞ trung b×nh trong mét chu kú: T T 1 1 dM 12 dM 12 Mq = To∫ M q (t )dt = T0 ∫ I1m I 2 m sin ωt sin(ωt −ψ ) dα dt = dα I 1 I 2 cosψ Víi ψ lµ gãc lÖch pha gi÷a hai dßng ®iÖn; I1, I2 lµ c¸c gi¸ trÞ hiÖu dông cña dßng ®iÖn lÇn l−ît ch¹y trong c¸c cuén d©y tÜnh vµ ®éng. Tãm l¹i, trong mäi tr−êng hîp ta ®Òu cã: dM 12 Mq = I1 I 2 cosψ = K .I1 .I 2 . cosψ dα dM 12 Khi Mq = Mp ⇒ I 1 I 2 cosψ = Dα dα 1 dM 12 VËy α = I1 I 2 cosψ = K1 .I1 .I 2 . cosψ D dα Lo¹i cã hai khung d©y ®éng hay l«g«mÐt ®iÖn ®éng(1 điểm) Đáp án: 1. Hình vẽ (0,5 điểm) Cuén d©y tÜnh Nam ch©m vÜnh Khung d©y ®éng 2. Nguyªn lÝ lµm viÖc i Khi cho hai dßng ®iÖn xoay chiÒu i, i1, i2 lÇn l−ît ch¹y vµo cuén d©y tÜnh vµ c¸c cuén d©y ®éng, trong lßng cuén d©y tÜnh sÏ cã mét tõ tr−êng. Tõ tr−êng nµy i1 i2 sÏ t¸c ®éng lªn dßng ®iÖn ch¹y trong c¸c cuén d©y ®éng sinh ra c¸c m« men Mq1, H×nh 2.7 L«g«mÐt ®iÖn ®éng Mq2. 8
dM 1 ⎛∗ ∗ ⎞ M q1 = I .I1 cos⎜ I , I1 ⎟ dα ⎝ ⎠ dM 2 ⎛∗ ∗ ⎞ M q2 = I .I 2 cos⎜ I , I 2 ⎟ dα ⎝ ⎠ Víi M1, M2 lµ hÖ sè hç c¶m gi÷a cuén d©y tÜnh vµ lÇn l−ît c¸c cuén d©y ®éng. Ng−êi ta bè trÝ sao cho c¸c m«men nµy ng−îc chiÒu nhau, vËy khi c©n b»ng phÇn ®éng, ta cã Mq1 = Mq2 dM 1 ⎛ ∗ ∗ ⎞ dM 2 ⎛∗ ∗ ⎞ I .I 1 cos⎜ I , I 1 ⎟ = I .I 2 cos⎜ I , I 2 ⎟ dα ⎝ ⎠ dα ⎝ ⎠ dM 1 ⎛∗ ∗ ⎞ I 2 cos⎜ I , I 2 ⎟ → dα = ⎝ ⎠ dM 2 ⎛ ∗ ∗ ⎞ dα I 1 cos⎜ I , I 1 ⎟ ⎝ ⎠ ⎛ I cos β 2 ⎞ Gi¶i ph−¬ng tr×nh trªn, ta ®−îc: α = f ⎜⎜ 2 ⎟⎟ ⎝ I1 cos β1 ⎠ Víi I1, I2 lµ c¸c gi¸ trÞ hiÖu dông cña c¸c dßng ®iÖn i1, i2; β1, β2 lµ gãc lÖch pha gi÷a dßng ®iÖn i , i1 vµ i , i2 5. Trình bày mạch biến đổi từ cơ số 10 sang chỉ thị 7 thanh Đáp án: §Çu vµo lµ c¸c sè tù nhiªn tõ 0 ÷ 9, ®Çu ra lµ chØ thÞ b¶y thanh b»ng ®ièt ph¸t quang. XuÊt ph¸t tõ thùc tÕ ta cã b¶ng tr¹ng th¸i nh− sau (1 điểm): B¶ng 2.2 B¶ng tr¹ng th¸i biÕn ®æi tõ sè nhÞ ph©n sang thËp ph©n Tr¹ng th¸i c¸c phÇn tö Sè thËp ph©n Y1 Y2 Y3 Y4 Y5 Y6 Y7 0 (X0) 1 1 1 1 1 1 0 1 (X1) 0 1 1 0 0 0 0 2 (X2) 1 1 0 1 1 0 1 3 (X3) 1 1 1 1 0 0 1 4 (X4) 0 1 1 0 0 1 1 5 (X5) 1 0 1 1 0 1 1 6 (X6) 1 0 1 1 1 1 1 7 (X8) 1 1 1 0 0 0 0 9
8 (X8) 1 1 1 1 1 1 1 9 (X9) 1 1 1 1 0 1 1 Tõ b¶ng tr¹ng th¸i ta cã thÓ viÕt ®−îc ph−¬ng tr×nh nh− sau (víi sè thø tù c¸c thanh nh− phÇn tr−íc) (1 điểm) Y1 = X0 + X2 +X3 + X5 + X6 +X7 + X8 + X9 Y2 = X0 +X1+ X2 +X3 +X4+X7 + X8 + X9 Y3 = X0 + X1 +X3 +X4+ X5 + X6 +X7 + X8 + X9 Y4 = X0 + X2 +X3 + X5 + X6 + X8 + X9 Y5 = X0 + X2 + X6 + X8 Y6 = X0 + X4+ X5 + X6 + X8 + X9 Y7 = X2 +X3 +X4+ X5 + X6 + X8 + X9 Tõ ®©y ta cã thÓ thiÕt lËp m¹ch logic sau: X0 X2 X4 X6 X8 X1 X3 X5 X7 X9 Y1 OR Y2 OR OR Y3 Y4 OR H×nh 2.18 M¹ch biÕn ®æi tõ Y5 m· thËp ph©n sang chØ thÞ 7 thanh OR Y6 OR Y7 OR 6. Tính toán sai số ngẫu nhiên với số lần đo có hạn (n ≤ 30 ).(2 điểm) 10
Đáp án: Quá trình gia công được tiến hành theo các bước như sau: + Bước1: Tính giá trị trung bình Kỳ vọng toán học được lấy là trung bình cộng của n lần đo. n ∑ xi M [x ] = x = x d = k =1 n + Bước 2: Xác định các sai số dư _ δ i = xi − x ; i = 1n + Bước 3: Độ lệch bình quân phương của đại lượng đo ∑ ( x − x) n n 2 2 n ⎛ n xi ⎞ i ∑δ i 2 ∑ ⎜ x i − ∑ ⎟ i =1 ⎝ i =1 n ⎠ σx = i =1 = i =1 = n −1 n −1 n −1 + Bước 4: Xác định độ lệch bình quân phương trung bình đại số Nếu ta lấy kết quả là giá trị trung bình của n lần đo thì phương sai sẽ giảm đi n lần ∑ ( x − x) n 2 n σx i ∑δ i 2 σx = = i =1 = i =1 n n ( n − 1) n −1 + Bước 5: Sai số ngẫu nhiên được tính: ∆x = kst. σ x Trong đó: kst là hệ số Student, nó phụ thuộc vào số lần thu thập n và xác suet yêu cầu p. Hệ số kst được tra trong sổ tay kỹ thuật: kst = f(n,p) + Bước 6 : Kết quả đo được tính 2 n ⎛ 1 n ⎞ ∑x ∑ ⎜ i n ∑ xi ⎟ i =1 ⎝ x − i =1 ⎠ x = x ± ∆x = i ± kst n n ( n − 1) Chú ý: Trong thực tế có những lần thu thập số liệu cho kết quả không đáng tin cậy (và ta thường gọi là nhiễu của tập số liệu). Ta phải loại bỏ lần đo này nhờ thuật toán sau: Sau khi tính σ ta so sánh các δ i với 3 σ với i=1 đến n, nếu lần đo nào có δ i ≥ 3δ thì 11
phải loại bỏ lần đo đó và tính lại từ đầu với ( n-1) phép đo còn lại. Có thể chứng minh rằng việc loại bỏ đó đã đảm bảo độ tin cậy 99,7%. 7. Tính toán sai số gián tiếp, cho ví dụ. Đáp án: 7.1. Tính toán sai số gián tiếp(1 điểm) Gi¶ sö cã 1 phÐp ®o gi¸n tiÕp ®¹i l−îng y th«ng qua c¸c phÐp ®o trùc tiÕp x1,x2,..xn y = f (x1,x2,…xn) ∂y ∂y ∂y Ta cã: dy = dx1 + dx2 + ... dxn ∂x ∂x ∂x Sai sè tuyÖt ®èi cña phÐp ®o gi¸n tiÕp ®−îc ®¸nh gi¸ 2 2 n ⎛ 2 2 ⎛ ∂y ⎞ ⎛ ∂y ⎞ ⎛ ∂y ⎞ ∂y ⎞ ∆y = ⎜ ∆x1 ⎟ + ⎜ ∆x2 ⎟ + ... + ⎜ ∆xn ⎟ = ∑ ⎜ ∆xk ⎟ (1 − 20) ⎝ ∂x1 ⎠ ⎝ ∂x2 ⎠ ⎝ ∂xn ⎠ ∂x k =1 ⎝ k ⎠ ∆x1, ∆x2, …∆xn: sai sè tuyÖt ®èi cña phÐp ®o c¸c ®¹i l−îng trùc tiÕp x1, x2,…xn. Sai sè t−¬ng ®èi cña phÐp ®o gi¸n tiÕp ®−îc tÝnh lµ: 2 2 2 2 ∆y ⎛ ∆x ⎞ ⎛ ∂y ⎞ ⎛ ∆x ⎞ ⎛ ∂y ⎞ γy = = ⎜⎜ 1 ⎟⎟ ⎜⎜ ⎟⎟ + ... + ⎜⎜ n ⎟⎟ ⎜⎜ ⎟⎟ = γ 2x1 + γ 2x 2 + ... + γ 2x n y ⎝ y ⎠ ⎝ ∂x 1 ⎠ ⎝ y ⎠ ⎝ ∂x n ⎠ Trong ®ã: γx1, γx2, …, γxn lµ sai sè t−¬ng ®èi cña c¸c phÐp ®o trùc tiÕp x1, x2,…,xn B¶ng 1.2 B¶ng tÝnh sai sè tuyÖt ®èi vµ sai sè t−¬ng ®èi cña 1 sè hµm y th−êng gÆp Sai sè t−¬ng ®èi Hµm y Sai sè tuyÖt ®èi ∆y γ y = ∆y / y (∆x1 )2 + (∆x 2 )2 x1 + x2 ± (∆x1 ) 2 + (∆x 2 ) 2 ± (x1 + x 2 ) 2 2 2 ⎛ ∆x ⎞ ⎛ ∆x ⎞ ± x (∆x 2 ) + x (∆x 1 ) ± ⎜⎜ 1 ⎟⎟ + ⎜⎜ 2 ⎟⎟ 2 2 2 2 x1.x2 1 2 ⎝ x1 ⎠ ⎝ x 2 ⎠ x 12 (∆x 2 ) + x 22 (∆x 1 ) 2 2 2 2 x1 ⎛ ∆ x ⎞ ⎛ ∆x ⎞ ± ± ⎜⎜ 1 ⎟⎟ + ⎜⎜ 2 ⎟⎟ x2 x 42 ⎝ x1 ⎠ ⎝ x 2 ⎠ ⎛ ∆x ⎞ xn ± nx n−1∆x ± n⎜ ⎟ ⎝ x ⎠ 12
7.2. VÝ dô (1 điểm) Ng−êi ta sö dông AmpemÐt vµ VolmÐt ®Ó ®o ®iÖn trë b»ng ph−¬ng ph¸p gi¸n tiÕp. AmpemÐt cã thang ®o lµ 1A, cÊp chÝnh x¸c lµ 1. VolmÐt cã thang ®o lµ 150V, cÊp chÝnh x¸c 1.5. Khi ®o ta ®−îc sè chØ cña hai ®ång hå lµ: I = 1A, U =100V H·y tÝnh sai sè tuyÖt ®èi vµ t−¬ng ®èi cña phÐp ®o ®iÖn trë trªn. Bµi lµm + Sai sè tuyÖt ®èi cña AmpemÐt lµ: ∆I = DI γ% = 1. 1/100 = 0.01(A) + Sai sè tuyÖt ®èi cña VolmÐt lµ: ∆U = Duγ% = 150.1.5/100=2.25(V) + Gi¸ trÞ ®iÖn trë theo phÐp ®o lµ: R = U/I =100/1 =100(Ω) + Sai sè tuyÖt ®èi cña phÐp ®o ®iÖn trë lµ: I 2 ∆U 2 + U 2 ∆I 2 1 * 2.25 2 + 100 2 * 0.012 ∆R = ± = ± = 2.46Ω I4 1 + Sai sè t−¬ng ®èi cña phÐp ®o ®iÖn trë 2 2 ∆R ⎛ ∆U ⎞ ⎛ ∆I ⎞ γ =± 100 = ± ⎜ ⎟ + ⎜ ⎟ *100 = R ⎝ U ⎠ ⎝ I ⎠ 2 2 ⎛ 2.25 ⎞ ⎛ 0.01 ⎞ ± ⎜ ⎟ +⎜ ⎟ *100 = ±0.024 *100 = 2.4% ⎝ 100 ⎠ ⎝ 1 ⎠ 13
8. Trình bày nguyên lý làm việc của cơ cấu đo cảm ứng. Đáp án: 8.1.Hình vẽ (1 điểm). Ix2 Ix1 M21 M12 F2 F1 H×nh 2.11 C¬ cÊu chØ thÞ c¶m øng 8.2.Nguyªn lý lµm viÖc(1 điểm) Khi cho dßng ®iÖn i1 vµo cuén d©y 1 th× cuén d©y 1 t¹o ra tõ th«ng φ1 xuyªn qua ®Üa nh«m, dßng ®iÖn i2 vµo trong cuén d©y 2 t¹o ra tõ th«ng φ2 còng xuyªn qua ®Üa nh«m. Tõ th«ng φ1 c¶m øng trªn ®Üa nh«m søc ®iÖn ®éng e1 chËm pha h¬n φ1 mét gãc π/2. Tõ th«ng φ2 c¶m øng trªn ®Üa nh«m søc ®iÖn ®éng e2 chËm pha h¬n φ2 mét gãc π/2. V× ®Üa nh«m ®−îc coi nh− rÊt nhiÒu vßng d©y ®Æt s¸t nhau, cho nªn E1, E2 sÏ t¹o ra trªn ®Üa nh«m c¸c dßng ®iÖn xo¸y ix1 vµ ix2 chËm pha h¬n so víi e1 vµ e2 c¸c gãc α1 vµ α2 v× ngoµi ®iÖn trë thuÇn cßn cã thµnh phÇn c¶m øng, tuy nhiªn do c¸c thµnh phÇn c¶m øng ®ã rÊt nhá nªn ta gi¶ thiÕt c¸c gãc α1 vµ α1 ≈ 0 Do cã sù t−¬ng hç gi÷a tõ th«ng φ1, φ2 víi c¸c dßng ®iÖn ix1 vµ ix2 mµ sinh ra c¸c lùc F1 vµ F2 vµ c¸c m« men t−¬ng øng lµm quay ®Üa nh«m φ1 Ta xÐt c¸c m«men thµnh phÇn nh− sau: φ2 M11 lµ m«men sinh ra do φ1 t¸c ®éng lªn ix1 I2 I1 M12 lµ m«men sinh ra do φ1 t¸c ®éng lªn ix2 ϕ M21 lµ m«men sinh ra do φ2 t¸c ®éng lªn ix1 γ1 Ix1 M22 lµ m«men sinh ra do φ2 t¸c ®éng lªn ix2 E1 Gi¸ trÞ tøc thêi cña m«men quay M1t do sù Ix2 t¸c ®éng t−¬ng hç gi÷a φ1 vµ dßng tøc thêi ix1 lµ: E2 H×nh 2.12 §å thÞ vect¬ 14
M1t = Cφ1ix1 C: lµ hÖ sè tû lÖ Gi¶ sö: φ1 =φ1m sinωt, ix1 =Ix1m sin(ωt - γ), víi γ lµ gãc lÖch pha gi÷a φ1 vµ ix1 M1t = Cφ1mIx1m sinωt sin(ωt - γ) V× phÇn ®éng cã qu¸n tÝnh cho nªn ta cã m«men lµ ®¹i l−îng trung b×nh trong mét chu kú T. T T 1 1 M = ∫ M 1t dt = ∫ Cφ1m I x1m sin ωt sin(ωt − γ )dt T0 T0 = Cφ1Ix1cosγ Ta xÐt lÇn l−ît c¸c m«men trªn M11 = C11φ1Ix1 cos (φ1, Ix1) = C11φ1Ix1 cos (π/2) = 0 M12 = C12φ1Ix2 cos (φ1, Ix2) = C12φ1Ix2 cos (π/2 + ϕ ) = -C12φ1Ix2 sinϕ M21 = C21φ2Ix1 cos (φ2, Ix1) = C21φ2Ix1 cos (π/2-ϕ) = C21φ2Ix1sinϕ M22 = C22φ2Ix2 cos (φ2, Ix2) = C22φ2Ix2 cos (π/2) = 0 Nh− vËy m«men quay sÏ lµ tæng c¸c m«men thµnh phÇn: Mq = M12 + M21 M12 vµ M21 cã dÊu ng−îc nhau do vËy m«men tæng sÏ kÐo ®Üa nh«m vÒ mét phÝa duy nhÊt: Mq = - M12 + M21 = C12φ1Ix2 sinϕ + C21φ2Ix1sinϕ NÕu dßng ®iÖn t¹o ra φ1 vµ φ2 lµ h×nh sin vµ ®Üa nh«m lµ ®ång nhÊt(chØ cã ®iÖn trë thuÇn) th× c¸c dßng ®iÖn xo¸y Ix1 vµ Ix2 sÏ tû lÖ víi tÇn sè vµ tõ th«ng sinh ra nã Tøc lµ: Ix1 = C3fφ1, Ix2 =C4fφ2 Do vËy Mq = C12φ1 C4 f φ2 sinϕ + C21φ2 C3fφ1 sinϕ = (C12C4 + C21C3) fφ1φ2 sinϕ = Cfφ1φ2sinϕ Víi C = C12C4 + C21C3 lµ h»ng sè cña c¬ cÊu chØ thÞ c¶m øng trong ®Üa nh«m g©y tæn hao c«ng suÊt. 4.2. CÂU HỎI LOẠI 2 (2 ĐIỂM) 1. Yêu cầu về điện trở khi đo dòng và áp. Đáp án: 1.1.Khi ®o dßng ®iÖn (1 điểm) Sai sè phô trong qu¸ tr×nh ®o l−êng sÏ ®−îc tÝnh: 15
I-I A RA R γp = = ≈ A , v× RA A
Víi mét phô t¶i cã ®iÖn trë Rt ®Æt trong m¹ch cã ®iÖn trë nguån Rn , nÕu dïng volmet cÊp chÝnh x¸c γ (hoÆc ®é chÝnh x¸c yªu cÇu cña m¹ch lÊy tÝn hiÖu ¸p lµ γ) th× ®iÖn trë cña volmet ph¶i ®¶m b¶o ®iÒu kiÖn sao cho γP ≤ γ, hay ta cã: R0 Rv ≥ ; γ NÕu kh«ng ®¶m ®iÒu kiÖn trªn, sai sè phô do volmet g©y ra lín h¬n sai sè cña b¶n th©n c¬ cÊu chØ thÞ vµ ta ph¶i dïng c«ng thøc hiÖu chØnh. Ut = (1 + γp) Uv 2. Các phương pháp mở rộng giới hạn đo khi đo dòng điện. Đáp án: 2.1.§èi víi AmpemÐt mét chiÒu(1 điểm) §iÖn trë sun ®−îc m¾c song song víi c¬ cÊu ®o nh− h×nh vÏ 3.7 (Shunt = rÏ nh¸nh) Is Rs Ta cã: I = I0 + Is I I0 Rs R = ⇒ Is = 0 I0 Is R0 Rs I0 R0 ⎛ R ⎞ Tõ ®ã ta cã: I = I 0 ⎜1 + 0 ⎟ = I 0 K I ⎝ Rs ⎠ H×nh3.7 Ph−¬ng ph¸p më réng thang ®o cho AmpemÐt mét chiÒu R0 Víi KI = 1 + , gäi lµ hÖ sè ph©n dßng cña AmpemÐt. Rs Khi biÕt R0, dßng ®iÖn ®Þnh møc lÖch toµn thang ®o I0, dßng cÇn ®o I, ta cã thÓ tÝnh ®−îc: I R0 Cùc ¸p KI = ⇒ Rs = (3-5) I0 KI −1 2.2.§èi víi AmpemÐt xoay chiÒu (1 điểm) Cùc dßng a. Ph−¬ng ph¸p chia nhá cuén d©y H×nh 3.8 17
I W W W W W W 2I W W W W 4I W W H×nh 3.9 Ph−¬ng ph¸p chia nhá cuén d©y a. Ph−¬ng ph¸p dïng biÕn dßng ®iÖn Ta cã: I1W1 ≈ I2W2 I1 W1 BI Hay I1/I2 = W2/W1 = KI , KI gäi lµ hÖ sè m¸y biÕn dßng W2 Th«ng th−êng, ®Ó dÔ rµng cho viÖc chÕ I2 t¹o vµ sö dông W1 chØ cã mét vßng, øng víi dßng ®iÖn I1 ë chÕ ®é ®Þnh møc theo mét d·y A sè −u tiªn nµo ®ã; W2 nhiÒu vßng h¬n øng H×nh 3.10 S¬ ®å dïng BI ®Ó ®o dßng ®iÖn víi dßng I2 ë chÕ ®é ®Þnh møc lµ: I2®m = 1 A hoÆc I2®m = 5 A VD: M¸y biÕn dßng : 100/5 ; 200/5; 300/ 5… 3. Các phương pháp mở rộng giới hạn đo khi đo điện áp. Đáp án: 3.1.Ph−¬ng ph¸p dïng ®iÖn trë phô (1 điểm) R0 Rp Víi: R0 ®iÖn trë cña c¬ cÊu ®o Rp lµ ®iÖn trë phô U0 ®iÖn ¸p ®Æt lªn c¬ cÊu U0 Ux ®iÖn ¸p cÇn ®o Ux Ta cã: U0 Ux U R0 + Rp H×nh3.13 Më réng thang ®o cho VolmÐt = ⇒ x = R0 R0 + Rp U0 R0 18
Ux R0 + Rp §Æt: Ku = ⇒ Ku = ⇒ KuR0 = R0 + Rp ⇒ Rp =R0 (Ku -1) U0 R0 Ux Ku : Gäi lµ hÖ sè më réng thang ®o: Ku = U0 VÝ dô: S¬ ®å ®iÖn cña 1 VolmÐt cã 3 giíi h¹n ®o U1(-) U2(-) U3(-) Rp1 Rp2 Rp3 H×nh 3.14 S¬ ®å volmÐt cã 3 thang ®o 3.2.Ph−¬ng ph¸p dïng biÕn ®iÖn ¸p (1 điểm) V× volmet cã ®iÖn trë lín nªn cã thÓ coi biÕn ®iÖn ¸p lu«n lµm viÖc ë chÕ ®é kh«ng t¶i: U1 W1 Ta cã: ≈ = KU U1 U 2 W2 §Ó tiÖn trong qu¸ tr×nh sö dông vµ chÕ t¹o W1 ng−êi ta quy −íc ®iÖn ¸p ®Þnh møc cña biÕn ®iÖn ¸p phÝa thø cÊp bao giê còng lµ 100V. Cßn phÝa W2 s¬ cÊp ®−îc chÕ t¹o t−¬ng øng víi c¸c cÊp cña ®iÖn ¸p l−íi. Khi l¾p hîp bé gi÷a biÕn ®iÖn ¸p vµ V VolmÐt ng−êi ta kh¾c ®é VolmÐt theo gi¸ trÞ ®iÖn ¸p phÝa s¬ cÊp H×nh 3.15 Dïng BU ®o ®iÖn ¸p lín Gièng nh− BiÕn dßng ®iÖn, biÕn ®iÖn ¸p lµ phÇn tö cã cùc tÝnh, cã cÊp chÝnh x¸c, vµ ph¶i ®ù¬c kiÓm ®Þnh tr−íc khi l¾p ®Æt 4. Trình bày nguyên lý làm việc của điện thế kế tự động tự ghi. Đáp án: 4.1.Sơ đồ tóm tắt nguyên lý (1điểm) Lo¹i nµy th−êng dïng ®o nhiÖt ®é lß t«i, ram, nhiÖt luyÖn,dïng nhËn d¹ng c¸c ®èi t−îng lµ lß gia nhiÖt - S¬ ®å tãm t¾t nguyªn lý nh− h×nh 3.23 B¨ng giÊy 1 19
H×nh 3.23 S¬ ®å nguyªn lý ®iÖn thÕ kÕ tù ®éng tù ghi 4.2.Qu¸ tr×nh ®o ®−îc chia lµm hai b−íc (1 điểm): *KiÓm tra ®é chÝnh x¸c cña c¸c ®iÖn ¸p mÉu t0 *Qu¸ tr×nh ®o nhiÖt ®é * Qu¸ tr×nh tù ghi t H×nh 3.24: KÕt qu¶ qu¸ tr×nh tù ghi 5.Nguyên lý làm việc của Volmet số chuyển đổi trực tiếp. Đáp án: 5.1VolmÐt sè chuyÓn ®æi trùc tiÕp kiÓu bï quÐt (1 điểm). 20