C©u I.
Cho m lµ mét sè nguyªn dû¬ng, h·y t×m cûåc trÞ cña hµm sè
y=x
m(4-x)
2.
Kh¶o s¸t sûå biÕn thiªn vµ vÏ ®å thÞ cña hµm sè khim=1.
C©u II.
1) ABC lµ mét tam gi¸c bÊt k×. Chûáng minh r»ng víi mäi sè x ta ®Òu cã
1+1
2x2³cosA + x(cosB + cosC).
2) Gi¶i phû¬ng tr×nh
cosx + 1
cosx +sinx+ 1
sinx =10
3.
C©u III.
1) Gi¶i vµ biÖn luËn theo a, b phû¬ng tr×nh
ax + b
x-a =x-b
x+a
.
2) Cho 3 sè a, b, c tháa m·n ®iÒu kiÖn a2+b
2+c
2=1.Chûáng minh r»ng:
abc+2(1+a+b+c+ab+ac+bc)≥0.
C©u IVa. 1) Chûáng tá r»ng hµm sè
F(x) = ()
xx−+ln 1
lµ mét nguyªn hµm trªn Rcña hµm sè f(x) = x
1+|x|
.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
_______________________________________________________________
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
_________________________________________________________
C©u I.
1) m1 2 m
y' mx (4 x) 2(4 x)x
−
=−−−=
m1
x (4 x)[4m (m 2)x]
−
=−−+
.
a) XÐt tr−êng hîp m ≥ 2. Khi ®ã ph−¬ng tr×nh y' = 0 cã ba nghiÖm 1
x0=, 2
4m
xm2
=+ vµ
3
x4=.
NÕu m − 1 ch½n (tøc m = 3, 5, 7, ...) th× y' sÏ cïng dÊu víi
(4 − x) [4m − (m + 2)x] vµ do ®ã : min
y(4)0= vµ
mm4
max 2 m2
m4
y(x) M
(m 2)
+
+
==
+.
NÕu m - 1 lÎ (tøc m = 2, 4, 6, ...) th× dÊu cña y' lµ dÊu cña
x(4 − x)[4m − (m + 2) x]
LËp b¶ng xÐt dÊu sÏ cã kÕt qu¶
min
y(0)0
= ; max 2
y(x)M
=, min
y(4)0
=
b) §Ò nghÞ b¹n ®äc tù lµm cho tr−êng hîp m = 1
2
(y x(4 x) )
=− .
2) Kh¶o s¸t, vÏ ®å thÞ hµm sè
2
yx(4x)
=−
dµnh cho b¹n ®äc.
C©u II.
1) 2
x2(cosBcosC)x2(1cosA)0−++−≥
. (1)
2
' (cosB cosC) 2(1 cosA)∆= + − − =
22 2
CB BC A
4cos cos 4sin
22 2
+−
=−=
22
ABC
4sin cos 1 0
22
−

=−≤


VËy (1) ®óng víi mäi x.
2) sin x cosx 10
cosx sin x sin x cosx 3
+
++ =
§Æt tcosxsinx( 2t 2)=+−≤≤
(2)
th× 2
t12sinxcosx=+ vµ ta ®−îc +=
−
2
2t 10
t3
t1
§Æt ®iÒu kiÖn t ≠ ±1 sÏ tíi
32
3t 10t 3t 10 0
−++=
tøc lµ : 1 + a + b + c + ab + ac + bc ≥ 0 (2)
Céng (1) vµ (2) ta cã : abc + 2 (1 + a + b + c + ac + bc + ac) ≥ 0.
hay 2
(t 2)(3t 4t 5) 0−−−=
.
Ph−¬ng tr×nh nµy cã ba nghiÖm
1
t2
= ; 2
219
t3
−
= ; 3
219
t3
+
=
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
_________________________________________________________
ChØ cã 2
t lµ thÝch hîp. Thay vµo (2) ta cã ph−¬ng tr×nh
219
cos x 432
π−

−=

 .
§Æt 219
cos 32
−
α= th× ®−îc hai hä nghiÖm :
1
x2k
4
π
=+α+π ; 2
x2m
4
π
=−α+ π
C©u III.
1) §Æt ®iÒu kiÖn x - a ≠ 0 ; x + a ≠ 0 th× (1) ®−îc biÕn ®æi vÒ d¹ng :
2
x[a 1)x a a 2b] 0−+++ =
(2)
Víi ∀a, b (2) ®Òu cã nghiÖm 1
x0=.
Gi¶i 2
(a 1)x a a 2b 0−+++=
.
NÕu a ≠ 1 cã nghiÖm
2
2
aa2b
x1a
++
=−
NÕu a = 1 ta cã : 0x = − 2(1 + b). (3)
Víi b ≠ − 1 th× (3) v« nghiÖm ; víi b = -1 th× (3) nghiÖm ®óng víi ∀x. KiÓm tra 2
x cã tháa
m·n ®iÒu kiÖn 2
xa≠± ?
22
2
aa2b
xa aaa2b
1a
++
≠⇔ ≠⇔ ++ ≠
−
≠ 22 2
aa 2(a b)0 b a−⇔ +≠⇔≠−
222
2
aa2b
xa aaa2baaba
1a
++
≠− ⇔ ≠− ⇔ + + ≠ − ⇔ ≠−
−.
KÕt luËn :
víi b ≠ −1 , (1) cã nghiÖm duy nhÊt 1
x0=.
víi b = − 1, (1) cã nghiÖm lµ ∀x ≠ ± 1.
NÕu a ≠ 1 ; 0 th× :
víi 2
b
a≠− , b ≠ - a, (1) cã hai nghiÖm
=
1
x0,
++
=−
2
2
aa2b
x1a
víi 2
b
a=− hoÆc b = - a th× (1) cã mét nghiÖm 1
x0=.
NÕu a = 0 th× (1) cã mét nghiÖm 2
x2b= nÕu b ≠ 0 ; (1) sÏ v« nghiÖm nÕu b = 0.
2) V× 222
abc1++=
nªn - 1 ≤ a, b, c ≤ 1.
Do ®ã 1 + a ≥ 0 , 1 + b ≥ 0, 1 + c ≥ 0 ⇒ (1 + a) (1 + b) (1 + c) ≥ 0 ⇒
⇒ 1 + a + b + c + ab + ac + bc + abc ≥ 0. (1)
MÆt kh¸c :
2
222 (1 a b c)
a b c a b c ab ac bc 0
2
+++
++++++++= ≥
,
NÕu a = 1 th× :
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________
C©u IVa. 1) Víi x >0tacã
F(x)=x-ln(1 + x) ÞF’(x) = 1- 1
1+ x =x
1+ x
;
víix<0tacã
F(x)=-x-ln(1 - x) ÞF’(x) = -1 + 1
1- x =x
1- x
.
Tõ ®ã suy ra víi x ¹0
F’(x) = x
1+|x|
.
Ta chØ cßn ph¶i chøng minh r»ng F’(0) = 0. Qu¶ vËy
F’(0) = lim 1
x(F( x) - F(0))
x0∆∆∆
→=()
lim 1
xx-ln(1+ x) =
x0∆∆∆∆
→
=lim 1 - ln(1 + x)
x=
x0∆
∆
∆
→
0,
v× lim ln(1 + x)
x=1
x0∆
∆
∆
→.
2)I=
1
e
∫xln2xdx.
§æt ux
dv xdx
=
=
ln 2
⇒
du x
x
dx
vx
=
=
2
1
2
2
ln
,
suy ra I = 1
2x ln x - xlnxdx = e
2-J
22
1
e
1
e2
∫
, víi J =
1
e
xlnxdx
∫.
§Ó tÝnh J, ®Æt
ux
dv xdx
du ux
x
v
=
=
⇒=
=
ln
1
2
suy ra J = 1
2
1
22
1
41
2
1
2
2
1
xx xdx
e
e
ee
ln ()
−=−
−
∫.
VËy
I=1
4(e2- 1).
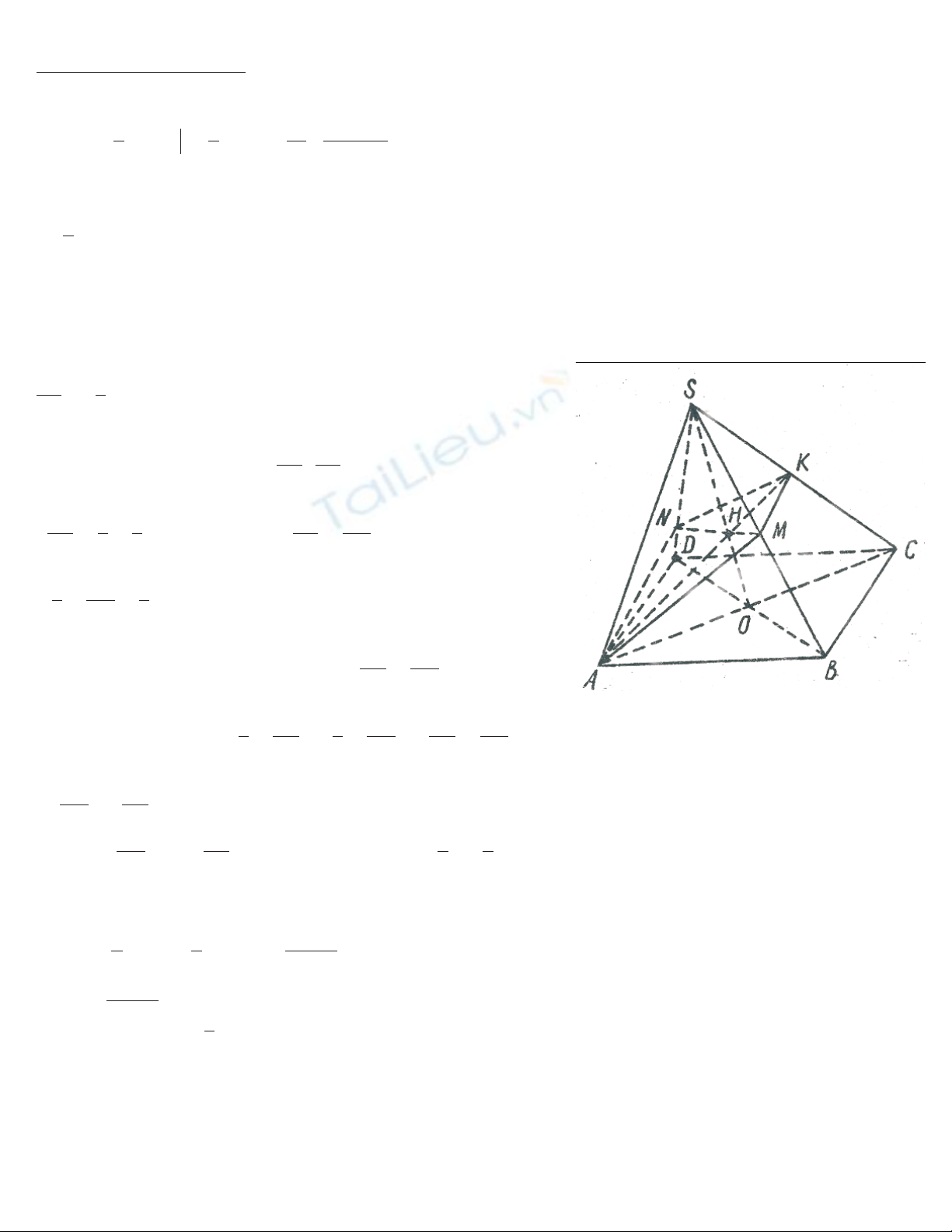
C©u Ivb.
1) V× K lµ trung®iÓm cña SC, nªn theo h×nhbªn, trong tam gi¸c SAC, SO
vµ AK lµ hai ®ûêng trungtuyÕn c¾t nhau t¹i trängt©m H, vËy
SH
SO =2
3.
Theo h×nh bªn , ta cã dt(SNH) =SN
SD .SH
SO . dt(SDO) =
=SN
SD .2
3.1
2dt(SDB),dt(SHM) =SH
SO .SM
SB .dt(SOB)
=2
3.SM
SB .1
2dt (SDB).
§ång thêi dt(SNH) + dt(SHM) = dt(SNM) = SN
SD .SM
SB dt(SDB).
Tõ c¸c hÖ thøc trªn, suy ra 1
3.SN
SD +1
3.SM
SB =SN
SD .SM
SD
ÛSB
SM +SD
SN =3
.
2) §Æt SM
SB =x,SN
SD =y,theo hÖ thøc trªn ta cã 1
x+1
y=3
. §ång thêi, do ý nghÜa h×nh häc, ph¶i cã0<x£1,
0<y£1. V×
1
y=3-1
xy= x
3x - 1
⇒,
nªn 0 <x
3x - 1 1≤
0<x£1
Þ1
2x1≤≤
.
www.khoabang.com.vn LuyÖn thi trªn m¹ng – Phiªn b¶n 1.0
________________________________________________________________________________