S GIÁO D C VÀ ĐÀO T O Ở Ụ Ạ
Đ NG THÁPỒ
TR NG THPT Đ C BINH KI UƯỜ Ố Ề
Đ ÔN T P KI M TRA CH T L NG H C KỲ IIỀ Ậ Ể Ấ ƯỢ Ọ
NĂM H C: 2012 – 2013Ọ
MÔN THI: TOÁN – L P 10Ớ
Th i gian : 90 phút ờ(không k th i gian phát đ )ể ờ ề
I. Ph n chung cho t t c các h c sinhầ ấ ả ọ (8,0 đi m)ể
câu 1.(3đi m) ể
1. gi i ph ng trình, b t ph ng trình sauả ươ ấ ươ
a)
2 5 4x x− = −
b)
( )
2
( 3) 2 0x x x+ − − + <
2. gi i b t ph ng trình: ả ấ ươ
2 2 1x x+ + −
câu 2.(3đi m)ể
a) tính các giá tr l ng giác còn l i c a góc ị ượ ạ ủ
α
bi t ế
3
sin 5
α
=
và
2
πα π
< <
b) v i ớ
sin 0x
. rút g n bi u th c sau: ọ ể ứ
2
2
2
1 cos
A = 2cot x
1 cos
x
x
+−
−
câu 3.(2đi m) ể
trong m t ph ng oxy, cho hai đi m m(-1;0) và n(5;-2)ặ ẳ ể
a) vi t ph ng trình tham s c a đ ng th ng ế ươ ố ủ ườ ẳ
bi t đi qua hai đi m m và nế ể
b) vi t ph ng trình đ ng tròn (c) có đ ng kính làmnế ươ ườ ườ
II. Ph n t ch n (2,0 đi m) ầ ự ọ ể (h c sinh ch n 1 trong 2 ph n)ọ ọ ầ
1.Theo ch ng trình chu nươ ẩ
câu 4a.(2,0đi m)ể
a) tìm m đ ph ng trình sau cĩ 2 nghi m tri d u: ể ươ ệ ấ
m x m x m
2
(2 1) 3( 1) 1 0− + + + + =
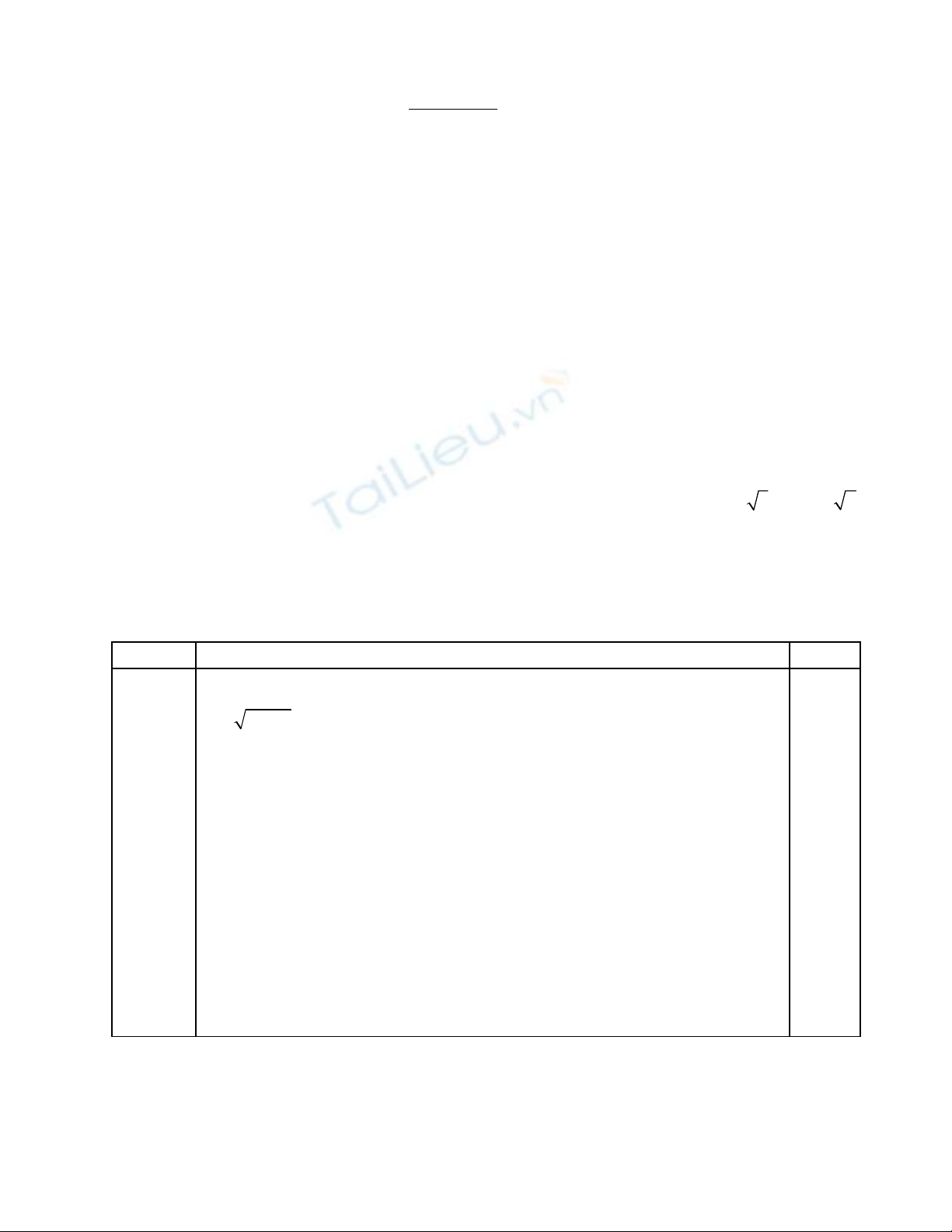
b) gi i b t ph ng trình sau: ả ấ ươ
2
2 3 2 2
1
x x x
x
− − − >
−
câu 5a.(1đi m)trong tam giác abc v i ể ớ
2
.AC AB BC=
.
ch ng minh r ng: ứ ằ
2
sin sin .A B sinC
=
2. Theo ch ng trình nâng caoươ
câu 4b.(2,0đi m)ể
a) tìm m đ b t ph ng trình: (m + 1)xể ấ ươ 2 − 2(m − 1)x + 3m − 3 < 0 vô nghi m v i m i x ệ ớ ọ
2) trong tam giác abc v i ớ
2
.AC AB BC=
.
ch ng minh r ng: ứ ằ
2
sin sin .A B sinC
=
câu 5b.(1,0đi m)ể
vi t ph ng trình chính chính t c c a elip (e) bi t đi qua 2 đi m ế ươ ắ ủ ế ể
(4, 3)M−
và
(2 2,3)N
---h t---ế
đáp án
câu n i dungộđi mể
câu1
(3đ)
a) gi i ph ng trìnhả ươ
2 5 4x x− = −
2
2
4 0
2 5 ( 4)
4
10 21 0
x
x x
x
x x
−
− = −
− + =
4
7( )
3( )
x
x n
x l
=
=
7x
=�
v y x = 7 ậ
0.25
0.25
0.5
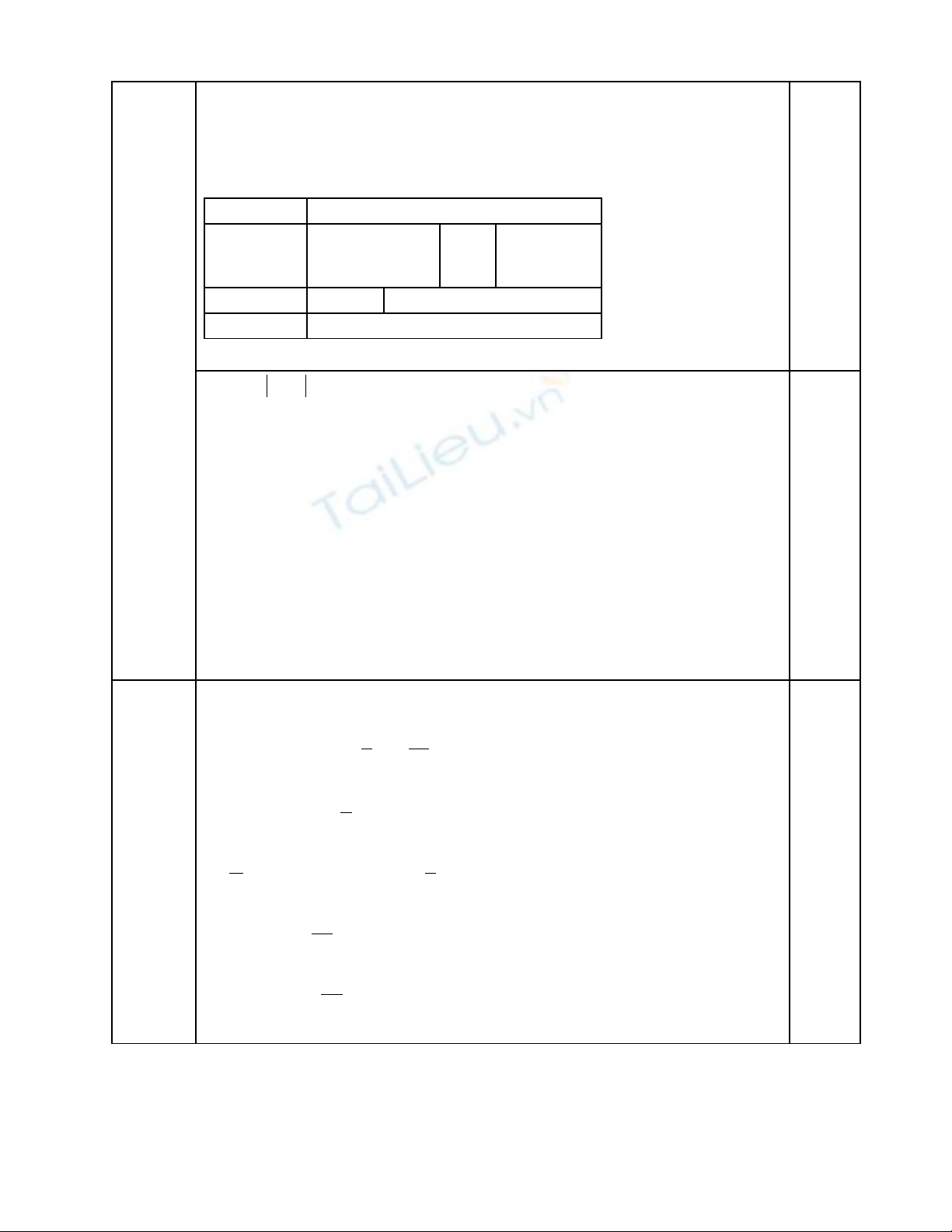
b)ta có:
x 3 0 3x+ = = −�
2
2 0 1; 2x x x x− − + = = = −�
b ng xét d u:ả ấ
x
−
-3 -2 1
+
x 3
+
- 0
+
+ +
2
2x x− − +
- - 0 + 0 -
vt + 0 - 0 + 0 -
v y s = (-3;-2) ậ∪ (1;
+
)
0.25
0.25
0.25
0.25
b)
2 2 1x x+ + −
(*)
n u ế
2 0 2x x+ −�۳
(*)
2 2 1 1x x x
+ + − −� ۳
giao v i đi u ki n ớ ề ệ
[
)
1
1;S= − +
n u ế
2 0 2x x
+ < < −�
(*)
2 2 1 1x x x−− −� ۳
giao v i đi u ki n ớ ề ệ
2
S=
v y s = ậ
[
)
1 2
1;S S S= = − +� �
0.25
0.25
0.25
0.25
câu2.
(3đ)
a) ta có
2 2
cos 1 sin
α α
= −
2
3 16
15 25
� �
= − =
� �
� �
4
cos 5
α
=� �
vì
2
πα π
< <
nên
4
cos 5
α
= −
ta có
3
tan 4
α
−
=
4
t3
co
α
−
=
0.5
0.5
0.5
0.5
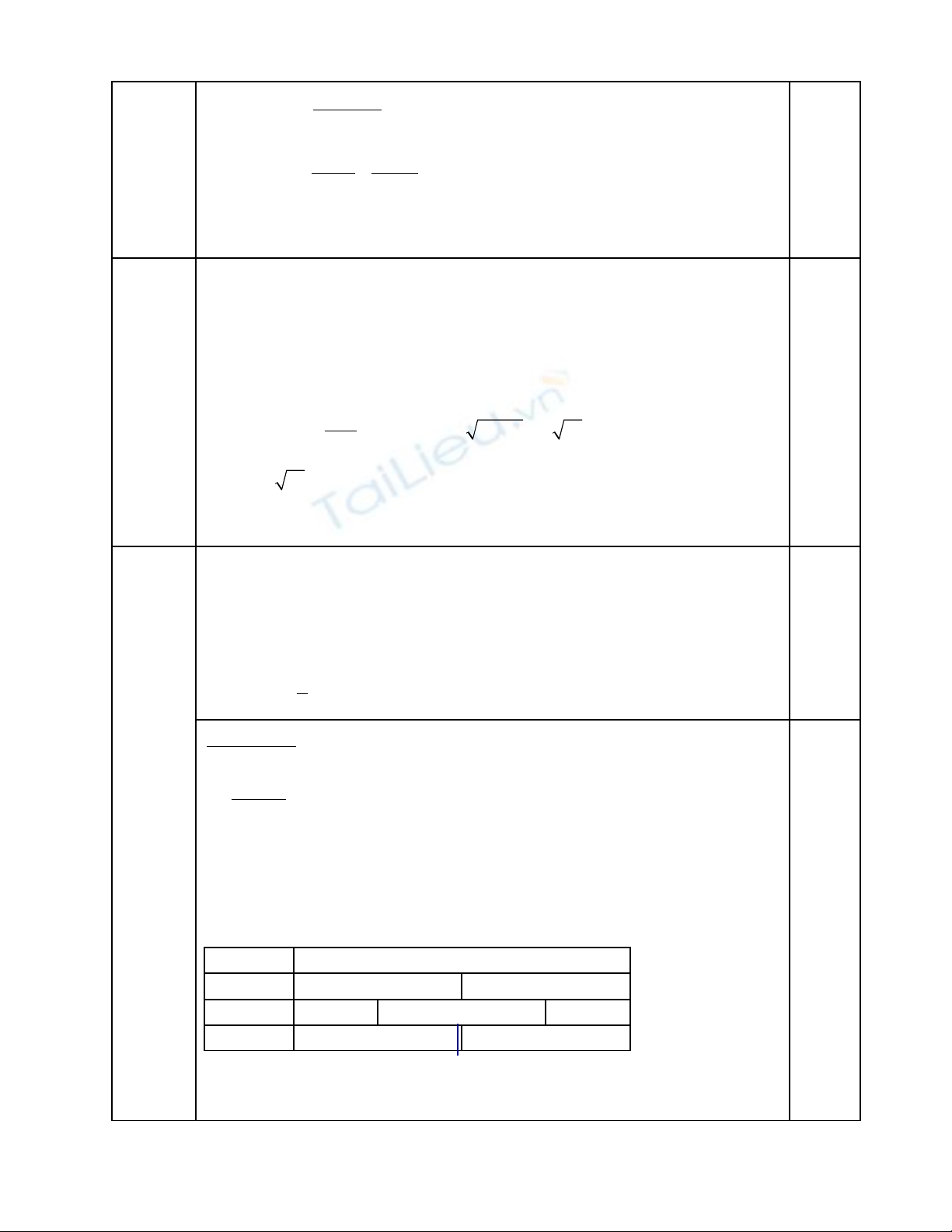
b)ta có
2
2
2
1 cos
A = 2cot x
1 cos
x
x
+−
−
2
2
2 2
1 cos
= 2cot x
sin sin
x
x x
+ −
2 2 2
= 1+cot x cot x - 2cot x = 1+
0.5
0.5
câu3
2đ
a)véct ch ph ng ơ ỉ ươ
(6; 2)u MN= = −
r uuuur
và đi m m(-1;0) ể
1 6
:2
x t
dy t
= − +
= −
b) tâm i là trung đi m c a mn nên i(2;-1)ể ủ
bán kính
2
MN
R=
mà
36 4 2 10MN = + =
nên
10R=
v y (c): ậ
( )
22
x 2 ( 1) 10y− + + =
0.5
0.5
0.25
0.25
0.5
câu4a
2,0đ
1)
m x m x m
2
(2 1) 3( 1) 1 0− + + + + =
cĩ 2 nghi m tri d u ệ ấ ⇔ ac < 0
(2 1)( 1) 0− + <�m m
1
1; 2
� �
−� �
� �
� �
m
0,25
0,25
0,5
2
2
2 3 2 2
1
40
1
x x x
x
x x
x
− − − >
−
−>�−
cho
2
4 0 0; 4x x x x− = = =�
1 0 1x x
− = =�
b ng xét d uả ấ
x
−
0 1 4
2
4x x−
+ 0 - - 0 +
x – 1 - - 0 + +
vt - 0 + - 0 +
v y s = (0;1) ậ∪ (4;
+
)
0.25
0.5
0.25
câu5a
1,0đ ta có
sin sin sin
BC AC AB
A B C
= =
.sin (1)
sin
.sin (2)
sin
BC B
AC A
BC C
AB A
=
=
th (1) và (2) vàoế
2
.AC AB BC=
ta đ c ượ
.sin
sin
BC B
A
.
2
.sin
sin
BC C BC
A=
2
sin sin .A B sinC
=
0.5
0.25
0.25
câu4b
2,0đ
a)ta th y ấ
2
6 12 7 0;x x x− + > ∀ ﾡ
ph ng trình ươ
2 2
6 12 7 6 6 12 7 7 0x x x x− + − − + − =�
đ t t = ặ
2
6 12 7x x− +
;
0t
ph ng trình tr thành: ươ ở
2
6 7 0t t− − =
1
7
t
t
= −
=
k t h p đi u ki n t > 0 ta đ c t = 7 ế ợ ề ệ ượ
nên
2
2
6 12 7 49
2 7 0
1 2 2
x x
x x
x
− + =
− − =�
=� �
v y ph ng trình có hai nghi m: ậ ươ ệ
1 2 2x=
0.25
0.25
0.25
0.25
b)đ t f(x)=(m + 1)xặ2 − 2(m − 1)x + 3m − 3 < 0 vô nghi m v iệ ớ
m i x khi và ch khi :ọ ỉ
( ) 0f x
;
x
∀
ﾡ
hay f(x)=(m + 1)x2 − 2(m − 1)x + 3m − 3
0
;
x
∀
ﾡ
nh n th y m = -1 không th a ậ ấ ỏ
do đó
( ) 0f x
;
x
∀
ﾡ
2
1 0
2 2 4 0
1
( ; 2) (1; )
m
m m
m
m
+ >
− − +
> −
− − +� � � �
0.25
0.25