ĐỀ THI CHỌN HỌC SINH GIỎI THỊ XẤ HÀ ĐÔNG, HÀ
TÂY
Môn Toán lớp 7 (2003 - 2004)
(Thời gian : 120 phút)
o Bài 1 : (4 điểm) Cho các đa thức :
f(x) = 2x5 - 4x3 + x2 - 2x + 2
g(x) = x5 - 2x4 + x2 - 5x + 3
h(x) = x4 + 4x3 + 3x2 - 8x +
a) Tính M(x) = f(x) - 2g(x) + h(x).
b) Tính giá trị của M(x) khi :
c) Có giá trị nào của x để M(x) = 0 ?
o Bài 2 : (4 điểm)
a) Tìm 3 số a, b, c biết : 3a = 2b ; 5b = 7c và 3a + 5c - 7b = 60.
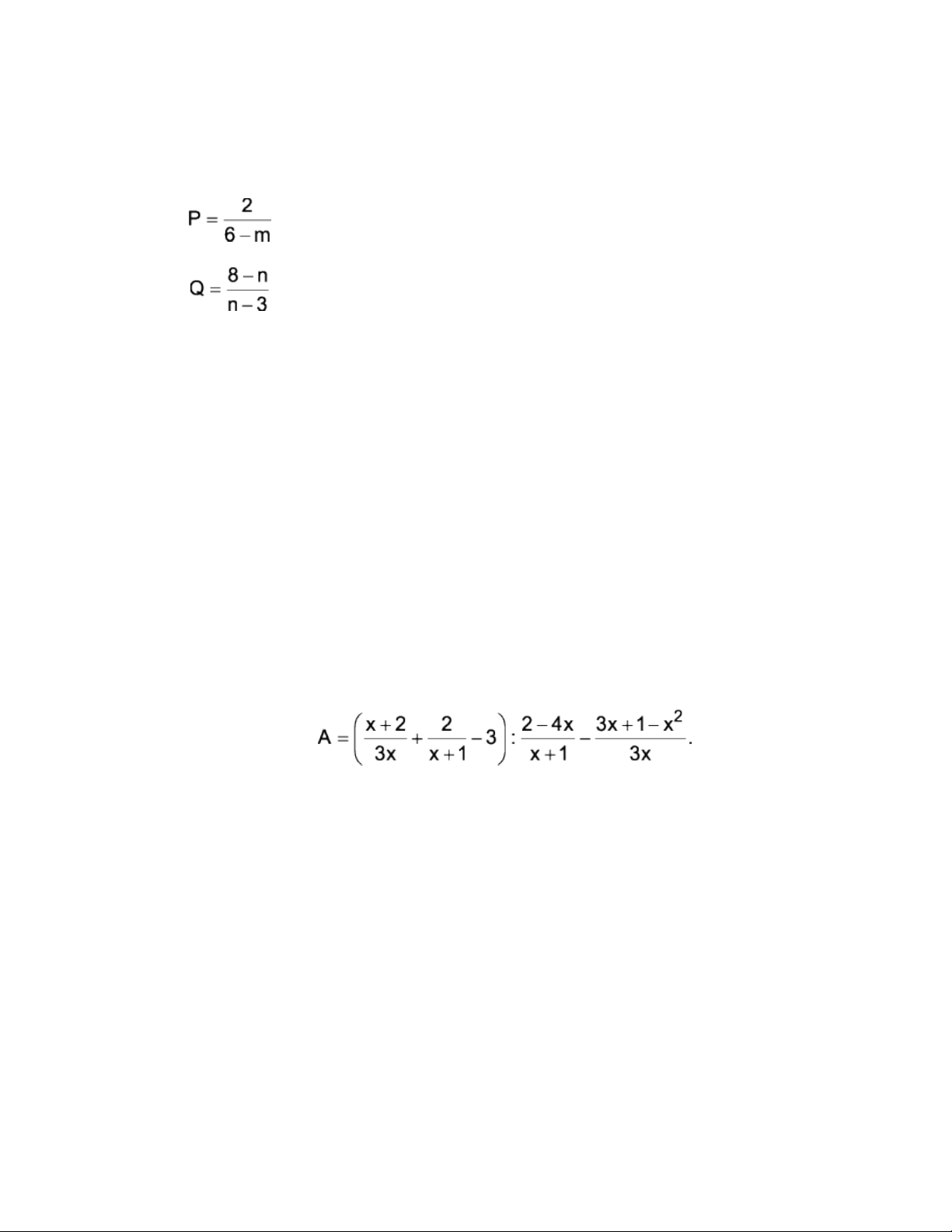
b) Tìm x biết : |2x - 3| - x = |2 - x|.
o Bài 3 : (4 điểm) Tìm giá trị nguyên của m, n để biểu thức :
a) có giá trị lớn nhất.
b) có giá trị nguyên nhỏ nhất.
o Bài 4 : (5 điểm) Cho tam giác ABC có AB < AC, AB = c, AC = b. Qua M là trung
điểm của BC ngƣời ta kẻ đƣờng vuông góc vớ iđƣờng phân giác trong của A đƣờng
thẳng này cắt các đƣờng thẳng AB, AC lần lƣợt tại D và E.
a) Chứng minh : BD = CE.
b) Tính AD và BD theo b, c.
o Bài 5 : (3 điểm) Cho tam giác ABC cân tại A, A = 100o, D là một điểm thuộc miền
trong của tam giác ABC sao cho DBC = 10o, DCB =20o. Tính ADB.
Môn Toán lớp 8 (2003 - 2004)
(Thời gian : 150 phút)
o Bài 1 : (5 điểm) Cho
a) Rút gọn A.
b) Tìm A để x = 6013.
c) Tìm x để A < 0.
d) Tìm x để A nguyên
o Bài 2 : (3 điểm)
Cho A = (x + y + z)3 - x3 - y3 - z3
a) Rút gọn A.
b) Chứng minh A chia hết cho 6 với mọi x, y, z nguyên.
o Bài 3 : (4 điểm)
Sau một loạt bắn đạn thật của 3 chiến sĩ Hùng, Dũng, Cƣờng (mỗi ngƣời bắn một viên),
ngƣời báo bia cho biết có ba điểm khác nhau là 8, 9, 10 và thông báo :
a) Hùng đạt điểm 10.
b) Dũng không đạt điểm 10.
c) Cƣờng không đạt điểm 9.
Đồng thời cho biết trong 3 thông báo trên chỉ có một thông báo là đúng, hãy cho biết kết
quả điểm bắn của mỗi ngƣời.
o Bài 4 : (5 điểm)
Cho tam giác ABC vuông tại A, AB = c, AC = b. Lần lƣợt dựng trên AB, AC, bên ngoài
tam giác ABC các tam giác vuông cân ABD tại D, ACE tại E.
a) Chứng minh các điểm E, A, D thẳng hàng.
b) Gọi trung điểm của BC là I, chứng minh tam giác DIE vuông.
c) Tính diện tích tứ giác BDEC.
d) Đƣờng thẳng ED cắt đƣờng thẳng CB tại K. Tính các tỉ số sau theo b và c
o Bài 5 : (3 điểm)
Cho tứ giác ABCD, M là một điểm trên CD (khác C, D).
Chứng minh rằng MA + MB < max {CA + CB ; DA + DB} (kí hiệu max {CA + CB ;
DA + DB} là giá trị lớn nhất trong 2 giá trị CA + CB ; DA + DB).
ĐỀ THI HỌC SINH GIỎI QUẬNN HOÀN KIẾM, HÀ NỘI
2003 - 2004
Môn toán lớp 7
(Thời gian : 120 phút)
Bài 1 : (4 điểm)
Giải phƣơng trình