Đ THI CH N H C SINH GI IỀ Ọ Ọ Ỏ
GI I TOÁN TRÊN MÁY TÍNH CASIOẢ
NĂM H C 2009 – 2010 -L p 12 THPTỌ ớ
Đi m c a toàn bài thiể ủ Các giám kh oả
(H , tên và ch ký)ọ ữ S pháchố
(Do Ch t ch H i đ ng ch m thi ghi)ủ ị ộ ồ ấ
B ng sằ ố B ng chằ ữ
Giám kh o 1:ả
Giám kh o 2:ả
Qui đ nh:ị H c sinh trình bày v n t t cách gi i, công th c áp d ng, k t qu tính toán vào ôọ ắ ắ ả ứ ụ ế ả
tr ng li n k bài toán. Các k t qu tính g n đúng, n u không có ch đ nh c th , đ c ng m đ nhố ề ề ế ả ầ ế ỉ ị ụ ể ượ ầ ị
chính xác t i 4 ch s ph n th p phân sau d u ph y.ớ ữ ố ầ ậ ấ ẩ
Bài 1 : Cho hàm s ố
2
2
2 5 3
( ) 3 1
x x
y f x x x
− +
= = − −
Tính kho ng cách gi a hai đi m c c tr c a đ th hàm s đã choả ữ ể ự ị ủ ồ ị ố .
Cách gi iảK t quế ả
AB ≈
Bài 2 : Tính g n đúng hoành đ giao đi m c a hai đ th hàm s : ầ ộ ể ủ ồ ị ố
3 2
1
( ) : ( ) 2 3 1C y f x x x x= = − − −
và
2 33 3
2
( ) : ( ) 2 2 3 1= = + − − +C y g x x x x
.
Cách gi iảK t quế ả
1
x≈
2
x
≈
3
≈
x
Bài 3 Cho hai dãy s ố
( )
n
u
và
( )
n
v
có :
1 1 1 1
1; 2; 22 15 ; 17 12 ,( 1)
n n n n n n
u v u v u v v u n
+ +
= = = − = − ≥
.
a/ Tính
b/ L p quy trình n phímậ ấ .
Cách gi iảK t quế ả
Quy trình n phím : ấ
Bài 4 Tìm s t nhiên th 2010 sau d u ph y khi chia 1 cho 23ố ự ứ ấ ẩ
Cách gi iảK t quế ả
Bài 5 : Cho hàm s ố
3 2
( ) 2 3( 3) 18 8y f x x a x ax= = − + + −
. Tìm a đ đ th hàm s ti p xúc v i tr cể ồ ị ố ế ớ ụ
hoành.
Cách gi iảK t quế ả
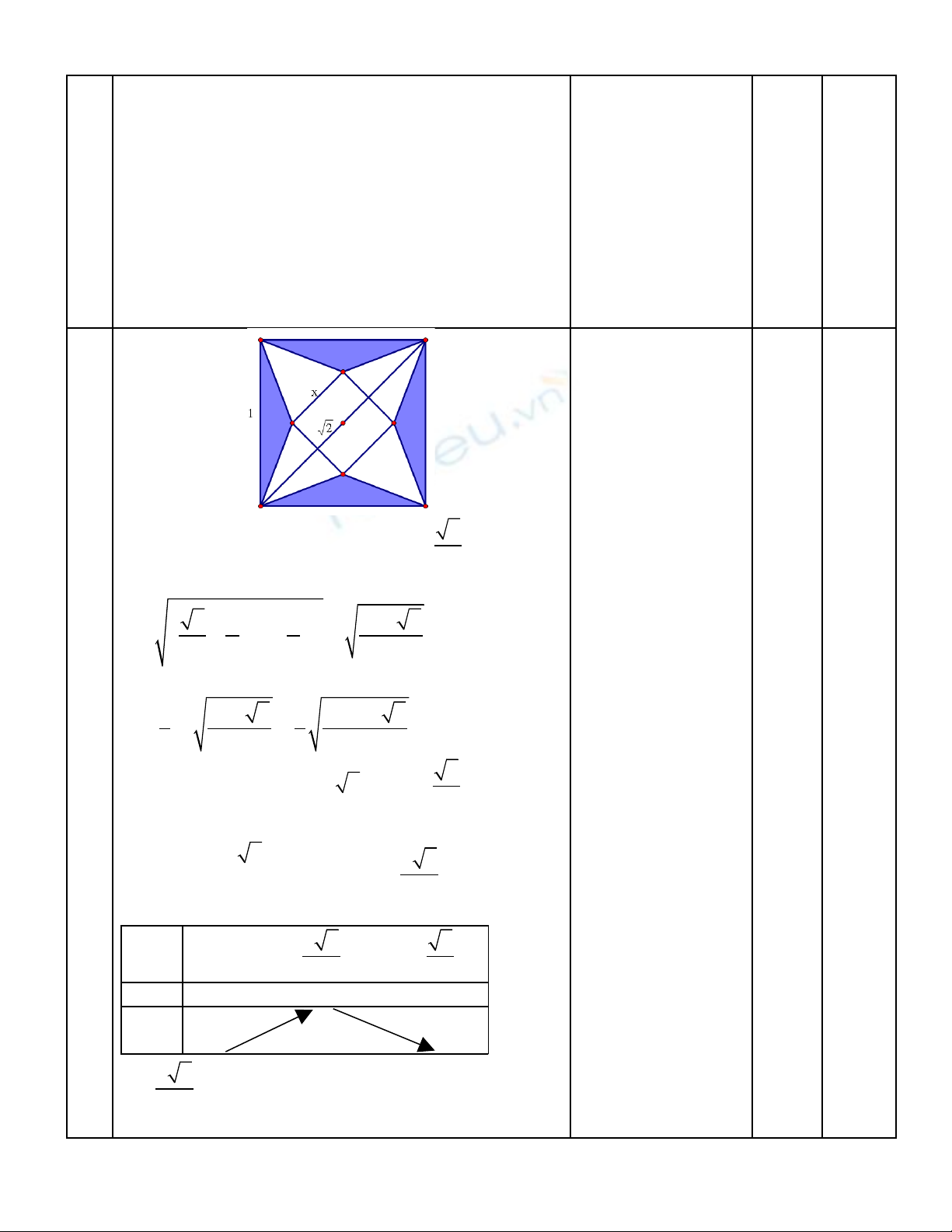
Bài 6 : Ng i ta c t m t t gi y hìnhvuông c nh b ng 1 đ g p thành m t hình chóp t giác đ uườ ắ ộ ờ ấ ạ ằ ể ấ ộ ứ ề
sao cho b n đ nh c a hình vuông dán l i thành đ nh c a hình chóp .Tính c nh đáy c a kh i chóp đố ỉ ủ ạ ỉ ủ ạ ủ ố ể
th tích l n nh t.ể ớ ấ
Cách gi iảK t quế ả
Bài 7 : M t ng i đ c lĩnh l ng kh i đi m là 700.000đ/tháng. C ba năm anh ta l i đ c tăngộ ườ ượ ươ ở ể ứ ạ ượ
l ng thêm 7%. H i sau 36 năm làm vi c anh ta đ c lĩnh t t c bao nhiêu ti n (L y chính xác đ nươ ỏ ệ ượ ấ ả ề ấ ế
hàng đ n v ). ơ ị
Cách gi iảK t quế ả
CÁCH GI I, ĐÁP S VÀ H NG D N CHO ĐI MẢ Ố ƯỚ Ẫ Ể
Bài Cách gi iảĐáp sốĐi mể
t ngừ
ph nầ
Đi mể
toàn
bài
1
*
2
2
13x 22x 8
y' 3x x 1
− +
=− −
;
11 17
y' 0 x 13
±
= ⇔ =
*
11 17 11 17
ShiftSTOA, ShiftSTOB
13 13
+ −
*
f (A)ShiftSTOC, f (B)ShiftSTOD
2 2
*AB (ALPHA A ALPHA B) (ALPHAC ALPHA D)= − + −
AB 1,4184≈
0,75x
21,5
2
* Hoành đ giao đi m c a hai đ th là nghi m c aộ ể ủ ồ ị ệ ủ
ph ng trình :ươ
3 2 2 33 3
2 3 1 2 2 3 1− − − = + − − +x x x x x x
* 2ALPHA X SHIFT x3– ALPHA X x2 – 3ALPHA X
– 1 ALPHA = SHIFT
3
ALHA X x2 + 2
〉
– SHIFT
3
ALHA X SHIFT x3 – 3 ALPHA X +1
1
x 1,6180≈
1
x 0,6180≈ −
1
x 0,5≈ −
0.25
1.25 1.5
3
* 1 SHIFT STO A 2 SHIFT STO B 1 SHIFT STO X
ALPHA X ALPHA = ALPHA X + 1 ALPHA :
ALPHA C ALPHA = 22 ALPHA B – 15 ALPHA A
ALPHA : ALPHA D ALPHA = 17 ALPHA B -12
ALPHA A ALPHA : ALPHA X ALPHA = ALPHA X
+ 1 ALPHA : ALPHA A ALPHA = 22 ALPHA D – 15
ALPHA C ALPHA : ALPHA B ALPHA = 17 ALPHA
D -12 ALPHA C CALC = = =…… đ n khi X = X + 1ế
b ng m t trong các giá tr 5; 10; 15; 18 thì n thêm : =ằ ộ ị ấ
= = r i ghi k t quồ ế ả
5
10
15
18
5
10
5
5
u 767
u 192547
u 47517071
u 1055662493
v 526
v 135434
v 34219414
v 673575382
= −
= −
= −
=
= −
= −
= −
=
0,5
0,25x
41.5
4
*
10,(0434782608695652173913)
23 =
* 2010 ≡ 8 (mod 22)
* s c n tìm là 8ố ầ
S th p phân thố ậ ứ
2010 sau d u ph yấ ẩ
là 8
0,5x2 1.0
5
* ĐTHS ti p xúc Ox k.v.c.k hpt sau có nghi m : ế ệ
3 2
2
2x 3(a 3)x 18ax 8 0
6x 6(a 3)x 18a 0
− + + − =
− + + =
3 2
2x 3(a 3)x 18ax 8 0
x 3
x a
− + + − =
⇔=
=
3 2
27a 35 0
a 9a 8 0
− =
⇔− + − =
a 1
a 1,2963
a 8,8990
a 0,8990
=
≈
≈
≈ −
0,5
0,5x2
1.5
6
* G i c nh đáy hình chóp là x, ọ ạ
2
x (0; )
2
∈
.
Chi u cao c a hình chóp là :ề ủ
22
2 x x 1 x 2
h2 2 2 2
−
= − − =
Th tích c a kh i chóp :ể ủ ố
4 5
2
1 1 x 2 1 x x 2
V x
3 2 3 2
− −
= =
* Xét hàm s : ố
4 5
y x x 2= −
trên
2
(0; )
2
3 4
x 0 (l)
y' 4x 5x 2 ; y' 0 2 2
x (n)
5
=
= − = ⇔ =
BBT :
x 0
2 2
5
2
2
y’ ║ + 0 - ║
y ║ ║
║ ║ V y khiậ
2 2
x5
=
thì kh i chóp đ t GTLNố ạ
C nh đáy kh iạ ố
chóp là :
x 0,5657≈
.
0,75x
2
1.5