ĐỀ THI HỌC KÌ I
MÔN: TOÁN 12
Thời gian: 90 phút ( Không kể thời gian giao đề )
Họ và tên: ……………………………………Lớp:……………SBD:……
Bài 1: (4 điểm)
Cho hàm số 3 2 2
1
1 1
3
= = - + - + +
y f(x) x mx (m m )x có đồ thị là (Cm)
a. Khảo sát và vẽ đồ thị (C) khi m = 2.
b. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là
nghiệm của phương trình y// = 0.
c. Xác định m để hàm f cực đại tại x = 1.
Bài 2: (3 điểm)
a. Giải phương trình:
- + =
x x
.
16 17 4 16 0
.
b. Giải bất phương trình:
+ £ +
log (x ) log (x x)
2 2
1.
Bài 3: (3 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a,
SA
^
(ABCD) và SA = a.
a. Tính thể tích khối chóp S.ABCD.
b. Gọi I là trung điểm của SC. Chứng minh rằng: I là tâm mặt cầu ngoại tiếp
hình chóp S.ABCD. Tính bán kính mặt cầu đó.
c. Tính diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABCD.
……………..Hết……………..
ĐỀ THI HỌC KÌ I
MÔN: TOÁN 12
Thời gian: 90 phút ( Không kể thời gian giao đề )
Họ và tên: ……………………………………Lớp:……………SBD:……
Bài 1: (4 điểm)
Cho hàm số 3 2 2
1
1 1
3
= = - + - + +
y f(x) x mx (m m )x có đồ thị là (Cm)
a. Khảo sát và vẽ đồ thị (C) khi m = 2.
b. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ là
nghiệm của phương trình y// = 0.
c. Xác định m để hàm f cực đại tại x = 1.
Bài 2: (3 điểm)
a. Giải phương trình:
- + =
x x
.
16 17 4 16 0
.
b. Giải bất phương trình:
+ £ +
log (x ) log (x x)
2 2
1.
Bài 3: (3 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a,
SA
^
(ABCD) và SA = a.
a. Tính thể tích khối chóp S.ABCD.
b. Gọi I là trung điểm của SC. Chứng minh rằng: I là tâm mặt cầu ngoại tiếp
hình chóp S.ABCD. Tính bán kính mặt cầu đó.
c. Tính diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABCD.
……………..Hết……………..
Đáp án: MÔN TOÁN LỚP 12.
ĐỀ KIỂM TRA HỌC KỲ I
------
Bài 1: 4 điểm
a. Khảo sát hàm số khi m = 2 2.đ
TXĐ: R
0.25đ
2
1
4 3 0
3
é
=
ê
= - + = Û ê
=
ë
/x
y x x x
0.50đ
BBT:
0.75đ
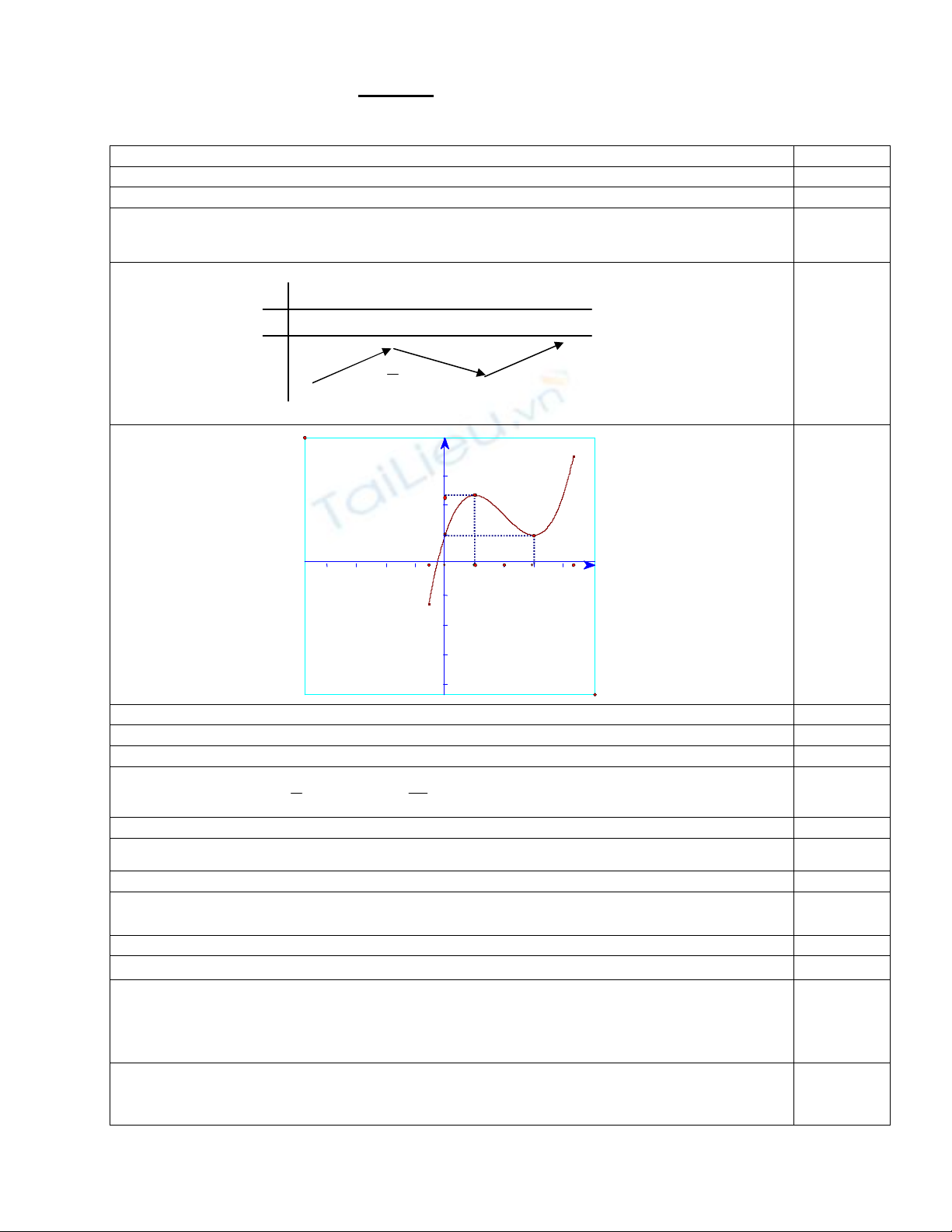
Đồ thị:
0.50đ
b. Vi
ết pttt của đồ thị (C) tại điểm có ho
ành đ
ộ l
à nghi
ệm của ph
ương tr
ình y
//
=0
1đ
Ta có: y
//
= 2x
–
↔ x = 2, y
/
(2) =
–
1
0.50đ
Tiếp điểm A(2; 4) 0.25đ
PTTT: = - - + Û = - +y (x ) y x
5 11
2
3 3
0.25đ
c. Tìm m để hàm f đạt cực đại tại x = 1. 1đ
= - + - +
/
y x mx m m
2 2
2 1
0.25đ
Hàm f đạt cực đại tại x = 1 nên y
/
(1) = 0 ↔ m
2
– m + 1 = 0 ↔ m = 1 v m = 2 0.25đ
m = 1: y
/
= ( x – 1 )
2
≥ 0, x
m = 2: theo câu a hàm f đ
ạt cực đại tại x = 1
0.50đ
Bài 2:
3 đi
ểm
a. Giải phương trình:
- + =
16 17.4 16 0
x x .
1.5 đ
Đặt: =
x
t
4
(t > 0)
Phương trình trở thành:
- + =
t .t
2
17 16 0
é=
ê
Ûê=
ë
t
t
1
16
0.75đ
é
é é
= = =
ê
ê ê
Û Þ Þ
ê
ê ê
= =
=
ê
ë ë
ë
x
x
t x
t x
2
1 4 1 0
16 2
4 4 0.75đ
x
y
/
y
– ∞ 1 3 + ∞
0 0 –
+ +
– ∞
+ ∞
3
7 1
x
y
3
7/3
O
1
1
b. Giải bất phương trình:
+ £ +
log (x ) log (x x)
2
2 2
1. 1.5đ
ì+ >
ï
ï
Ûí
ï
+ £ +
ï
î
x
pt
x x x
2
1 0
1
0.75đ
ì> - ì
ï> -
ï
ï ï
Û Û Û ³
í í
ï ï £ - Ú ³
- ³ ï
î
ï
î
xxx
x x
x2
11
1
1 1
1 0 0.75đ
Bài 3: 3 điểm
a. Tính thể tích khối chóp S.ABCD. 1 đ
Vì SA(ABCD) nên: =
S.ABCD ABCD
V S .SA
1
3
Mà: =
ABCD
S a
2
, SA = a
Suy ra: =
S.ABCD
a
V
3
3
0.5
0.25
0.25
b. Gọi I là trung điểm của SC. Chứng minh rằng I là tâm mặt cầu ngoại tiếp hình chóp
S.ABCD. Tính bán kính mặt cầu đó.
1.50 đ
Vì SA
(ABCD) nên
SAC vuông. Do đó: IS = IC = IA.
Chứng minh SBC vuông IS = IC = IB
Chứng minh SDC vuông IS = IC = ID
Vậy I cách đều 5 đỉnh của hình chóp nên I là tâm mặt cầu ngoại tiếp hình chóp.
* Bán kính: R = IS = SC/2
= + = + + = Þ =
SC SA AC SA AB BC a SC a
2 2 2 2 2 2 2
3 3
Vậy: =
a
R
3
2
0.25
0.25
0.25
0.25
0.50
c. Tính diện tích xung quanh mặt cầu ngoại tiếp hình chóp S.ABCD. 0.5 đ
p p p
= = =
a
S r ( ) a
2 2 2
3
4 4 3
2
0.50
Chú ý: Ở mỗi phần, mỗi câu nếu học sinh có cách giải khác đáp án nhưng đúng và chặt chẽ thì vẫn cho điểm
tối đa của phần hoặc câu đó.
A
D
B
C
S
I