PHÒNG GD ANH SƠN
TRƯỜNG THCS TÀO SƠN
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2013 - 2014
MÔN: TOÁN 7
( Thời gian 120 phút không kể thời gian giao đề)
Câu 1:(2 điểm)
a) Thực hiện phép tính:
2
112 51
::
223 32
⎛⎞
−
+
⎜⎟
⎝⎠
b) Xác đinh a để đồ thị hàm số y = ax đi qua điểm M(-2;-8). Vẽ đồ thị hàm số
vừa tìm được.
Câu 2:(2 điểm) Tìm x biết:
a.
()
14 2
3, 2
35 5
x−+=− +
b. Tìm
x
biết 21
2 .3 .5 10800
++ =
xxx
Câu 3: (2 điểm) a. Số A được chia thành 3 số tỉ lệ theo 231
::
546
. Biết rằng tổng các
bình phương của ba số đó bằng 24309. Tìm số A.
b. Cho ac
cb
=. Chứng minh rằng: 22
22
ac a
bc b
+
=
+( Với thiết các biểu thức đều
có nghĩa)
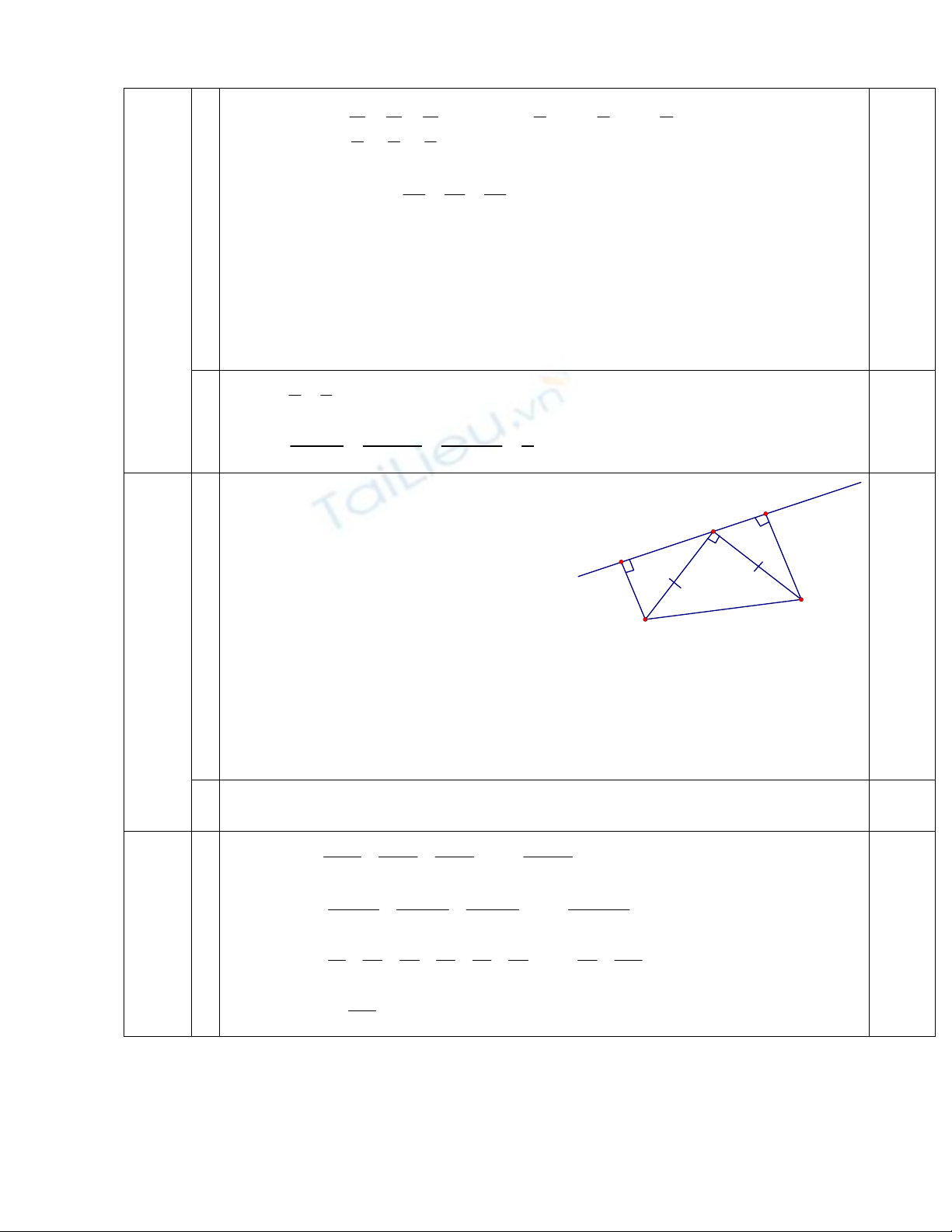
Câu 4: (3 điểm) Cho tam giác ABC có
0
A90=, AB = AC. Qua A vẽ đường thẳng d
sao cho B và C nằm cùng phía đối với đường thẳng d. Kẻ BH và CK vuông góc với d.
Chứng minh rằng:
a. AH = CK
b. HK = BH + CK
Câu 5: (1 điểm) Chứng minh rằng:
22 22 22 2 2
357 19
A1
1 .2 2 .3 3 .4 9 .10
=+++⋅⋅⋅+ <
----------------- Hết. -----------------
( Lưu ý: Cán bộ coi thi không giải thích gì thêm)
HƯỚNG DẪN CHẤM
Câu ý Đáp án Điểm
1
a
2
1 1 2 5 1 1 9 13 8 13 16 39 23
:: :
223 322166 96 18 18
−
−
⎛⎞
−+= − =− = =
⎜⎟
⎝⎠ 1,0
b
Vì đồ thị đi qua điểm M(-2;-8) nên ta có: - 8 = a.( -2) ⇒ a = 4
Vậy hàm số đã cho là; y = 4x.
Chọn A(1;4). Nối OA ta có đồ thị hàm số y = 4x.
0,5
0.5
2
a
()
12
3
12
3
17
x = 2 + =
33
1-5
x =-2 + =
33
14 2 14 162
3, 2
35 5 35 5 5
1414
35 5
12
3
−=
−=−
−
−+=− +⇔−+= +
⇔−+=
⎡
⎢
⇔−=⇔
⎢
⎢
⎣
⎡
⎢
⎢
⎢
⎣
⇔
x
x
xx
x
x
0.25
0.25
0.25
0.25
b
2
21
2 .3 .5 10800
2 .4.3 .3.5 10800
30 10800 :12 900
30 30
2
++ =
⇔=
⇔= =
⇔=
⇒=
xxx
x
x
xxx
x
0,25
0,25
0,25
0,25
3
a
Gọi a, b, c là ba số được chia ra từ số A.
Theo đề bài ta có: a : b : c = 231
::
546
(1)
và a2 +b2 +c2 = 24309 (2)
0,25
4
2
-2
-4
-5 5
Từ (1) ⇒231
546
abc
=== k ⇒23
;;
546
k
akbkc
=
==
Do đó (2) ⇔2491
( ) 24309
25 16 36
k++ =
⇒k = 180 và k = 180
−
+ Với k =180, ta được: a = 72; b = 135; c = 30.
Khi đó ta có A = a + b + c = 237.
+ Với k = 180−, ta được: a = 72
−
; b = 135
−
; c = 30−
Khi đó ta có A = 72
−
+( 135
−
) + ( 30
−
) = 237
−
.
0,25
0,25
0,25
b
Từ ac
cb
= suy ra 2.cab=
Ki đó 22 2
22 2
.()
.()
++ +
===
++ +
ac aabaab a
bc babbba b
0.5
0,5
4
a
Xét AHKΔ và CKHΔ có:
0
90HK==
AB = AC ( gt)
H
AB KCA= ( Cùng phụ với
K
AC )
⇒AHK = CKAΔΔ( g.c.g)
Suy ra: AH = CK ( Cặp cạnh tương ứng)
1,0
b Từ câu a AHK = CKAΔΔ suy ra: BH = AK ( Cặp cạnh tương ứng)
Vậy KH = AH + AK = BH + CK
0,5
0,5
5
Ta có:
22 22 22 2 2
22 22 22 22
22 22 22 2 2
222222 2 2
2
357 19
A
1 .2 2 .3 3 .4 9 .10
21 32 43 109
=
1 .2 2 .3 3 .4 9 .10
111111 1 1
=
122334 910
1
= 1- 1
10
=+++⋅⋅⋅+ =
−− − −
+++⋅⋅⋅+
−+−+−+⋅⋅⋅+−
<
0,5
0,5
( Lưu ý: Học sinh có cách giải khác mà đúng thì vẫn cho điểm tối đa)
A
B
C
H
K