PHÒNG GD&ĐT TP BẮC GIANG
TRƯỜNG THCS SONG MAI
ĐỀ KHẢO SÁT HỌC SINH GIỎI
NĂM HỌC 2023-2024
Môn: Toán - Lớp: 8
Thời gian làm bài: 120 phút
Câu 1. (2,0 điểm)
a) Phân tích đa thức thành nhân tử: x3 – 19x + 30
b) Cho x = by + cz ; y = ax + cz ; z = ax + by và x + y + z
≠
0; xyz
≠
0.
Chứng minh:
111
111abc
++
+++
= 2
Câu 2. (1,5 điểm)
a) Giải phương trình: 2(6x +7)2 (3x+ 4)(x + 1) – 12= 0
b) Tìm x, y nguyên thỏa mãn: x2 + 2y2 + 3xy – x – y + 3 = 0.
Câu 3. (3,0 điểm)
a) Tìm
,ab
sao cho
32
( ) 10 4f x ax bx x=++−
chia hết cho đa thức
2
() 2gx x x= +−
b) Tìm giá trị nhỏ nhất của biểu thức:
= ++ −− +
22
13 4 2 16 2019A x y xy y x
c) Chứng minh rằng:
32
33n nn− −+
chia hết cho
với mọi số nguyên lẻ
n
.
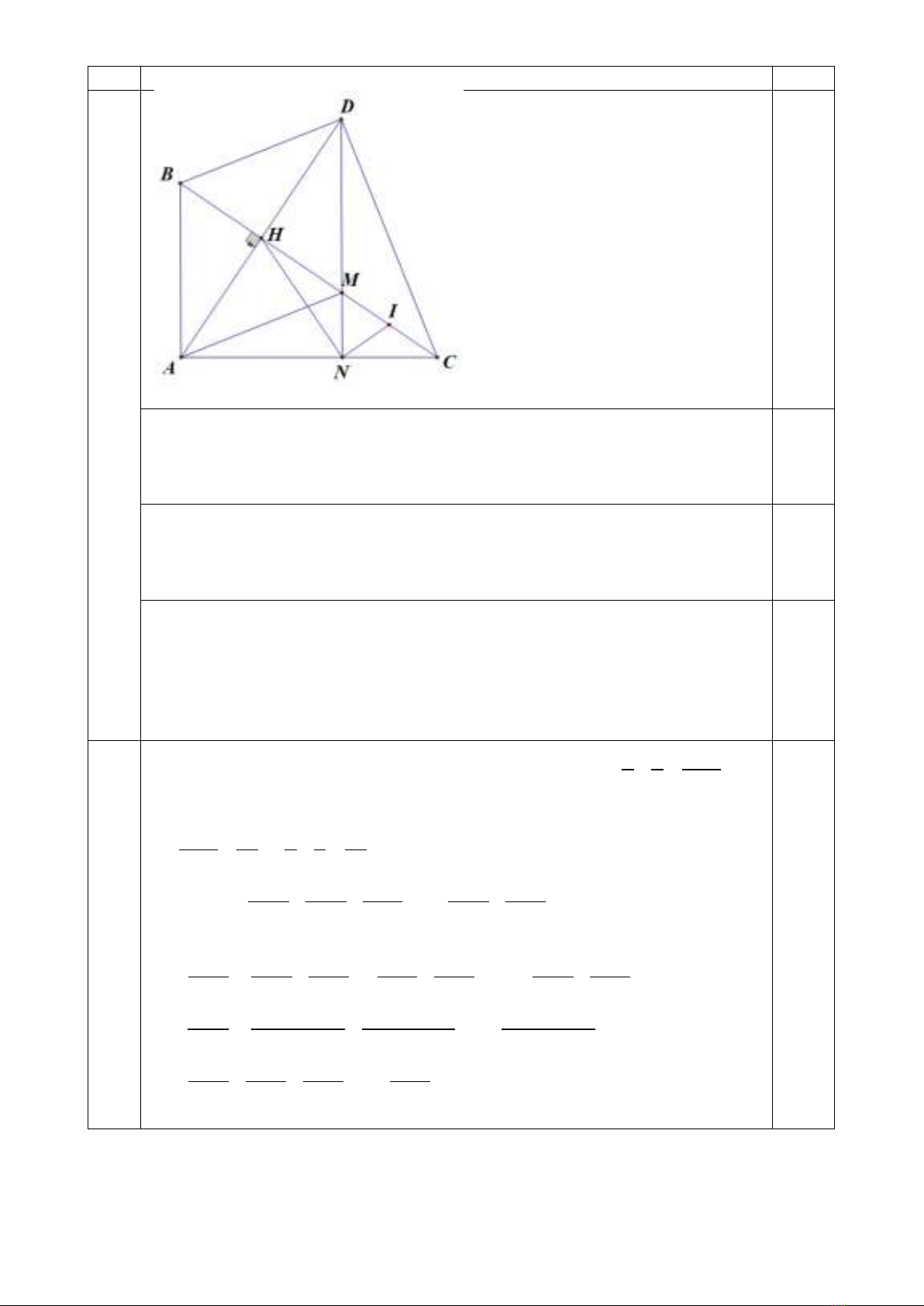
Câu 4. (3,0 điểm)
Cho tam giác
ABC
vuông tại
()A AB AC<
, đường cao
AH
. Gọi
D
là điểm
đối xứng của
A
qua
. Đường thẳng qua
song song với
AB
cắt
BC
và
AC
lần
lượt ở
M
và
.
a) Chứng minh tứ giác
ABDM
là hình thoi.
b) Chứng minh
AM
vuông góc với
CD
c) Gọi
I
là trung điểm của
MC
, chứng minh rằng
IN
vuông góc
HN
Câu 5. (0,5,0 điểm)
Cho a, b là các số thực dương khác nhau. Chứng minh
+>+
11 4
a b ab
Từ đó chứng minh
>1A
với
=+++++
111 11
...
2019 2020 2021 6054 6055
A
--------------------------- Hết ---------------------------
PHÒNG GD&ĐT TP BẮC GIANG
TRƯỜNG THCS SONG MAI
HƯỚNG DẪN CHẤM
ĐỀ KHẢO SÁT HỌC SINH GIỎI
NĂM HỌC 2023-2024
Môn: Toán - Lớp: 8
Dưới đây chỉ là sơ lược các bước giải và thang điểm. Bài giải của học sinh cần chặt
chẽ, hợp logic toán học. Nếu học sinh làm bài theo cách khác hướng dẫn chấm mà đúng
thì chấm và cho điểm tối đa của bài đó. Đối với bài hình học nếu học sinh vẽ sai hình hoặc
không vẽ hình thì không được tính điểm.
Câu
Hướng dẫn giải
Điểm
1
a) x3 – 19x + 30 = x3- 4x -15x - 30
= x(x2 - 4) - (15x - 30)
= x(x - 2)(x + 2) - 15(x - 2)
= (x - 2)(x2 – 2x - 15)
= (x - 2)(x2 + 3x – 5x – 15x)
= (x - 2)(x + 3)(x - 5)
0,25
0,25
0,25
0,25
b) Ta có x = by + cz (1); y = ax + cz (2); z = ax + by (3)
Cộng vế với vế của (1) và (2) ta có: x + y = ax + by + 2cx = z + 2cz
Suy ra: 2cz = x + y – z
c =
2
xyz
z
+−
⇒
1 + c =
2
xyz
z
++
1
1c+
=
2z
xyz++
Tương tự: 1 + a =
2
xyz
x
++
⇒
1
1a+
=
2x
xyz++
1 + b =
2
xyz
y
++
⇒
1
1b+
=
2y
xyz++
Vậy
1
1a+
+
1
1b+
+
1
1c+
=
2x
xyz++
+
2y
xyz++
+
2z
xyz++
=
)
(
2xyz
xyz
++
++
= 2
0,25
0,25
0,25
0,25
2
a) Ta có: 2(6x +7)2 (3x+ 4)(x + 1) – 12 = 0
( ) ( )( )
( ) ( )( )
2
2
2 6x 7 3x 4 x 1 12
6x 7 6x 8 6x 6 72
⇔ + + +=
⇔ + + +=
Đặt 6x + 7 = t, đẳng thức trên trở thành t2(t + 1)(t- 1) = 72
⇔
t2(t2 - 1) = 72
⇔
t4 - t2 - 72 = 0
⇔
(t2 +8)(t2- 9) = 0
⇔
t2 = 9 (Vì t2 + 8 dương)
⇔
t = 3 hoặc t = -3
Nếu t = 3 suy ra x = -
3
2
Nếu t = -3, suy ra x= -
3
5
Vậy x= -
3
2
hoặc x= -
3
5
0.25
0.25
0.25
b) Ta có: x2 + 2y2 + 3xy - x - y + 3 = 0.
⇔
.......
⇔
(x + y)(x + 2y - 1) = - 3
Vì x,y nguyên nên x + y và x + 2y - 1 là các ước của - 3.
Ta có bảng sau:
0.25
0.25
Câu
Hướng dẫn giải
Điểm
x + y
1
-3
-1
3
x + 2y -1
-3
1
3
-1
x
4
-8
-6
6
y
-3
5
5
-3
Vậy các cặp số nguyên (x; y) cần tìm là (4; 3), (-8;5), (-6; 5), (4; -3).
0.25
3
a)
32
( ) 10 4f x ax bx x=++−
;
2
() 2gx x x= +−
Ta có
( ) ( 1)( 2)gx x x=−+
Do
()fx
chia hết cho đa thức
()gx
nên
() ().()f x qx gx=
với
()qx
là đa thức
( ) ( 1)( 2). ( )f x x x qx=−+
Với
1x=
ta được
(1) 0f=
hay
60ab++=
Với
2x= −
ta được
( 2) 0f−=
hay
8 4 24 0ab−+ − =
2 60ab⇔− + − =
Khi đó ta có
6
26
ab
ab
+=−
− +=
4
2
a
b
= −
⇔= −
Vậy
4, 2ab=−=−
.
0, 5
0,25
0,25
b)
= ++ −− +
= +− + − + ≥
22
22
13 4 2 16 2019
(2 1) (3 2) 2014 2014
A x y xy y x
xy x
Min
=2014A
khi
−
= =
21
,
33
xy
0, 5
0,5
c) Ta có:
( ) ( )
32 3 2
3 3 33n nn nn n− −+= − − −
( ) ( )
22
13 1nn n= −− −
( )( ) ( )( )
11311nnn nn=−+−−+
( )( )( )
113nnn=−+−
Vì
n
lẻ nên.𝑛𝑛= 2𝑘𝑘+ 1 (𝑘𝑘 ∈ 𝑍𝑍)
Do đó
( )( )( ) ( )( )( )
1 1 3 211211213nnn k k k− + − = +− ++ +−
( )( )
2 2 22 2kk k= +−
( )( )
8 11kk k= +−
Vì
( )( )
11kk k+−
là tích của ba số nguyên liên tiếp nên
( )( )
11kk k+−
chia hết cho
2
và
3
.
Mà ƯCLN
( )
23 1,=
nên
( )( )
11kk k+−
chia hết cho
6
, suy ra
( )( )
8 11kk k+−
chia hết cho
48.
Vậy
32
33n nn− −+
chia hết cho
48
với mọi số nguyên lẻ
n
.
0,5
0,25
0,25
Câu
Hướng dẫn giải
Điểm
4
a) Chứng minh được
ABH DMH∆=∆
AB MD⇒=
mà
//AB MD
Nên
ABDM
là hình bình hành lại có 2 đường chéo vuông góc
Suy ra
ABDM
là hình thoi.
0,5
0, 5
0, 5
b) Sử dụng quan hệ từ vuông góc đến song song chứng minh được
DN AC⊥
Chứng minh được M là trực tâm của
ADC∆
Suy ra
AM
vuông góc với
CD
0,25
0,25
0,25
c) Sử dụng kiến thức trong tam giác vuông đường trung tuyến ứng với cạnh
huyền bằng nửa cạnh huyền.
Suy ra được
INC ICN MDH HNM= = =
Mà
90MNI INC+=°
90HNM MNI⇒ +=°
IN HN⇒⊥
0,25
0,25
025
5
*) Cho a, b là các số thực dương khác nhau. Chứng minh
+>+
11 4
a b ab
> ≠⇒− >⇒+ >
22
, 0, ( )0( )4a b a b a b a b ab
+
⇒ > ⇒+>
4 11 4ab
ab ab a b ab
*) Cho
=+++++
111 11
...
2019 2020 2021 6054 6055
A
Chứng minh rằng
>1A
Áp dụng câu a ta có
=+++++++
1 11 11 11
( ) ( ) ... ( )
2019 2020 6055 2021 6054 4037 4038
A
> + + ++
++ +
14 4 4
( ... )
2019 2020 6055 2021 6054 4037 4038
A
>++++
111 1
...
2019 2019 2019 2019
A
( có 2019 phân số)
⇒>1A
0,25
0,25