
UBND HUYỆN KỲ ANH
TRƯỜNG THCS KỲ TÂN
ĐỀ THI KSCL HSG HUYỆN LỚP 9 LẦN 1
Môn: Toán 9 - Năm học: 2023 - 2024
Thời gian: 120 phút (không kể thời gian giao đề)
PHẦN I: Thí sinh chỉ ghi kết quả vào bài làm
Bài 1.Tìm số hữu tỉ a, b thỏa mãn:
( ) ( )
2
1 3 1 3 0a b− + + + =
Bài 2. Rút gọn biểu thức:
( ) ( )
5 3
2 5 3 3 2 2
M+
= + + − −
Bài 3. Tìm tất cả các số nguyên dương n để
2
10n n
+
là số nguyên
Bài 4. Với giá trị nào của α thì Q = 3Sinα +
3 3 o. sQ sin c
α α
= +
đạt giá trị lớn nhất
Bài 5. Cho các số thực a,b thỏa mãn a+b=3 và ab=1. Tính
bbaa
baba
P
22
Bài 6. Giải phương trình:
2 2
4 20 25 4 4 1 20 20x x x x x+ + + − + = −
Bài 7. TiIm a, b sao cho sao cho đa thưJc
3 2
( ) . 10 4f x a x bx x= + + −
chia hêJt cho đa thưJc
2
( ) 2g x x x= + −
Bài 8. Cho tam giác ABC vuông tại A. Biết đường cao AH, trung tuyến CM, phân
giác trong BD đồng quy. Tính
AB
BC
.
Bài 9. Cho hình thang ABCD (AB//CD) gọi O là giao điểm hai đường chéo. Biết
SAOB=4cm2; SCOD=9cm2. Tính diện tích hình thang ABCD.
Bài 10. Hai đội cờ thi đấu với nhau. Mỗi đấu thủ của độ này thi phải đấu một ván với
tất cả đấu thủ của đội kia. Biết rằng tổng số ván cờ đã thi đấu bằng 4 lần tổng số đấu
thủ của hai đội và biết rằng số đấu thủ của một trong hai đội là số lẻ. Hỏi mỗi đội có
bao nhiêu đấu thủ?
PHẦN II: Thí sinh trình bày lời giải.
Bài 11.
a) Giải phương trình:
2 2 2
2 3 2x x x x x+ − + = + +
b) Tìm tất cả các cặp số nguyên (x ; y) thoea mãn
2 4 3 2
y y x x x x+ = + + +
Bài 12. Cho hình chữ nhật ABCD. Đường thẳng qua C vuông góc góc với AC cắt AB
và AD lần lượt tại E và F. Gọi I là trung điểm của EF.
a) Chứng minh AI
⊥
BD
b) Chứng minh
BE CF DF CE BD EF+ =
Bài 13. Cho a, b laI caJc số thực không âm thoea mann
1a b+ =
. Tìm giá trị nhoe nhâJt vaI
giaJ trio lớn nhất của
2 2
1 4
1 1
ab
Pa b
= +
+ +
Hết
Họ và tên: …………………………………………..; SBD: ……………..
Lưu ý: Thí sinh không được sử dụng máy tính.
HƯỚNG DẪN CHẤM
PHẦN I: Phần ghi kết quả (10 điểm)
Bài Bài 1 Bài 2 Bài 3 Bài 4 Bài
5Bài 6 Bài 7 Bài 8 Bài 9 Bài 10
KQ a = 2,
b = -6 M =-1 n = 8 α= 600
P =
3
2
3
2
x=
a=-4
b=-2
5 1
2
−
25 5 và 20
PHẦN II. Phần trình bày lời giải (10 điểm)
Bài Nội dung Điểm
Bài 11 (4đ)
a)
Giải phương trình:
2 2 2
2 3 2x x x x x+ − + = + +
2 2 2
2 2 3x x x x x + − + − + =
2 2
2 2 2( 1) 2 6x x x x + − + + =
2 2 2
2 1 2( 1) 2 2 9x x x x x + + − + + + + =
()
2
2
1 2 9x x + − + =
2
2
1 2 3
1 2 3
x x
x x
+ − + =
+ − + = −
+)
2 2
1 2 3 2 2x x x x+ − + = − = +
( 2)x>
2 2
1
4 4 2 2
x x x x − + = + =
(loại)
+)
2 2
1 2 3 4 2x x x x+ − + = − + = +
( 4)x> −
2 2
7
8 16 2 4
x x x x + + = + = −
(thỏa mãn)
Vậy phương trình có nghiệm duy nhất
7
4
x= −
2 điểm
b)
Ta có
( )
( )
( ) ( )
( )
( )
( )
2 4 3 2 2 4 3 2
2
22
2
22
4 4 1 4 4 4 4 1
2 1 2 3 1 1
2 1 2 1 2
y y x x x x y y x x x x
y x x x x
y x x x x
+ = + + + + + = + + + +
+ = + + + +
+ = + + − −
Ta thấy rằng khi x<-1 hoặc x>2 thì (3x+1)(x+1)>0 và x(x-2)>0
Nên
( )
( )
( )
2 2
2
2 2
2 2 1 2 1x x y x x+ < + < + +
(*) Loại vì không có số
nguyên y thỏa mãn.
Do đó -1≤x≤2 suy ra
{ }
1;0;1;2x −
Lần lượt thay các giá trị của x tìm được các giá trị của y
Vậy phương trình đã cho có 6 nghiệm nguyên là:
(x; y)=(0,5), (2 6), (0 : 0), (0; 1), ( 1,0),( 1, 1)
2 điểm
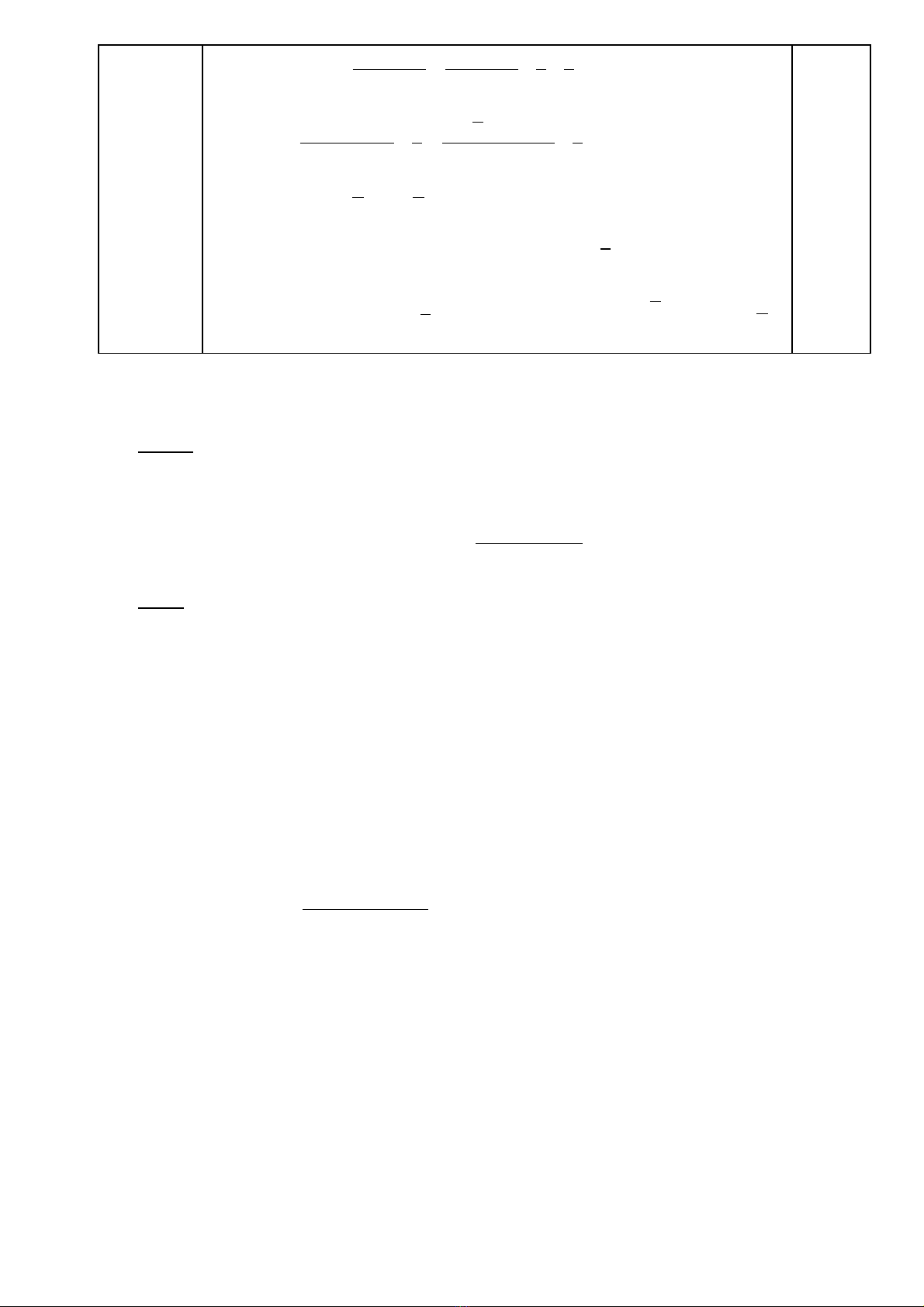
Bài 12 (4 điểm)
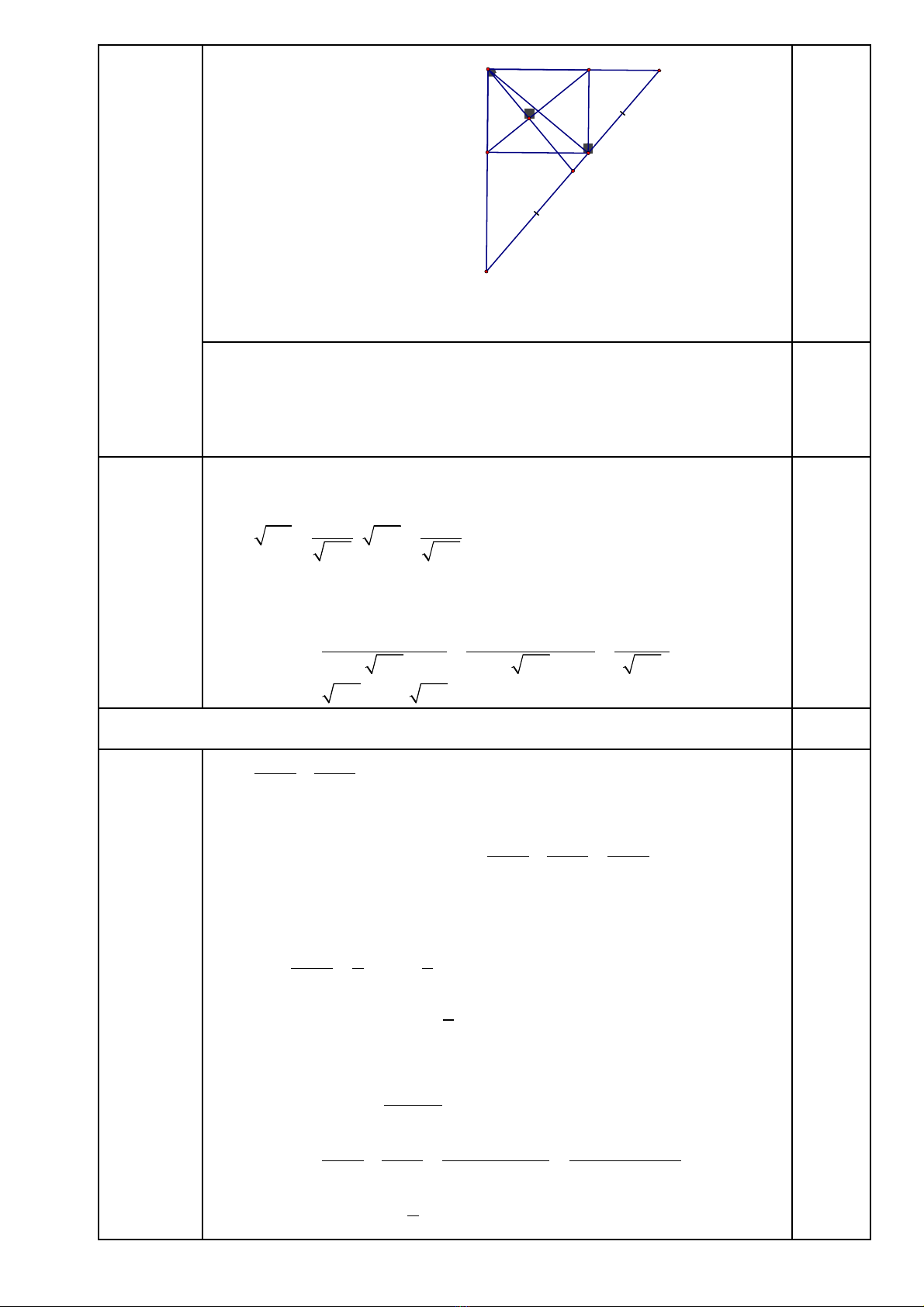
a)
Chứng minh được AB.AE=AD.AF (=AC2)
suy ra hai tam giác ABD và AFE đồng dạng
suy ra
ADB AEF =
mà
0
IAF AF ; AF AEF 90I I = + =
nên
0
IAF 90ADB + =
nên AI
⊥
BD
2 điểm
b)
Áp dụng hệ thức lượng trong tam giác vuông AEF với đường
cao AC ta có: AE2=EF.CE; AF2=EF.CF
nên
;
AE AF
CE CF
EF EF
= =
và các tam giác BEC đồng dạng với CAF, DCF đồng dạng với
CEA
suy ra
.AF DF.AE . . .EF
.
BE AC EC AC CF AC
VT EF EF EF
AC EF BD EF VP
+ +
= = =
= = =
2 điểm
Bài 13 (2 điểm)
2 2
1 4
1 1
ab
Pa b
= +
+ +
TiIm GTNN
Do
2 2 2
1 4 1
, 0 . 0 1 1 1
ab
a b a b P a b a
+ = + + +
Theo baIi ra
2 2
, 0 0 1 1 1 2
1
a b a a a
a b
+
+ =
2
1 1 1
1 2 2
P
a
+
. DâJu “=” xâey ra khi a=1, b=0
Vâoy GTNN cuea
1
2
P=
TiIm GTLN
Ta coJ
2
( )
4 4. 1
4
a b
ab +
=
2 2
2 2 2 2 2
1 1 2 3 2
1 1 ( 1)( 1) ( ) 2 2
a b ab
Pa b a b ab ab
+ + −
= = +
+ + + + − +
Đăot
1
;0 4
ab t t=
2 điểm
H
I
F
E
B
D
C
A
Ta coJ
2 2
3 2 3 2 8 8
2 2 2 2 5 5
t t
Pt t t t
− −
= − +
− + − +
2
2 2
1
( )( 8 4)
8 6 1 8 8
4
5( 2 2) 5 5( 2 2) 5
t t
t t
Pt t t t
− − +
− + −
+ = +
− + − +
Do
1 1
0 0; 8 4 0
4 4
t t t − − + >
Măot khaJc
2 2
2 2 ( 1) 1 0t t t− + = − + >
Nên
8
5
P
Vâoy GTLN cuea
8
5
P=
. DâJu băIng xâey ra khi
11
42
1
ab a b
a b
=
= =
+ =
Lưu ý: mọi cách giải đúng đều cho điểm tối đa
Bài 1: Cho đa thức bậc 4 f(x) với hệ số bậc cao nhất là 1 và thoả mãn :
f(1) = 10, f(2)= 20, f(3) =30
Tính giá trị của biểu thức A=
(12) ( 8) 34
10
f f+ − +
Giải:
Đặt g(x) = f(x) – 10x
g(1) = g(2) = g(3) = 0
g(x) có 4 nghiệm là 1, 2, 3, 4. Mặt khác do bậc g(x) là bậc 4 và hệ số cao nhất
là 1 nên ta có: g(x) = (x – 1)(x – 2)(x – 3)(x – x0)
Suy ra f(x) =(x – 1)(x – 2)(x – 3)(x – x0) +10x
Thay vào ta có : f(12) = 11.10.9.(12-x0)+120 =12.11.10.9 – 990.x0 + 120
f(-8) = (-9).(-10).(-11).(-8-x0) - 80 = 8.11.10.9 + 990.x0 - 80
Vậy A =
(12) ( 8) 32 1984 32 2016
10
f f
+ − + = + =


























