Mã đề 101 Trang 1/7
SỞ GD&ĐT THANH HOÁ
TRƯỜNG THPT NGUYỄN QUÁN NHO
--------------------
(Đề thi có 07 trang)
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LỚP 12 – LẦN 3
NĂM HỌC 2023 – 2024
MÔN: TOÁN
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Họ và tên: ...................................................................
Số báo danh: ..................
Mã Đề: 101.
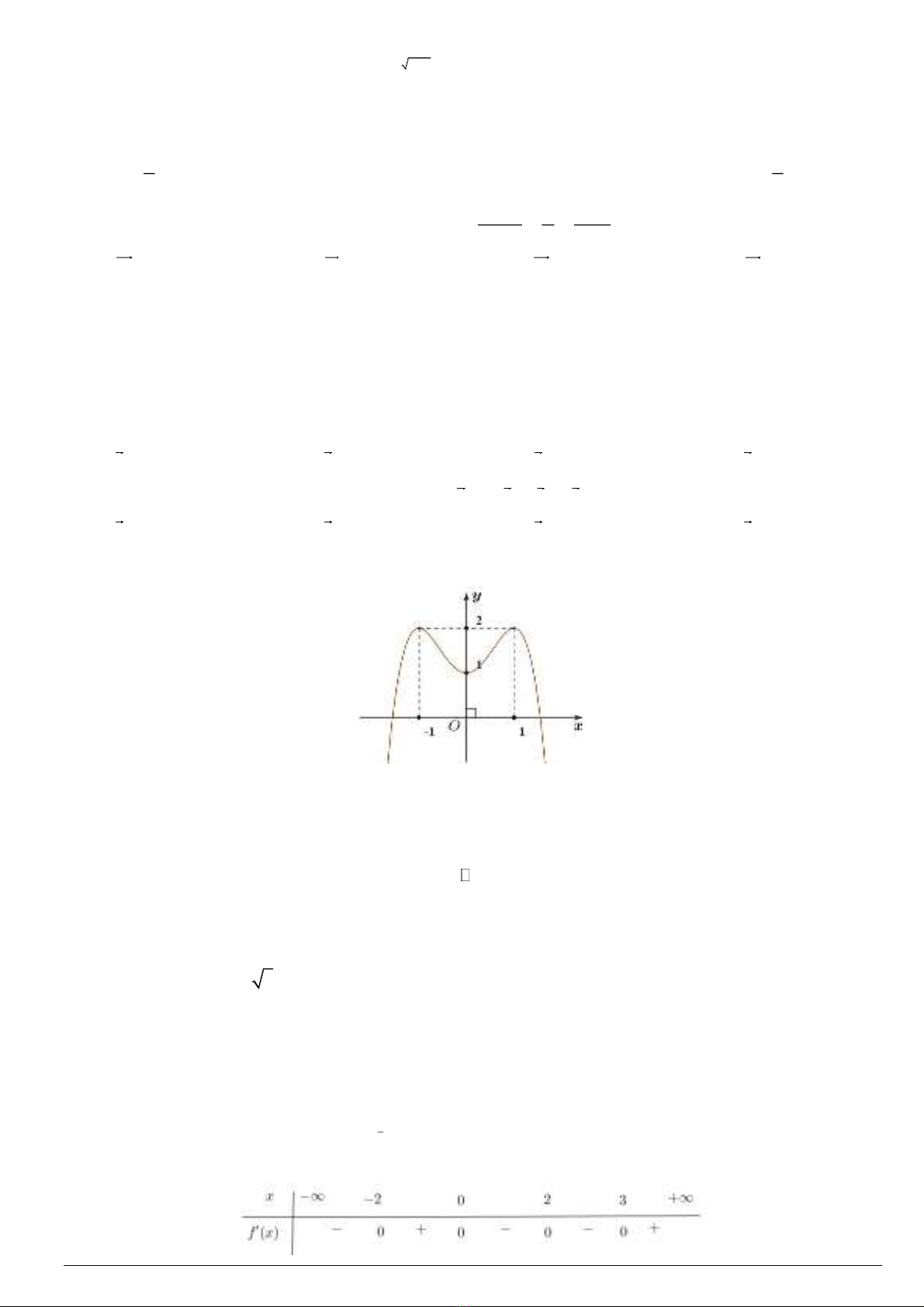
Câu 1. Cho hàm số
y f x
có bảng biến thiên như sau:
Phương trình đường tiệm cận ngang của đồ thị hàm số là:
A.
3.x
B.
2.y
C.
2.x
D.
3.y
Câu 2. Cho hình trụ có diện tích xung quanh bằng
16
và độ dài đường sinh bằng đường kính của đường tròn
đáy. Bán kính
r
của hình trụ đã cho bằng:
A.
2
. B. 4. C.
22
. D. 2.
Câu 3. Có bao nhiêu cách xếp 6 học sinh thành một hàng dọc?
A. 6. B. 1. C. 36. D. 720.
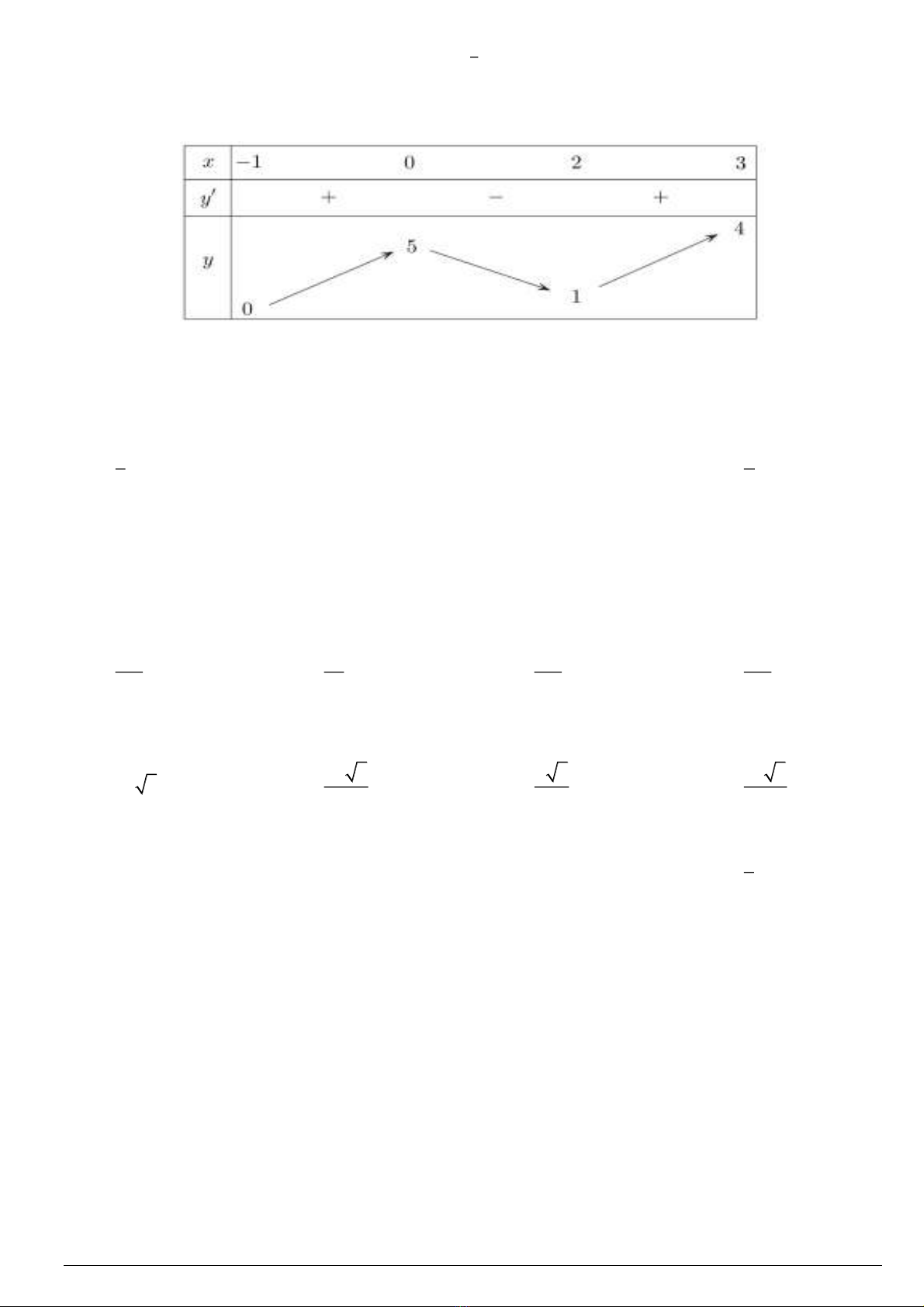
Câu 4. Cho hàm số
fx
xác định trên và có bảng xét dấu của đạo hàm
fx
như sau:
Giá trị cực đại của hàm số
fx
bằng:
A.
1f
. B.
3f
. C.
1f
. D.
4f
.
Câu 5. Ham sô
fx
co
2 2, 3 5ff
; ham sô
'y f x
liên tu
c trên
2;3
. Khi đo
3
2
'f x dx
băng:
A. −3. B. 3. C. 7. D. 10.
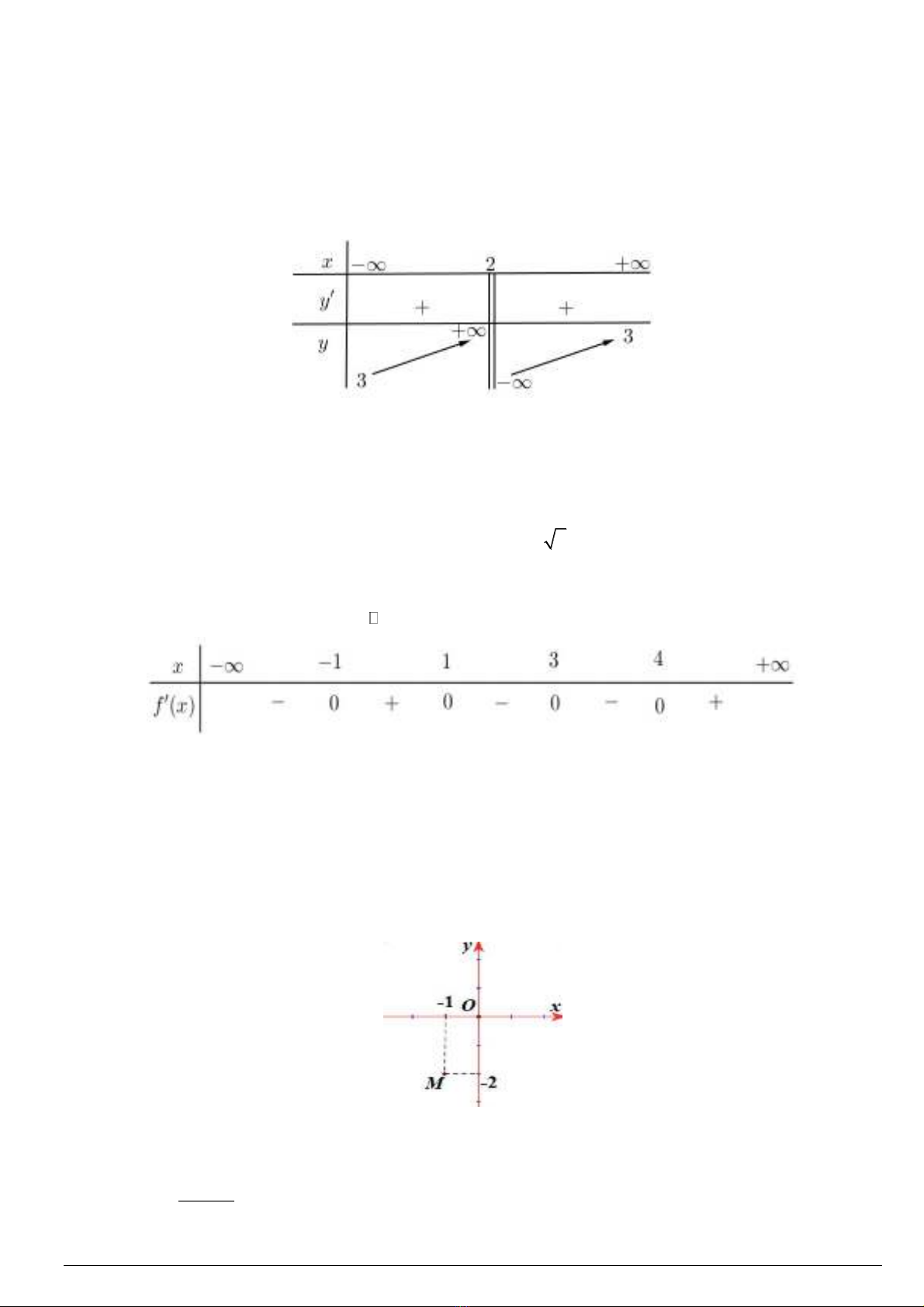
Câu 6. Điểm
M
trong hình sau là điểm biểu diễn của số phức nào dưới đây?
A.
12i
. B.
2i
. C.
2i
. D.
12i
.
Câu 7. Cho
2023xdx F x C
. Khẳng định nào dưới đây đúng?
A.
2023
ln 2023
x
Fx
. B.
2022x
Fx
.
C.
2023 .ln 2023
x
Fx
. D.
2023x
Fx
.