SỞ GD VÀ ĐT TPHCM ĐỀ THI THỬ VÀO LỚP 10 NĂM HỌC 2018-2019
ĐỀ MINH HỌA SỐ 20 MÔN: TOÁN
Đề thi gồm 2 trang Thời gian làm bài :120 phút ( không tính thời gian phát đề)
Bài 1:
a) Viết phương trình đường thẳng (d) song song với đường thẳng y = 3x + 1 và cắt trục tung tại điểm có tung
độ bằng 4.
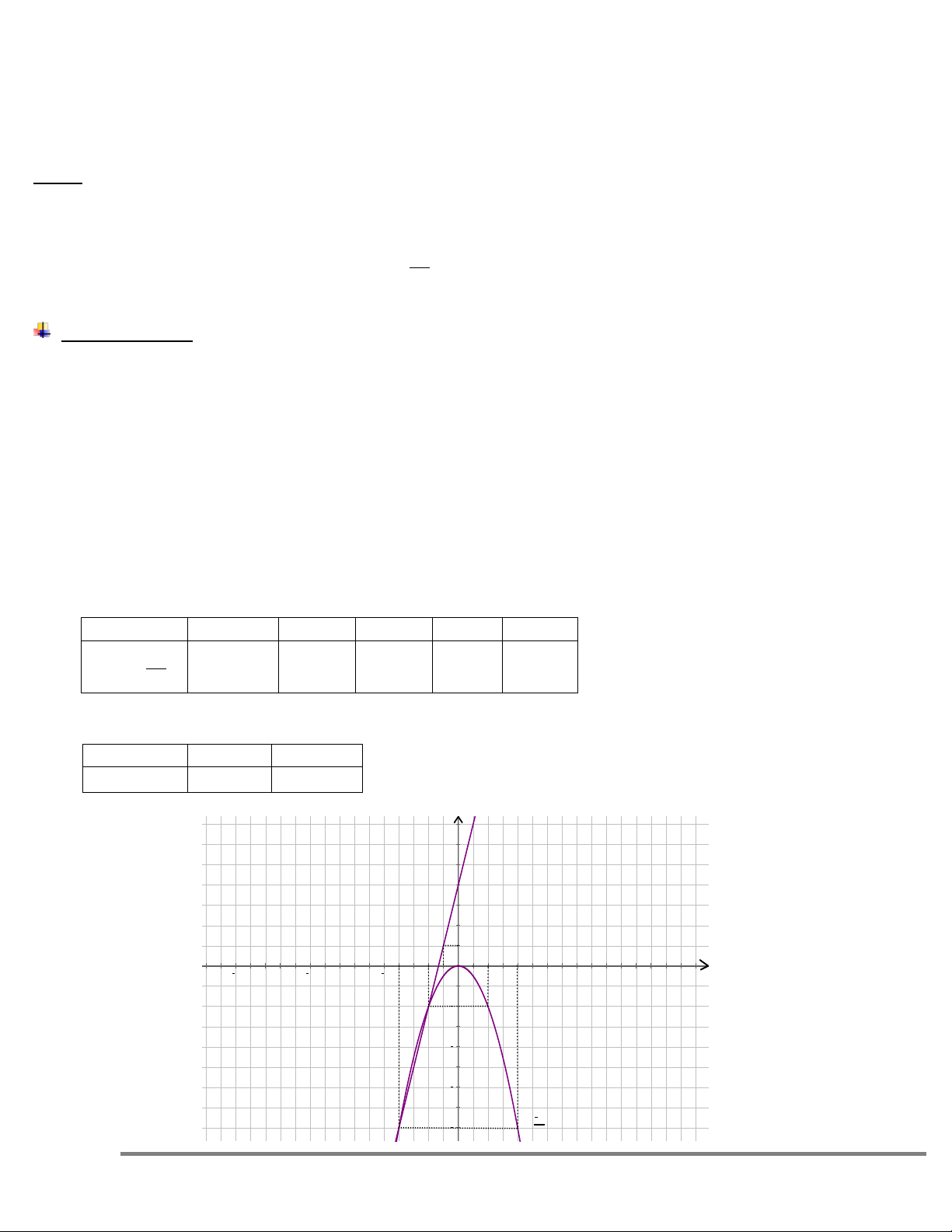
b) Vẽ đồ thị hàm số y = 3x + 4 và
2
2
x
y
trên cùng một mặt phẳng tọa độ. Tìm tọa độ các giao điểm của
hai đồ thị ấy bằng phép tính.
Bài 2: Cho phương trình:
210 x mx
(1) (x là ẩn số)
a) Chứng minh phương trình (1) luôn có 2 nghiệm.
b) Gọi x1, x2 là các nghiệm của phương trình (1). Tính giá trị của biểu thức:
22
11 22
12
11
 

xx xx
Pxx
Bài 3: Cho tam giác ABC có 3 góc nhọn và AB < AC. Đường tròn tâm O đường kính BC cắt các cạnh AB, AC
theo thứ tự tại E và D. Gọi H là giao điểm của BD và CE, gọi K là giao điểm của AH và BC. Từ A kẻ các
tiếp tuyến AM, AN đến đường tròn (O) với M, N là các tiếp điểm. Cho biết góc ANM = 300. Tìm số đo
góc AKN?
Bài 4: Các nhà khoa học về thống kê đã thiết lập được hàm số để tính về độ tuổi trung bình
các phụ nữ kết hôn lần đầu của thế giới như sau: A(t) = 0,08t + 19,7. Trong đó: A(t)
là tuổi trung bình các phụ nữ kết hôn lần đầu của thế giới, t là năm kết hôn với gốc
thời gian tính từ năm 1950 nghĩa là năm 1950 thì t = 0, năm 1951 thì t = 1,…
a) Hãy tính độ tuổi trung bình các phụ nữ kết hôn lần đầu trên thế giới lần lượt vào các
năm 1980, 2005.
b) Vào năm mà đội tuyển U23 Việt Nam lọt vào chung kết U23 Châu Á và giành huy
chương Bạc thì độ tuổi trung bình các phụ nữ kết hôn lần đầu trên thế giới là bao nhiêu?
c) Vào năm bao nhiêu thì độ tuổi trung bình các phụ nữ kết hôn lần đầu là 25,7 tuổi?
Bài 5: Trên nóc một toàn nhà có một cột ăg-ten thẳng cao 4m. Từ vị trí
quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân
C của cột ăng-ten lần lượt dưới góc 500 và 400 so với phương nằm
ngang (như hình vẽ bên)
Tính chiều cao CH của tòa nhà (kết quả làm tròn đến chữ số
thập phân thứ ba).
Bài 6:
a) Ông Sáu gửi một số tiền vào ngân hàng theo mức lãi suất tiết kiệm
với kỳ hạn 1 năm là 6%. Tuy nhiên, sau thời hạn 1 năm ông Sáu
không đến nhận tiền lãi mà để thêm một năm nữa mới lãnh. Khi đó, số tiền lãi có được sau năm đầu tiên
40°
50°
4m
7m
FH
D
C
B
A
sẽ được ngân hàng cộng dồn vào số tiền gửi ban đầu để thành số tiền gửi cho năm kế tiếp với mức lãi suất
như cũ. Sau hai năm, ông Sáu nhận được tất cả số tiền là 112 360 000 đồng (kể cả gốc và lãi). Hỏi ban
đầu ông Sáu đã gửi bao nhiêu tiền? (trích đề thi tuyển sinh 10 TPHCM năm 2016)
a) Anh Tường có một miếng đất hình chữ nhật, chiều dài là 90m và chiều rộng là 50m. Anh Tường chia
miếng đất ra thành những miếng đất nhỏ hình vuông để trồng các loại rau trên từng miếng đất hình vuông
đó. Hỏi số miếng đất hình vuông mà anh Tường chia được ít nhất là bao nhiêu? (biết độ dài cạnh miếng
đất hình vuông là một số tự nhiên)
Bài 7: Mẹ Quân đang có một chậu chứa 4 lít dung dịch nước muối nồng độ 2% dùng để
rửa rau. Tuy nhiên, mẹ muốn rửa thêm một ít rau nữa cho cô Tư hàng xóm nên
mẹ nhờ Quân cho thêm vào chậu 2 muỗng muối và sau đó cho thêm vào chậu
một lượng nước tương ứng 1,5 lít nữa. Biết mỗi muỗng muối chứa khối lượng
muối tương ứng là 10 gam và 1 lít nước có khối lượng tương ứng là 1kg. Hãy tìm
nồng độ muối của chậu nước sau khi Quân pha thêm?
Bài 8: Khoảng cách từ nhà ga xe lửa A đến thị trấn C là
78km. Hỏi nếu đi dọc theo đường sắt AB đến trạm
trung chuyển M rồi đi xe theo đường bộ đến thị
trấn C thì mất thời gian bao lâu? Biết trạm trung
chuyển M cách nhà ga A là 32km, vận tốc của tàu
trên đường sắt là 80km/h và của xe chạy trên
đường bộ là 50km/h, góc CMB = 300 (làm tròn kết
quả đến chữ số hàng đơn vị).
Bài 9: Để tặng thưởng cho các học sinh đạt thành tích trong kỳ thi học sinh giỏi
Toán lớp 9. Nhà trường đã trao 30 phần thưởng cho các học sinh với tổng giá
trị giải thưởng là 2 700 000 đồng. Trong đó bao gồm: mỗi học sinh đạt giải
nhất được thưởng 150 000 đồng, học sinh đạt giải nhì được thưởng 130 000
đồng, giải ba được thưởng 100 000 đồng, học sinh đạt giải khuyến khích
được thưởng 50 000 đồng. Biết rằng, có 10 giải ba và ít nhất một giải nhì
được trao. Hỏi nhà trường đã trao bao nhiêu giải nhất, nhì và khuyến khích?
Bài 10: Một con quạ đang khát nước. Nó bay rất lâu để tìm nước nhưng
chẳng thấy một giọt nước nào. Mệt quá, nó đậu xuống cành cây
nghỉ. Nó nhìn xung quanh và bỗng thấy một cái ly nước ở dưới một
gốc cây. Khi tới gần, nó mới phát hiện ra rằng cái ly nước có dạng
hình trụ: chiều cao là 15cm , đường kính đáy là 6cm , lượng nước
ban đầu trong ly chỉ cao 5cm , cho nên nó không thể uống được
nước. Nó thử đủ cách để thò mỏ được đến mặt nước, nhưng mọi cố
gắng của nó đều thất bại. Nó nhìn xung quanh, nó thấy những viên
sỏi hình cầu có cùng đường kính là 3cm nằm lay lắt ở gần đấy. Lập tức, nó dùng mỏ gắp 15 viên sỏi thả
vào ly. Hỏi sau khi thả 15 viên sỏi, mực nước trong ly cách miệng ly bao nhiêu cm ?
(P/S: chuyện hơi ly kỳ một tí, mong các bạn đừng “ném đá”, hãy chỉ chú ý đến kiến thức Toán trong câu
chuyện).
- HẾT-
32km
78km
30°
B
C
M
A
BÀI GIẢI CHI TIẾT
Bài 1:
a) Viết phương trình đường thẳng (d) song song với đường thẳng y = 3x + 1 và cắt trục tung tại điểm có
tung độ bằng 4.
b) Vẽ đồ thị hàm số y = 3x + 4 (d) và
2
2
x
y
(P) trên cùng một mặt phẳng tọa độ. Tìm tọa độ các giao
điểm của hai đồ thị ấy bằng phép tính.
Bài giải chi tiết:
a)
Giả sử phương trình đường thẳng (d) có dạng: y = ax + b (1) với
0a
.
Do (d) song song với đường thẳng y = 3x + 1 nên suy ra:
3
1
a
b
Mặt khác, (d) cắt trục tung tại điểm có tọa độ x = 0; y = 4.
Thế x =0, y = 4, a = 3 vào phương trình (1), ta được:
4 3.0 4bb
(thỏa mãn
1b
)
Vậy phương trình đường thẳng (d) cần tìm là: y = 3x + 4
b)
Bảng giá trị:
x
-4
-2
0 2 4
2
2
x
y
-8
-2
0
-2
-8
Đồ thị hàm số (P) đi qua các điểm:
4; 8 , 2; 2 , 0;0 , 2; 2 , 4; 8
.
x
0
34yx
4
Đường thẳng (d) đi qua các
điểm:
0;4
và
1;1
.
Đồ thị.
6
4
2
2
4
6
8
15 10 5 5 10 15
-1
1
4
2
-4 -2 x
y
y = 3∙x + 4
y = x2
2
Phương trình hoành độ giao điểm của (P) và (d) là:
2 2 2 2
13 4 6 8 6 8 0 4 2 8 0
2
4 2 4 0 4 . 2 0
4 0 4
2 0 2
x x x x x x x x x
x x x x x
xx
xx




Với x = -2 thế vào phương trình (d):
34yx
, ta được: y = -2
Với x = -4 thế vào phương trình (d):
34yx
, ta được: y = -8
Vậy: (d) cắt (P) tại hai điểm
2; 2
và
4; 8
.
Nhận xét:
Ở câu a, có lẽ cũng nhiều em còn lúng túng hoặc bị quên kiến thức. Tôi sẽ nhắc lại về lý thuyết cho
các em nhớ và vận dụng:
Cho: Đường thẳng (d) có phương trình: y = ax + b (với
0a
)
Đường thẳng (D) có phương trình: y = a’x + b’ (với
'0a
)
+ Hai đường thẳng (d) và ( D) cắt nhau
'aa
+ Hai đường thẳng (d) và ( D) song song
'
'
aa
bb
+ Hai đường thẳng (d) và ( D) trùng nhau
'
'
aa
bb
Bài 2: Cho phương trình:
210 x mx
(1) (x là ẩn số)
a) Chứng minh phương trình (1) luôn có 2 nghiệm.
b) Gọi x1, x2 là các nghiệm của phương trình (1). Tính giá trị của biểu thức:
22
11 22
12
11
 

xx xx
Pxx
Bài giải chi tiết:
a)
Phương trình: x2 – mx – 1 = 0 có a = 1; b = -m; c = -1
Ta có:
2
22
4 4.1. 1 4 0b ac m m
với mọi m.
phương trình luôn có hai nghiệm phân biệt với mọi m.
b)
Cách 1: Theo hệ thức vi-et ta có:
12
12
1
1
.1
1
bm
x x m
a
c
xx a
Ta có:
22
11 22
12
22
2 1 1 1 2 2
12
22
1 2 1 2 2 1 2 1 2 1
12
1 2 1 2 1 2
12
1 2 1 2
12
12
12
12
12
12
11
. 1 . 1
.
. . . .
.
..
.
. . 1
.
. 1 1 : . 1
.
.0
.
0
xx xx
Pxx
x x x x x x
xx
x x x x x x x x x x
xx
x x x x x x
xx
x x x x
xx
xx do x x
xx
xx
xx
 


Cách 2:
Do x1 là nghiệm của (1)
22
1 1 1 1
1 0 1x mx x mx
(*)
Do x2 là nghiệm của (1)
22
2 2 2 2
1 0 1x mx x mx
(**)
Thế (*) và (**) vào biểu thức
22
11 22
12
11
 

xx xx
Pxx
Ta được:
22
11 22
12
1 1 2 2
12
12
12
11
1 1 1 1
11
1 1 0
xx xx
Pxx
mx x mx x
xx
x m x m mm
xx
 



Nhận xét: