PHÒNG GIÁO DỤC VÀ ĐÀO TẠO THANH CHƢƠNG
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG NĂM HỌC 2019 – 2020
VÀ THI THỬ VÀO LỚP 10 THPT.
Môn thi: TOÁN 9
Thời gian: 120 phút (không kể thời gian giao đề)
Câu 1. (2,0 điểm)
1. T nh: A
( 6 3) 3 ( 2 3)
2. Rút g n iểu th :
3 x x 3
Bx9
x 3 x 3
Câu 2. (2,0 điểm)
Cho phƣơng trình: x2 – 2(m + 1)x + m2 – 3 = 0. (1) (Với m là tham số)
a. Giải phƣơng trình khi m -1
. Tìm giá trị ủa m để phƣơng trình (1) ó 2 nghiệm , và iểu th
1 2 1 2
x ( 6) 3( )P x x x
đạt giá trị nhỏ nhất
Câu 3. (1,5 điểm):
Vừa qua, hội đồng đội huyện Thanh Chƣơng đã tổ h ho 128 đại iểu đại diện
ho hơn mƣơi h n ngàn đội viên trên toàn huyện về tham dự Đại hội đại iểu háu
ngoan Bá Hồ lần th XII năm 2020 trên quê hƣơng Kim Liên – Nam Đàn. Ban tổ h
đã ố tr ho 128 đại iểu ngồi đều trên á xe nhƣ sau: Nếu dùng loại xe lớn hở hết
một lƣợt số đại iểu thì phải điều t hơn nếu dùng loại xe nhỏ là 4 hiế , iết rằng loại
xe lớn hở nhiều hơn loại xe nhỏ là 16 đại iểu. T nh số xe lớn nếu số xe đó đƣợ dùng
hở đại iểu háu ngoan Bá Hồ?
Câu 4. (3,5 điểm)
Cho đƣờng tròn tâm O án k nh R. Hai đƣờng k nh AB và CD ố định vuông góc
với nhau ủa đƣờng tròn (O). M là một điểm di động trên ung nhỏ AC; MD ắt AB tại
E.
a. Ch ng minh: T giá OCME nội tiếp
. Ch ng minh: DM.DE = 2R2
c. Nối MB ắt AC tại F. Ch ng minh: F là tâm đƣờng tròn nội tiếp tam giá MEC
d. Tìm vị tr ủa điểm M trên ung nhỏ AC để ME.ED đạt giá trị lớn nhất
Câu 5.(1,0 điểm):
Giải phƣơng trình:
2 2 2
( 2) 4 2 4x x x x
-------------------------Hết---------------------------
Chú ý: Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: ........................................................Số báo danh: ..........................
ĐỀ CHÍNH THỨC
(Đề thi gồm 1 trang)

HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
Câu
Ý
Nội dung cần đạt
Điểm
1
a
A =
( 6 3) 3 ( 2 3) 3 2 3 2 3 2 2
1.0
2.0
b
3 x x 3
Bx9
x 3 x 3
3( x 3) x( x 3) x 3
x9
( x 3)( x 3) ( x 3)( x 3)
3 x 9 x 3 x x 3
x9
( x 3)( x 3)
9 x x 3 1
x9
( x 3)( x 3) x 3
0.25
0.25
0.25
0,25
2
a
Thay m = - 1vào pt(1) ta đƣợ : x2 – 2 = 0
suy ra
2x
0.25
0.25
2.0
b
Cho phƣơng trình: x2 – 2(m + 1)x + m2 – 3 = 0
HS t nh đúng:
'24m
Để pt ó hai nghiệm phân iệt thì
' 0 2m 4 0 m 2
Với
m2
pt ó hai nghiệm x1, x2 thỏa mãn hệ th Vi-ét
12
2
12
2( 1)
.3
x x m
x x m
Thay vào
1 2 1 2 1 2 1 2
x ( 6) 3( ) 3( )P x x x x x x x
Ta đƣợ
22
3 6( 1) m 6 3 ( 2) 4( 2) 5P m m m m m m
Với
m 2 2 0m
Suy ra
5P
Vậy GTNN ủa P -5 khi m=-2
0.25
0.25
0.25
0.25
0.25
0.25
3
HS h n đúng ẩn, đặt điều kiện
(G i số xe lớn đƣợ dùng để hở đại iểu là x (xe)
*xN
HS lập luận để lập đúng phƣơng trình:
128 128 16
4xx
HS giải đúng phƣơng trình đƣợ : x = 4(t/m) ; x= -8 ( loại)
HS kết luận đúng số xe lớn là 4 xe
0.25
0.5
0.5
0.25
1.5
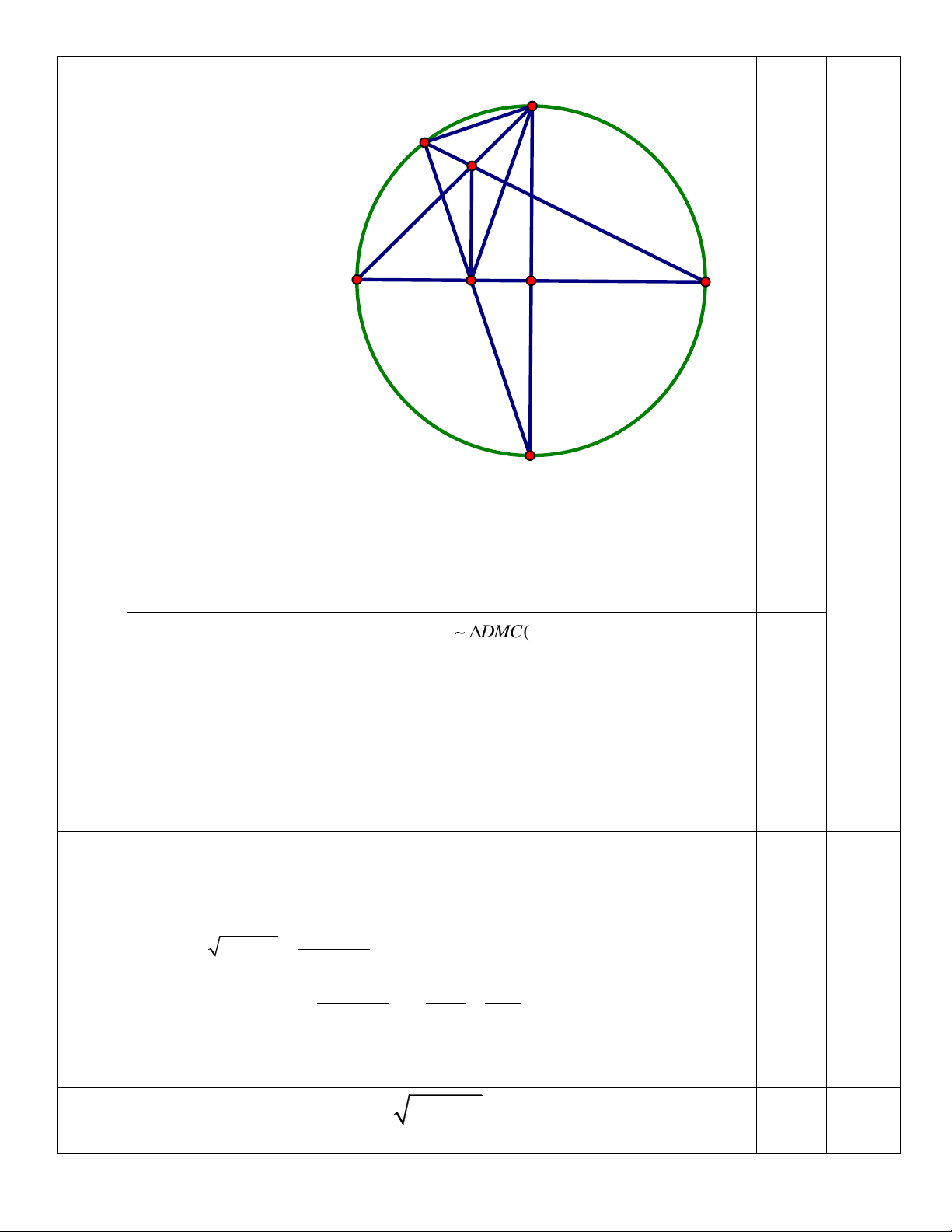
HS vẽ hình đúng
0.5
4
F
E
D
C
A
O
B
M
a
HS h ng minh đƣợ
90o
CMD
(gó nội tiếp hắn nửa đƣờng
tròn),
90o
COE
(hai đƣờng k nh vuông gó )
Ch ng minh đƣợ : T giá MEOC nội tiếp
0.5
0.5
3.5
b
HS h ng minh đƣợ
( . )DOE DMC g g
HS suy ra đƣợ
2
. . 2DE DM DO DC R
0.5
0.5
c
HS ch ng minh đƣợ t giá MAEF( vì
0
45FME FAE
) rồi
suy ra đƣợ t giá BCFE nội tiếp
suy ra đƣợ : F là giao điểm ủa á đƣờng phân giá trong
ủa tam giá MCE, từ đó suy ra F là tâm đƣờng tròn nội tiếp
tam giác MEC
0.25
0.25
d
HS hỉ ra đƣợ ME.ED lớn nhất khi và hỉ khi ME + ED lớn
nhất.
Áp dụng ất đẳng th Cosi ta có:
222
2
.2
.2 4 4
ME ED
ME ED
ME ED MD CD
ME ED R
ME.ED đạt GTLN ằng R2 khi
ME ED MC
MD CD
0.25
0.25
5
2 2 2
( 2) 4 2 4x x x x
(1)
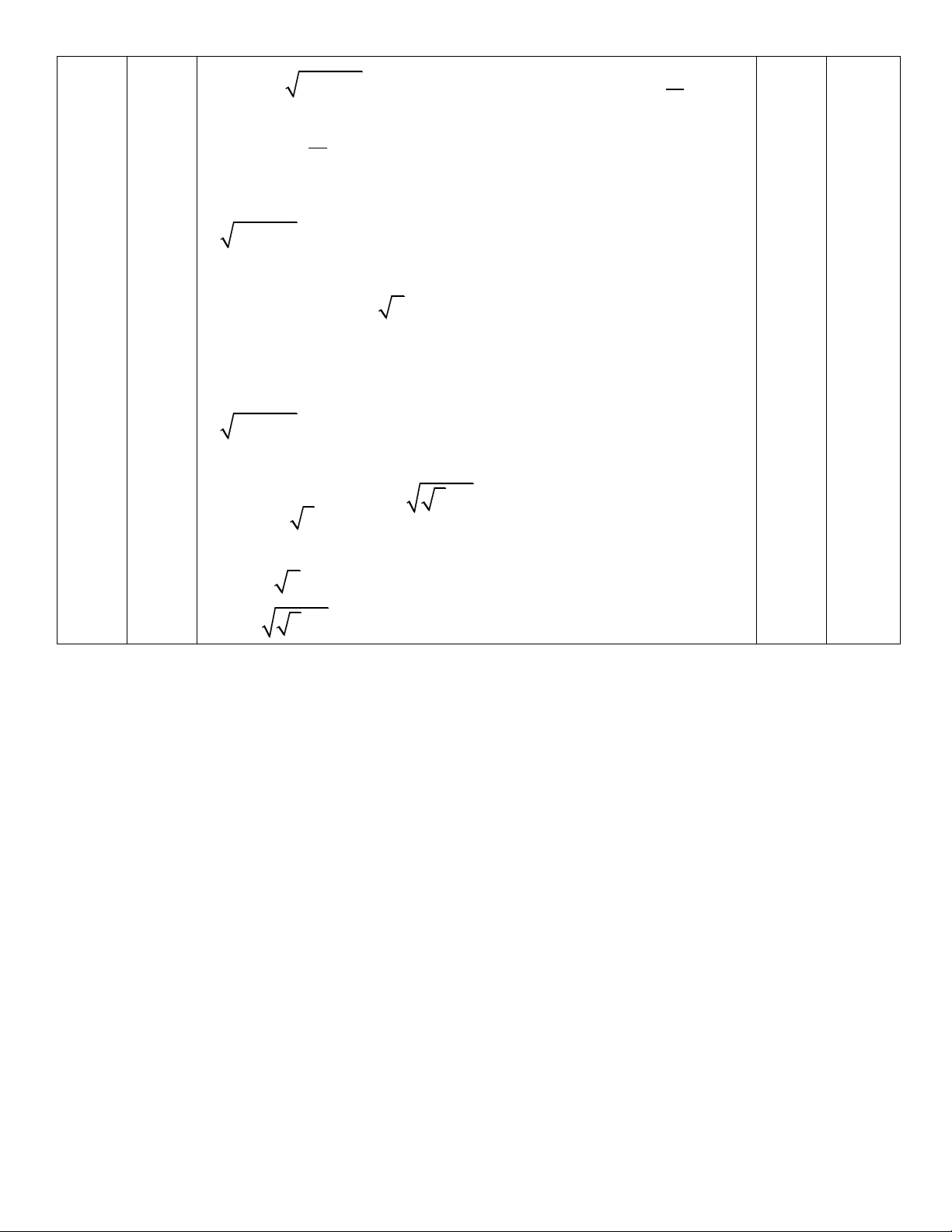
Đặt
2
2 2 4 2 2 2
2 4 2( 2 ) ( 2) 2
t
t x x t x x x x
Ta đƣợ pt
224
4 2 8 0 2
2
t
tt t t t
Với t -4 ta có:
2
4 2 4 2
2
00
2 4 4 2( 2 ) 16 2 8 0
02.
2
xx
xx x x x x
xx
x
Với t 2
2
4 2 4 2
2
00
2 4 2 2( 2 ) 4 2 2 0
03 1.
31
xx
xx x x x x
xx
x
Kết luận nghiệm ủa pt là
2.
31
x
x
0,25
0.25
0.25
0.25
1.0
Lưu ý: - Học sinh làm cách khác nếu đúng vẫn cho điểm tối đa.
- Học sinh không vẽ hình hoặc vẽ hình sai thì không chấm bài hình.













![Dàn ý và bài văn mẫu nghị luận xã hội ôn thi vào lớp 10: Tài liệu [mô tả/định tính]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250824/levanphuong15081979@gmail.com/135x160/23851756089220.jpg)












