TR NG Đ I H C BÁCH KHOA HÀ N IƯỜ Ạ Ọ Ộ
***VI N C KHÍ***Ệ Ơ
Đ ÁN THI T K C KHÍỒ Ế Ế Ơ
Đ TÀI: THI T K ROBOTỀ Ế Ế
Mã h c ph n : ME4099ọ ầ
H tên sinh viên : Vũ Công Đ nhọ ị
MSSV : 20100190
L p : K thu t C Đi n T 2 – K55ớ ỹ ậ ơ ệ ử
GVHD : PGS.TS.Phan Bùi Khôi
M C L CỤ Ụ
CH NG II: Thi t k mô hình 3DƯƠ ế ế
CH NG III: Tính toán đ ng h c robotƯƠ ộ ọ
CH NG IV: Tính toán đ ng l c h c robotƯƠ ộ ự ọ
CH NG V: Tính ch n đ ng c , t s truy n và thi t k h p gi mƯƠ ọ ộ ơ ỷ ố ề ế ế ộ ả
t cố
GVHD: PGS.TS.PHAN BÙI KHÔI 2
L I NÓI Đ UỜ Ầ
GVHD: PGS.TS.PHAN BÙI KHÔI 3
CH NG I: C s tính toánƯƠ ơ ở
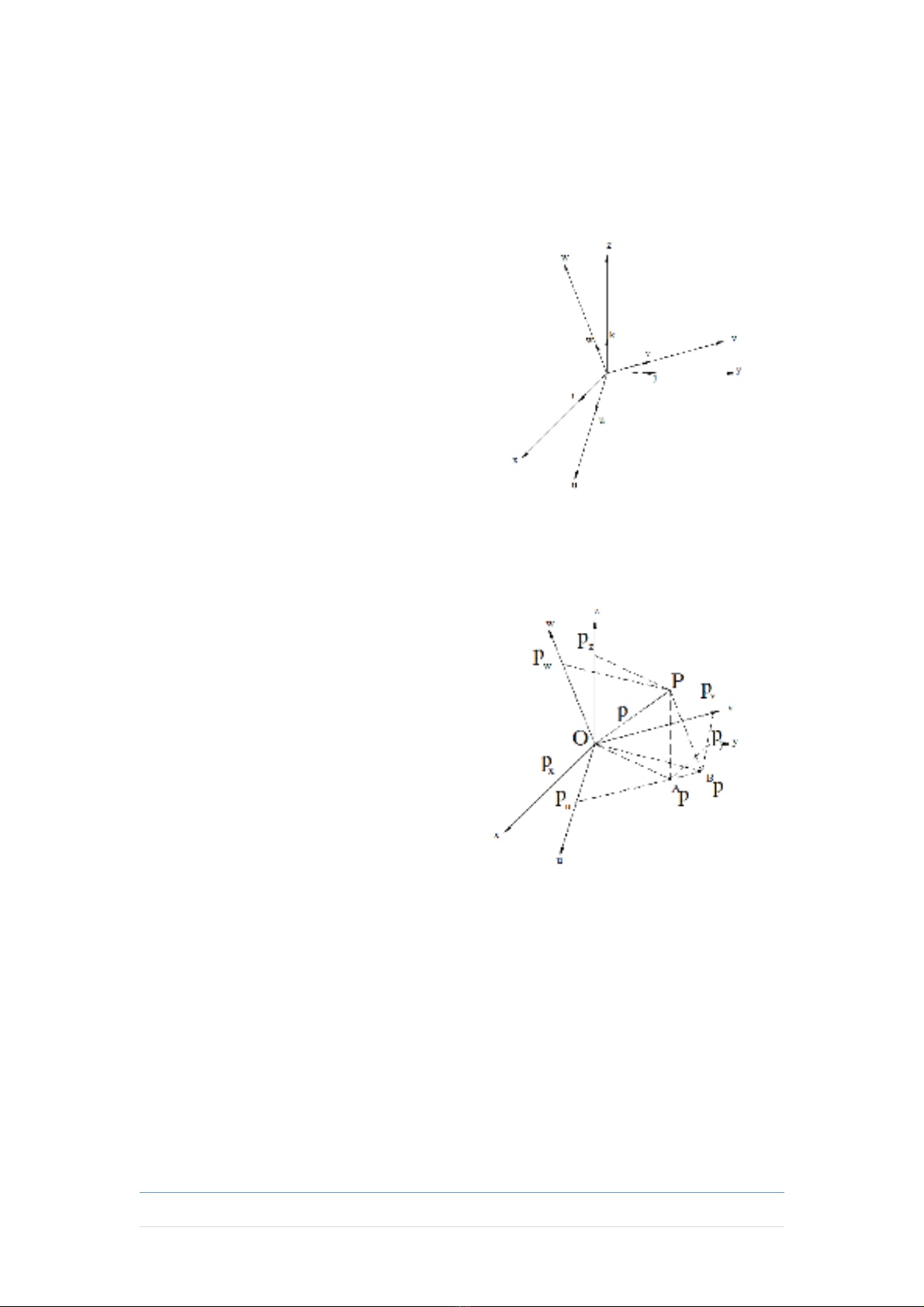
1.1. Ma tr n cosin ch h ng và ma tr n quay c a v t r nậ ỉ ướ ậ ủ ậ ắ
1.1.1. Ma tr n cosin ch h ngậ ỉ ướ
- Đ nh nghĩa: Cho 2 h quy chi uị ệ ế
chung gôc O:
+ H Oxyz c đ nhệ ố ị
+ H Ouvw đ ngệ ộ
Khi đó ma tr n cosin ch h ng c aậ ỉ ướ ủ
h quy chi u B đ i v i h quy chi uệ ế ố ớ ệ ế
A đ nh nghĩa nh sau:ị ư
Trong đó là 3 véc t đ n v trong h quy chi u c đ nh Aơ ơ ị ệ ế ố ị
là 3 véc t đ n v trong h quy chi u đ ng Bơ ơ ị ệ ế ộ
- P là m t đi m trong không gian. Ta có bi u di n c a P trong A, B:ộ ể ể ễ ủ
D dàng nh n th yễ ậ ấ :
Hay Ap = ARB Bp
GVHD: PGS.TS.PHAN BÙI KHÔI 4
* Nh n xétậ : Ma tr n cosin ch h ng mô t h ng c a h quyậ ỉ ướ ả ướ ủ ệ
chi u B đ i v i h quy chi u A. Nó bi n đ i t a đ c a đi m Pế ố ớ ệ ế ế ổ ọ ộ ủ ể
tùy ý trong h quy chi u đ ng B sang t a đ c a nó trong h quyệ ế ộ ọ ộ ủ ệ
chi u c đ nh Aế ố ị
1.1.2. Ma tr n quayậ
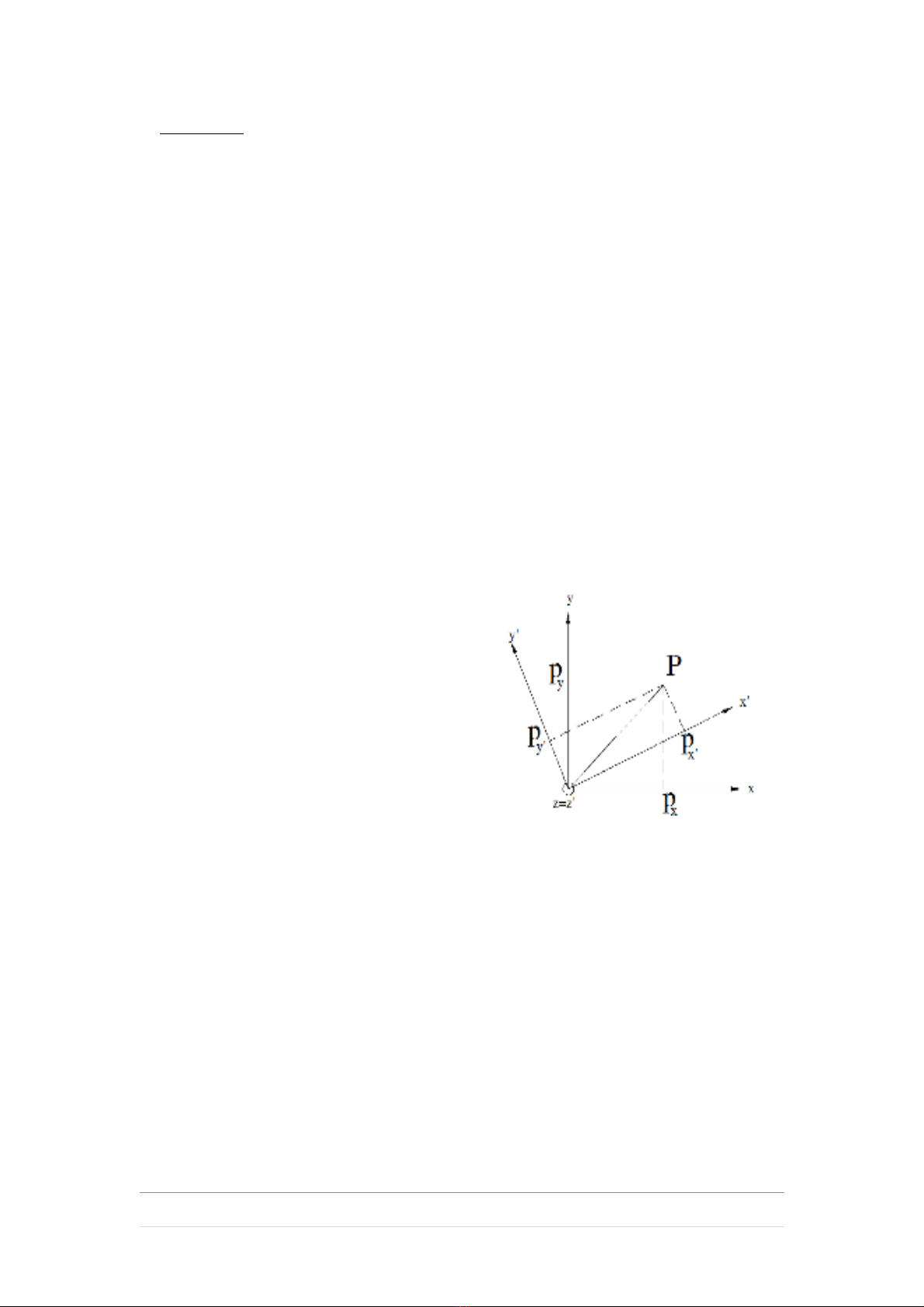
- Xét hai h quy chi u chung g c O liên h v i nhau b i phép quayệ ế ố ệ ớ ớ
m t góc quanh tr c z. G i p, p’ là vecto t a đ đi m P trong h Oxyzộ ụ ọ ọ ộ ể ệ
và Ox’y’z’. Ta có :
là ma tr n cosin ch h ngậ ỉ ướ
- Ma tr n cosin ch h ng Rậ ỉ ướ z bi u di n h ng c a m t h quyể ễ ướ ủ ộ ệ
chi u đ i v i h quy chi u khác, cũng chính là bi u di n phép quayế ố ớ ệ ế ể ễ
m t h quy chi u. Vì v y thông th ng ng i ta g i ma tr n cosin chộ ệ ế ậ ườ ườ ọ ậ ỉ
h ng là ma tr n quay.ướ ậ
- Các ma tr n quay c b nậ ơ ả (gi thi t các góc quay d ng)ả ế ươ :
+ Phép quay 1 góc quay tr c xụ0 :
+ Phép quay 1 góc quay tr c yụ0 :
+ Phép quay 1 góc quay tr c zụ0 :
1.2. Đ nh v , h ng và v trí c a v t r nị ị ướ ị ủ ậ ắ
GVHD: PGS.TS.PHAN BÙI KHÔI 5