1
Formal Specification of Agent Behaviour through
Environment Scenarios
Hong Zhu
School of Computing and Mathematical Sciences, Oxford Brookes University
Gipsy Lane, Headington, Oxford, OX3 0BP, England
hzhu@brookes.ac.uk, Tel:++44 1865 483670, Fax:483666
Abstract. Scenarios are typical situations that may occur in the operation of a
software system. Scenario analysis plays an important role in software
requirements analysis and design. This paper introduces a formal notation for
the specification of scenarios in agent-based systems. The autonomous and
collaborative behavior of an agent can be formally specified by a set of rules
describing its activity in various scenarios. The power of the approach is
illustrated by the formal specification of Maes' personal assistant agent
Maxims. The paper also shows that agents' social behavior, such as speech act,
can also be formally specified as scenario-reaction rules.
1 Introduction
Being autonomous, proactive and adaptive, an agent-based system may demonstrate
emergent behaviours, which are neither designed nor expected by the developers or
users of the system. Whether or not such emergent behaviours are advantageous,
methods for the specification of agent behaviours should be developed to enable
software engineers to analyse the behaviour of agent-based systems. The past few
years have seen a rapid growth in the research on formal models of agent-based
systems specified in various formalisms and logics, such as temporal logics, first
order logics, and game theories, etc., see e.g. [1, 2, 3]. However, there are few
researches on the language facilities and features that support the formal specification
and verification of agent-based systems, although efforts have been made to define
new formal specification languages, for example, LW [4], DESIRE [5] and ETL [6].
This paper reports our research in progress on a formal method for the
specification, proof and analysis of the behavior of agent-based systems. The basic
idea is to specify an agent's behaviour by a set of rules that govern its reactions to
various scenarios in its environment. A formal specification language, called SLAB,
is being designed to facilitate such formal specifications and analysis of multi-agent
systems. Instead of giving a complete definition of the language, this paper presents
the language facilities that we identified and the rationale behind the design decisions.
We also illustrate by examples the use of the facilities in the specification of
autonomous and collaborative behaviors of multi-agent systems.
2
2 SLAB – A Formal Specification Language of Agent Behaviour
It is widely recognised that formal methods are difficult to scale up. Modularity and
composibility are among the solutions to this problem advanced in the literature. The
question is then what are the 'modules' in a formal specification of an agent-based
system and how to compose them together into a system. In search for an answer to
these questions, we turned to more fundamental questions like what is the essence of
agent-based comp uting and what makes agents an appealing and powerful approach.
As Jennings pointed out [7], such questions can be tackled from many different
perspectives ranging from the philosophical to the pragmatic. In the design of the
SLAB language, we have taken a pragmatic approach in order to obtain a practical
solution. We are concerned with the language facilities that support the specification
and reasoning of agent-based systems from a software engineering point of view. In
this section, we discuss how such a view led to our design decisions.
2.1 Agents as Encapsulations of Behaviour
Of course, agent is the most basic concept of agent-oriented or agent-based
computing. Although there is much debate about exactly what constitute agenthood,
we believe that Jennings' definition represents a common view from many
researchers. It reads 'an agent is an encapsulated computer system that is situated in
some environment, and that is capable of flexible, autonomous action in that
environment in order to meet its design objectives' [7]. According to this definition,
an agent is an entity that observes its environment and takes its action (or reaction)
according to its internal state, which can be driven by its believe, desire and intention
and to follow a plan to achieve a specific goal. Thus, agents are active and persistent.
They execute concurrently and autonomously.
Therefore, an agent has a set of variables represents its internal state and a set of
actions it can take. Being an active entity, an agent's internal state is persistent in the
sense that there is always a value bound to the variables. In contrast, actions are
temporal in the sense that it is possible that no action is taken at a particular time.
Another difference between state variables and actions is that state variables can vary
continuously as time changes. In other words, a state variable can be a function of
time. To communicate with the outside world, an agent must have some actions that
are observable by other agents, and be able to show its state to the outside world. For
example, Maes' Maxims agents have facial expressions to communicate with the
users. However, an agent also needs to be able to hide some of its internal state and
actions. The state variables and actions are, therefore, divided into two types, those
visible from the outside and those internal and invisible from the outside.
The most important feature that distinct agents from objects in the object-oriented
paradigm is the so-called autonomous behaviour. Although an object also has internal
states and a set of actions (which are called methods in object-oriented terminology),
it has no control over whether and when to take an action. A method must be executed
when a message is received. In contrast, an agent can decide whether or not and when
to take an action when a message is received or a certain event happens in the
environment. Its capability of controlling over its internal state and action is the
3
characteristics of autonomous behaviour. In other words, an agent's behaviour is
determined by its design rather than by the environment. In this sense, we say that an
agent is an encapsulation of states, action and behaviour, or shortly, an encapsulation
of behaviour.
We believe that the power of agent-oriented approach comes from the
encapsulation of behaviour, which enable an agent to achieve its design objectives in
dynamic and unknown environment by controlling its behavior and adapting its
behavior according to the environment, rather than controlled by the environment.
Therefore, in the design of an agent, the complexity of the problem due to the
dynamic nature and unknown characteristics of the environment can be reduced to the
minimum. This understanding of the concept of agent led us to the first design
decision in the development of the formal specification language SLAB. That is, the
basic building block in an agent-oriented specification language should be agent,
which encapsulates four interrelated parts: (1) the specification of state space, (2) the
specification of actions, (3) the specification of behaviour, and (4) the specification of
the part of environment that it observes.
The following gives SLAB's syntax in EBNF of specifications of agents. It can also
be equivalently represented in a graphic form similar to the schema in Z [8].
agent-description ::= ::=
agent name [: { class-name,}] {instantiation}*;
[ environment-description; ]
[ structure-description; ]
[ behavior-description ]
end name
structure-description ::=::=
[ Var {[ * ] identifier: type; }+ ] [Action {action}+]
action ::=::= [*] identifier; | identifier ({ [parameter:] type,}+)
In SLAB, the state space of an agent is described by a set of variables with keyword
VAR. The set of actions is described by a set of identifiers with keyword ACTION.
An action can have a number of parameters. An asterisk before the identifier indicates
invisible variables and actions.
The power of agent-based system can be best demonstrated in a dynamic
environment [9, 10] because an agent can adapt its behaviour into the environment to
achieve its designed purpose. Therefore, the specification of an agent-based system
must also specify how the environment affects the behaviour of the agent. To do so,
we must first answer the question what is the environment of an agent. A simple
answer to this question is that in a multi-agent system, the environment of an agent
consists of a number of agents and a number of objects. However, having defined
agents as encapsulations of behaviours, we regard object as a degenerated form of
agent. The behaviour of an object is simply to respond to every message sent to the
object by executing the corresponding method. Based on this understanding of the
relationship, our second design decision is to specify a multi-agent system as a set of
agents, nothing but agents.
System ::= {Agent-description | class-description}*
The environment of an agent is a subset of the agents in the system that may influence
its behaviour. The syntax for the description of environments is given below.
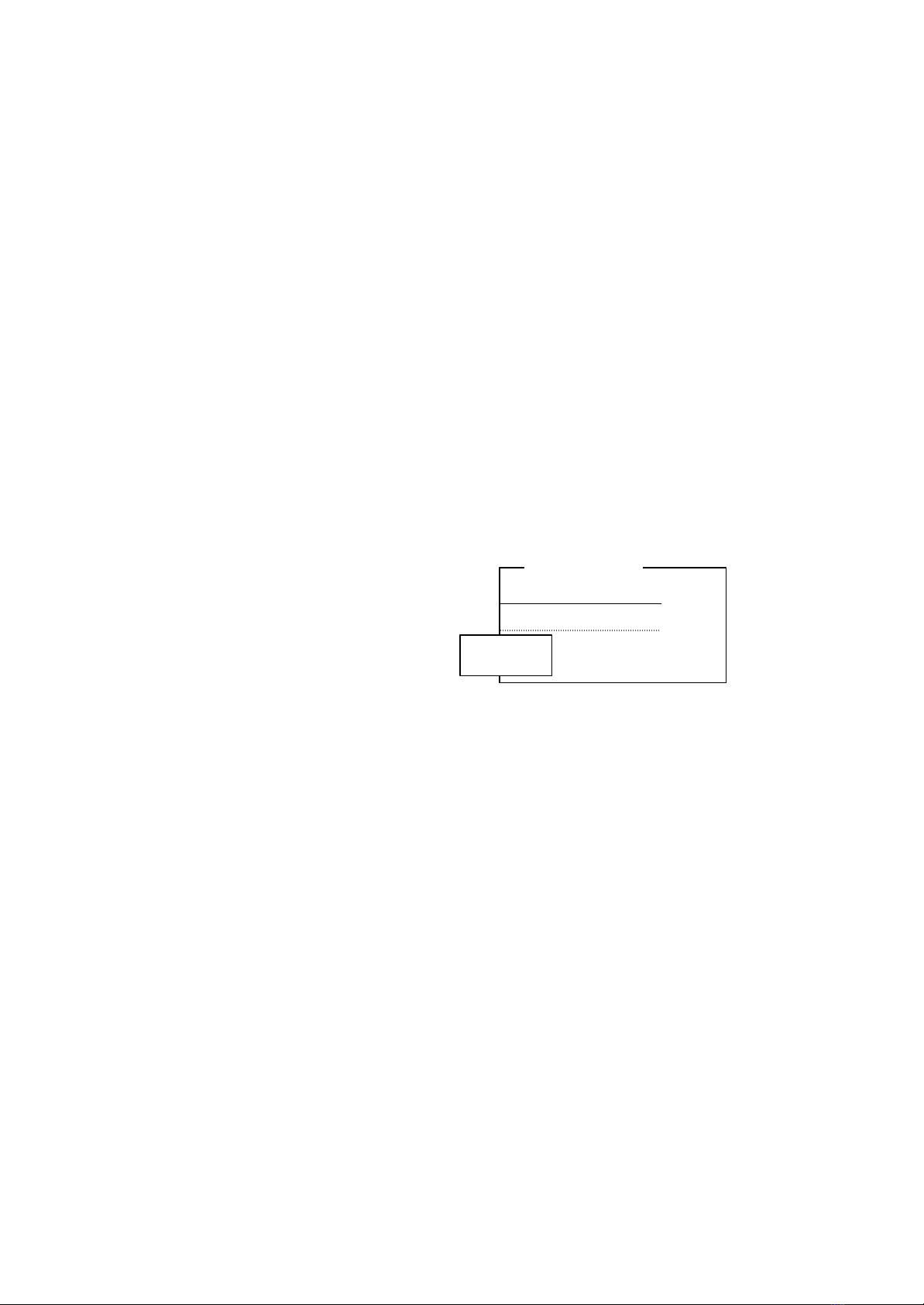
Environment-description ::= { name | All: class-name | variable : class-name }*,
Visible state-variables and actions
Invisible state-variables and actions
Behaviour-specification
Name: Classes
Environment
description
4
where a name indicates a specific agent in the system. 'All' means that all the agents
of the class have influence on its behavior. A variable is a parameter in class
specification. When instantiated, it indicates an agent in the class.
2.2 Classes of Agents as Birds of a Feather
In object-oriented languages, a class is considered as the set of objects of common
structure and function. Similarly, a class in SLAB is considered as a set of agents of
same structural and behavioral characteristics. If an agent is specified as an instance
of a class, it inherits the structure and behaviour descriptions from the class.
However, in addition to those inherited structure and behaviour, an agent can also
have additional behaviour and structure descriptions of its own. The syntax and
graphic representation of class specification is given below.
class-description ::=::=
class name [ <= {class-name} ]
{instantiation};
[ environment-description;]
[ structure-description; ]
[ behavior-description; ]
end name
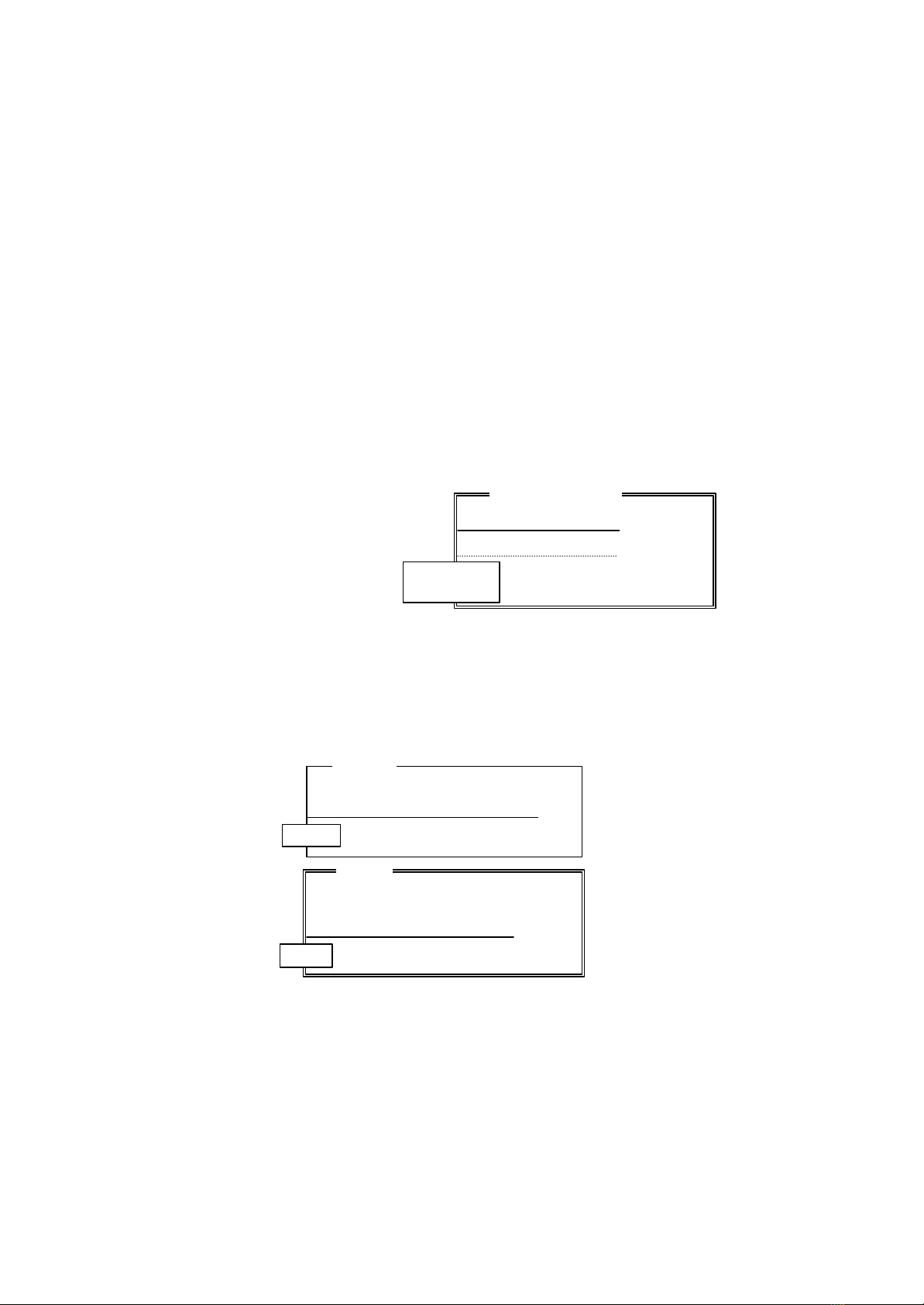
For example, consider a system of mice in a maze. The maze consists of 10 by 10
squares. Each square can either be occupied by a rock or has a bean, or be empty. A
mouse can move from one square to its adjacent square if the square is not occupied
by a rock. It can pick up a bean if the square has a bean. The structure of the system
can be specified by a class Mice and an agent Maze as below. The agent Maze
represents the maze. It can be understood as the manager of the maze to up date the
state of the maze when a mouse in the system picks up a bean. The specification of
the dynamic behaviour will be given later.
As a template of agents, a class may have parameters. The variables specified in the
form of “identifier: class-name” in the environment description are parameters. Such an
identifier can be used as an agent name in the behaviour description of the class.
When class name(s) are given in an agent specification, the agent is an instance of the
Visible state-variables and actions
Invisible state-variables and actions
Behaviour-specification
Name <= Classes
Environment
description
VAR Bean: {1,..,10} × {1,..10} → Boolean
Rock: {1,..,10} × {1,..10} → Boolean
Behavior-description
All: Mice
Maze
VAR Position: {1,..,10} × {1,..10}
ACTION Pick-bean ({1,..,10}, {1,..10})
Move ({West, east, south, north})
Behaviour-description
Maze
Mice
5
classes. The instantiation clause gives the details about how the parameters are
instantiated.
A class can also be defined as a subclass of existing classes by indicating the
super-classes. A subclass inherits the structure and behaviour descriptions from its
super-classes. It may also have some additional actions and obey some additional
behaviour rules if they are specified in the subclass declaration. Some of the
parameters of the super-class may also be instantiated in a subclass. As shown in
section 3.2, the class and inheritance facilities provide a powerful vehicle to describe
the normality of a society of agents. Multiple inheritances are allowed in the SLAB
language to allow an agent to belong to more than one society and play more than one
role in the system at the same time.
2.3 Scenarios as Patterns of Behaviours
The notion of scenario has been used in a number of areas in computing with different
meanings. For example, in UML, scenarios are described as the sequences of
messages passing between the system and the objects that represent the users. In the
application of scenarios in testing software requirements [11], a scenario is described
as an activity list that represents a task of human computer interaction. Generally
speaking, a scenario is a set of situations that might occur in the operation of a system
[12]. No matter how scenarios are described, its most fundamental characteristic is to
put events in the context of the history of behaviour. Here, in a multi-agent system,
we consider a scenario as a set of typical combinations of the behaviours of related
agents in the system.
The use of scenarios and use cases in requirements analysis and specification has
been an important part of object-oriented analysis, see for example, [13]. However,
because an object must respond in a uniform way to all messages that call a method,
there is a huge gap between scenarios and requirements models. The object-oriented
paradigm is lack of a method to analyse the consistency between use cases (or
scenarios) and requirements models and a method to synthesise requirements models
from use cases or scenarios, although such methods exist for structured analysis [12].
As extensions to OO methodology, the use of scenarios in agent oriented analysis and
design has been proposed by a number of researchers, for example [14, 15, 16]. In the
design of SLAB, we recognised that scenarios can be more directly used to describe
agent behaviour. The gap between scenarios and requirements models no longer
exists in agent-based systems because the agent itself controls the its behaviour. Its
responses can be different from scenario to scenario rather than be uniform to all
messages that call a method.
In SLAB, a basic form of scenario description is a set of patterns. Each pattern
describes the behaviour of an agent in the environment by a sequence of observable
state changes and observable actions. A pattern is written in the form of [p1, p2, ..., pn]
where n≥0. Table 1 gives the meanings of the patterns.
pattern ::=::= [ { event || [ constraint ] } ]
event ::= [ time-stamp: ] [ action ] [ ! state-assertion ]
action ::= ::= atomic-pattern [ ^ arithmetic-expression ]
atomic-pattern ::=::= $ | ~ | action-variable | action-identifier [ ( { arithmetic-expression } ) ]