112
HÌNH HOÏC
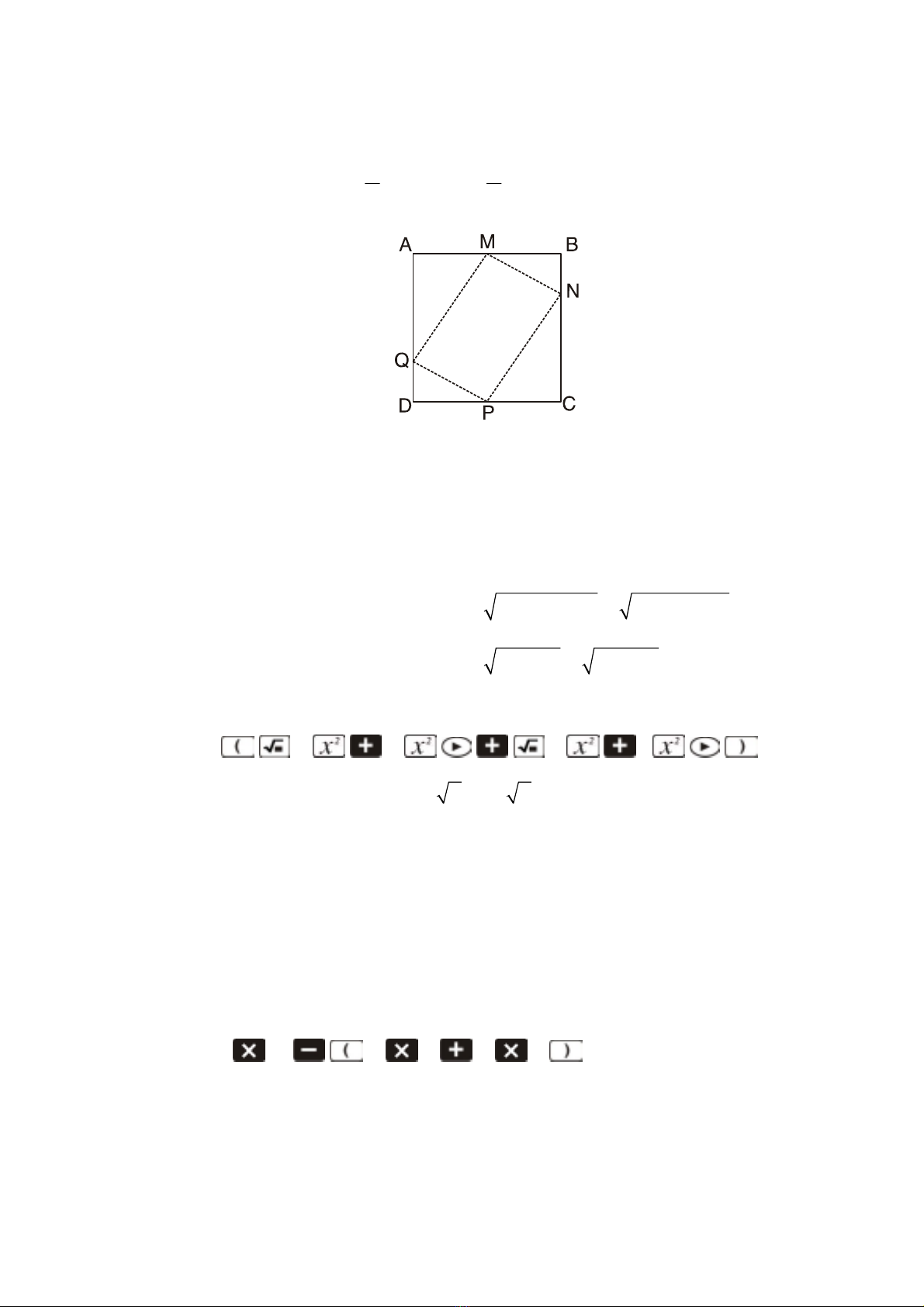
Ví duï: Cho hình vuoâng ABCD caïnh baèng 12. M, P laàn löôït laø trung
ñieåm AB, CD, BN = 1
4BC, QD = 1
4AD. Haõy tính chu vi vaø dieän tích
MNPQ.
Giaûi
MN, NP, PQ , QM , laàn löôït laø caïnh huyeàn cuûa caùc tam giaùc MBN,
NCP, PDQ, QAM. AÙp duïng ñònh lyù Pitago, tacoù :
Chu vi MNPQ laø : chu vi = 2 (QM +MN)
= 2( 22 22
AM AQ BM BN
)
= 2( 22 22
69 63 )
AÁn 2 6 9 6 3
Keát quaû: Chu vi MNPQ = 6 6 + 6 5 = 35,0497
Tính dieän tích :
Ta coù : S MNPQ = S ABCD – 2
AMQ QDP
(S S )
= ABAD – (AM
AQ + QD
DP)
= 1212 – (9
6 + 3
6)
AÁn 12 12 9 6 3 6
Keát quaû: Dieän tích S MNPQ = 72.
113
LÔÙP 9
ÑAÏI SOÁ
I. CAÊN BAÄC HAI, CAÊN BAÄC BA
1. Caên baäc hai
Ví duï 1: Soá naøo coù caên baäc hai laø
a) 3 ; b) 1,2
c) –0,2 ; d) – 8
Giaûi
Soá coù caên baäc hai laø:
a) 3 töùc soá ñoù laø 2
(3).AÁn 3 Keát quaû: 3
b) 1,2 töùc soá ñoù laø 1,2 2.AÁn 1.2 Keát quaû: 1 11
25 = 36
25 = 1,44.
c) –0,2 töùc soá ñoù laø (–0,2) 2.AÁn 0.2
Keát quaû: 1
25 .
d) – 8 töùc soá ñoù laø (– 8)2.AÁn 8
Keát quaû: 8
Ví duï 2: Tính caên baäc hai soá hoïc cuûa:
a) 1,21 ; b) 1,44 ;
c) 1,69 ; d) 1,96 ;
Giaûi:
AÁn 1.21 . Keát quaû: 11
10 AÁn tieáp ñöôïc 1,1.
AÁn 1.44 . Keát quaû: 6
5 AÁn tieáp ñöôïc 1,2.
AÁn 1.69 . Keát quaû: 13
10 AÁn tieáp ñöôïc 1,3.
AÁn 1.96 . Keát quaû: 7
5 AÁn tieáp ñöôïc 1,4.
2. Caên baäc ba
Ví duï 1: Tìm x bieát:
a) 3x = 1,7 b)
3(x 3) = 18
Giaûi
a) Ta coù 3x = 1,7 hay x = 1,7 3. AÁn 1.7 Keát quaû: 4913
1000
tieáp ñöôïc 4,913.
114
b) Ta coù 3(x 3) = 18 hay x = 18 3 + 3. AÁn 18 3
Keát quaû: 5835
Ví duï 2: Tính caên baäc ba cuûa
a) 1331 ; b) 1728 ;
c) 2197 ; d) 2744 ;
Giaûi
AÁn ( )1331 . Keát quaû: 31331 = 11.
AÁn ( )1728 . Keát quaû: 31728 = 12.
AÁn ( )2197 . Keát quaû: 32197 = 13.
AÁn ( )2744 . Keát quaû: 32744 = 14.
*3. Luyõ thöøa-caên soá baát kì.
Ví duï 1: Tính
a) 210 AÁn 2 10 Keát quaû: 1024.
b) (–3) 5 AÁn 3 5 Keát quaû: –243.
c)
4
2
3


 AÁn 2 3 4 Keát quaû: 16
81
d) 4 3 AÁn 4 3 Keát quaû: 4 3
= 3
1
4 = 1
64 = 0,015625.
Ví duï 2: Tính
a) 483521 b)
532768
c) 7128 d)
10 1024
Giaûi
AÁn ( ) 4 83521 . Keát quaû: 17.
AÁn ( ) 5 32768 . Keát quaû: 8.
AÁn ( ) 7 128 . Keát quaû: 2.
AÁn ( )10 1024 . Keát quaû: 2.
Baøi taäp thöïc haønh
1. Tính
a) 310 ÑS: 59049 b)
7
1
2



ÑS: – 1
128
c) (–7) 4 ÑS: 2401 d) 1,12 3 ÑS: 1,404928
e) 5 1 ÑS:
1
5 f) 3
4
ÑS: 1
81
115
2. Tính
a) 1849 ÑS: 43
b) 2683,24 ÑS:
259
5 = 51,8
c) 729
1849 ÑS:
27
43
d) 128 2
ÑS: 16.
e) 25281
3 867 ÑS:
53
17
3. Tính
a) 3117649 ÑS: 49 b) 30,032768 ÑS: –0,32
c) 420736 ÑS: 12 d)
72187 ÑS: –3
e) 9262144 ÑS: 4 f)
5371293
16807 ÑS:
13
7
4. Tính giaù trò cuûa bieåu thöùc coù chöùa caên
B = 3 1
8x2 + 1
16 x3 – 223
5(6x 1) (x 9) taïi x = 4
AÁn 4 (STO) (X) ( Gaùn 4 cho X )
AÁn tieáp 3 ( )1 8 (X) 1 16
(X) 5 ( ) 6 (X) 1
(X) 9 .
Keát quaû: B = 29.
Baøi taäp thöïc haønh
a) A = 2
3(4x 1)(3x 5) – (x 2 + 2x + 3) taïi x = 4. ÑS: –10
b) B = 3
x10
2x 3
– 3
4x 1
x11
taïi x = 3. ÑS: 1289
342
c) C = 2
x1 x6 – 2
1
5(x 5) x 4x 4

taïi x = 10.
ÑS:
27
119
d) D = 32
3x 7 4 7x
x6x

taïi x = – 1
2 ÑS: –2,1786
116
II. HAØM SOÁ BAÄC NHAÁT
Ñieàn caùc giaù trò cuûa haøm soá y = –3x + 2 vaøo baûng sau:
x –5.3 –4 –4
3 2.17 43
7 57
y
Giaûi
Ghi vaøo maøn hình –3(–5.3) + 2 baèng caùch aán 3 5.3
2 vaø aán KQ: 179
10 = 17.9
AÁn vaø chænh laïi thaønh –3(–4 )+ 2 vaø aán KQ: 14.
AÁn vaø chænh laïi thaønh –3 4
3



+ 2 vaø aán KQ: 6
AÁn vaø chænh laïi thaønh –3(2.17) + 2 vaø aán KQ: – 451
100 = –4.51
AÁn vaø chænh laïi thaønh –3 3
47



+ 2 vaø aán KQ: – 79
7
AÁn vaø chænh laïi thaønh –3(5 7) + 2 vaø aán
KQ: 2 – 15 7 = –37.6863
Ta ñöôïc baûng keát quaû
x –5.3 –4 –4
3 2.17 43
7 57
y 17.9 14 6 –4.51 79
7 –37.686
Ví duï 2: Ñieàn caùc giaù trò cuûa haøm soá y = 3x 2vaøo baûng sau:
x –5.3 –4 –4
3 2,17 43
7 57
y
Giaûi
Laøm töông töï nhö ví duï 1, ta ñöôïc keát quaû
x –5.3 –4
–4
3 2,17 43
7 57
y 84.27 48 16
3 14.1267 2883
49 525