
Giải tích 2 – Đề số 17
Câu 1: Cho
2
3
( , ) ln 3
f x y y x y
. Tìm
(0,0), (0,0)
f f
x y
.
Bài giải
0 0
0 0
,0 0,0 ln 3 ln 3
lim lim 0 (0,0) 0
0, 0,0 ln 3 ln 3
lim lim 1 (0,0) 1
x x
y y
f x f f
x x x
f y f y f
y y y
Câu 2: Tìm cực trị có điều kiện: 3 3
( , ) ; 16
xy
f x y e x y
.
Bài giải
Xét:
3 3
' 2
4
' 2
3 3
,
3 0
3 0 2( )
6
16
xy
xy
x
xy
x
L x y e x y
L ye x
e
L xe y x y
x y
Vậy có một điểm dừng là: P(2,2)
'' 2
4
'' 2
4
''
6
2
65
1
xy
xx
xy
yy
xy
xy
L y e x
A C e
L x e y B e
L xy e
2 2 2 4
2 2 10
d L P dx dy dxdy e
Lấy vi phân 2 vế tại P của phương trình 3 3
16
x y
:
12 12 0
dx dy dy dx
Thế vào trên ta được:
2 2
6 0
d L P dx
Vậy P là điểm cực đại.
Câu 3: . Tính tổng
1
( 1)
2 4 6 (2 )
n
n
n
Bài giải

Ta có:
1 1 1 1
1
2
1
1 1 0
1
2
1
( 1) ( 1) 1
2 4 6 (2 )
2 . ! 2 . ! 2 . !
1
1 1 1 1
2
2 2 ! 2
2 . ! 2 . 1 !
11
2 . !
1
1
2
n n n
n n n n
n
n n
n n n
n
n
n n n
Sn
n n n
ne
n
n n
e
n
S e
Câu 4: Sử dụng khai triển Maclaurint của hàm dưới dấu tích phân thành chuỗi, tính
0
1
x
xdx
e
Bài giải
Câu này đạo hàm được nhưng rất khó và sau khi lấy tích phân vẫn không tính tổng lai
được.
Có phương pháp sau không phải là khai triển maclaurint, ý tương hay nhưng vẫn không
giải quyết bài này được, các em tham khảo nhé:
1
0 0
1
2
0 0
0 0
1 1
1 1
1
1
11
xn n
n x
x nx
x x n n
n
nn x
xn n
x xe xe e xe
e e
xdx xe dx
en
Tới đây ta lại gặp vấn đề về tính tổng. Bài này Thầy nghĩ không tính được.
Câu 5:
Tính tích phân
2 2
0
2sign
x y dxdy
với D
0 3,0 3
x y
.
Bài giải
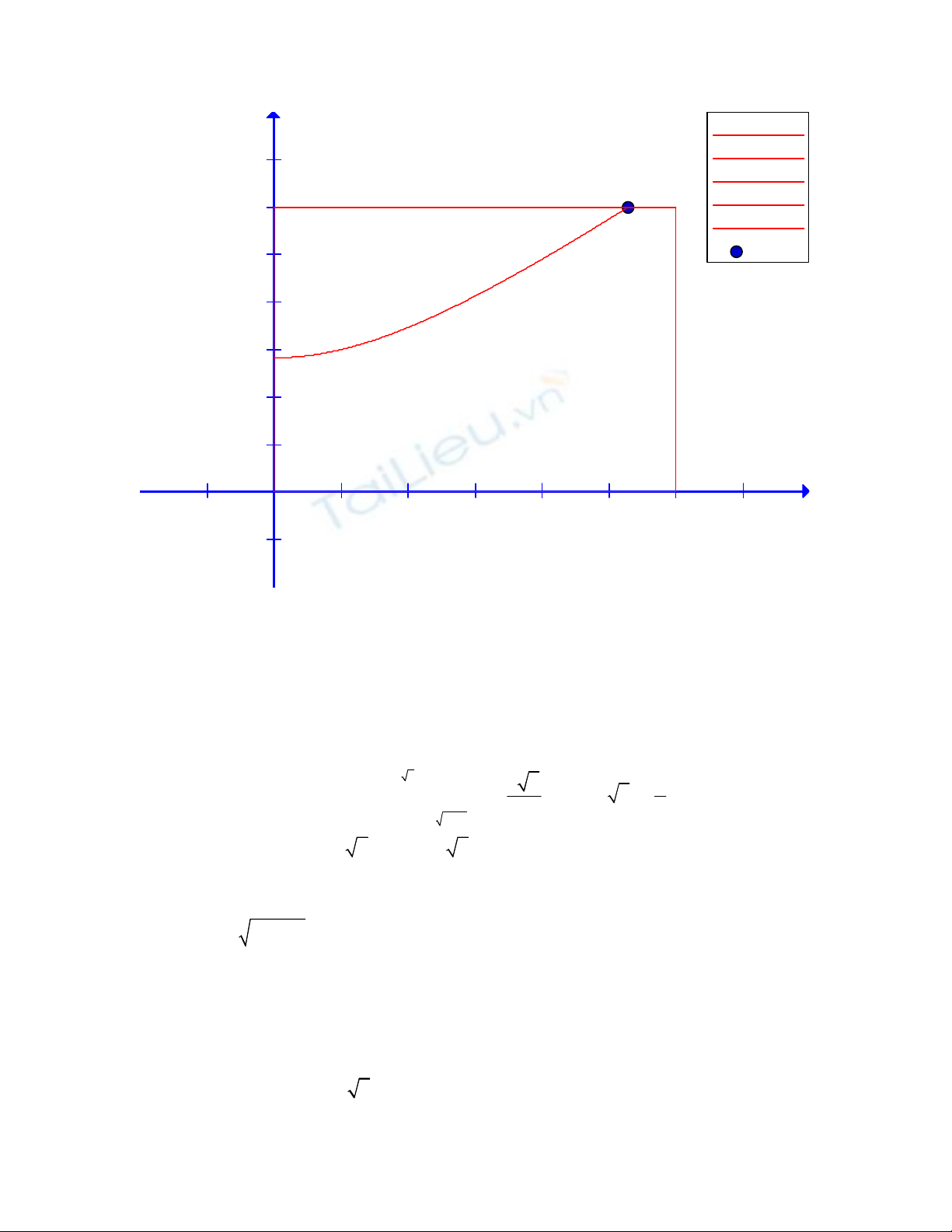
f(x)=0
f(x)=3
x(t)=0 , y(t)=t
x(t)=3 , y(t)=t
f(x)=sqrt(x^2+2)
Series 1
-0.5 0.5 1 1.5 2 2.5 3 3.5
-0.5
0.5
1
1.5
2
2.5
3
3.5
x
y
D1
D2
A
Trên
2 2 2 2
1
2 2 2 2
1
: 2 0 ( 2) 1
: 2 0 ( 2) 1
D x y sign x y
D x y sign x y
1 2
1 2 2
1 1 ( ) ( ) 2 ( )
D D D
dxdy dxdy dt D dt D dt D dt D
Với D=9
Và
2
2
7 3
2
02
3 7 1
( ) ln 3 7 ln 2
2 2
9 3 7 2ln 3 7 ln 2
Dx
dt D dxdy dx dy
y
Câu 6: Tính tích phân đường
2 2 2
C
I y z dx z x dy x y dz
, với C là giao
của mặt nón 22
y z x
và mặt cầu 2 2
4
2
x y z
ngược chiều kim đồng hồ theo
hướng trục Ox.
Bài giải
Nhận xét : mặt nón và mặt cầu cắt nhau theo một đường tròn nằm trong mp x=4
Gọi S là mặt trước của hình tròn có biên là C
2 2 2
4
:2
x y z
Sx

Áp dụng công thức Stoke
2 2 2
(1 2 ) (1 2 ) (1 2 ) (1 2 )
C
S S
I y z dx z x dy x y dz
z dydz x dxdz y dydx z dydz
(vì trên S (x=4): dx=0)
2 2
0 0
(1 2 sin ) 2
d r rdr
Câu 7: Tính tích phân mặt loại hai 3 3 3
S
I x dydz y dzdx z dxdy
, với S là mặt trong
của vật thể giới hạn bởi
2 2 2 2 2
1 4,
x y z y x z
.
Bài giải
Dùng O-G:
2 2 2
3
V
I x y z dxdydz
Đổi sang toạ độ cầu mở rộng:
0
sin cos
4
sin sin 0 2
os 1 2
z
x
y c
2 2
42 2
0 0 1
93
3. . .sin 2 2
5
I d d d


























