Bài giảng Giải tích B2: Giải tích vectơ

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:105

Thêm vào BST

Báo xấu

1
lượt xem 0
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Giải tích B2: Giải tích vectơ gồm có những nội dung chính sau: Trường vectơ, tích phân đường, định lý cơ bản của tích phân đường, định lý Green Curl và Divergence, mặt tham số và diện tích mặt, tích phân mặt, định lý Stocks, định lý Divergence. Mời các bạn cùng tham khảo để nắm bắt các nội dung chi tiết.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Giải tích B2: Giải tích vectơ

GIẢI TÍCH VECTƠ
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Trường vectơ vận tốc, biểu thị hướng và độ lớn của gió ở San Francisco Bay, 2:00, Feb, 21, 2007. GIẢI TÍCH B2 256/??
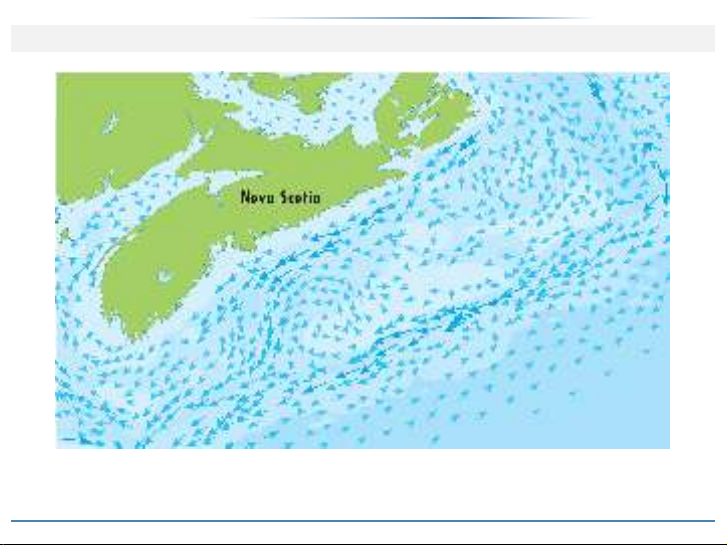
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Trường vectơ vận tốc, biểu thị các dòng hải lưu quanh bờ biển Nova Scotia. GIẢI TÍCH B2 257/??
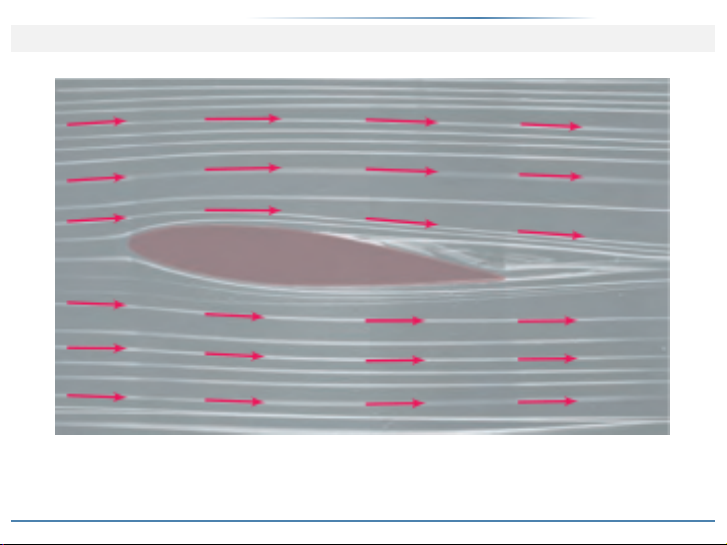
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Trường vectơ vận tốc, biểu thị các dòng khí thổi qua cánh máy bay ở thế nghiêng. GIẢI TÍCH B2 258/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Định nghĩa 1 D là một tập trong R2 (miền phẳng). Một trường vectơ trên D ! là một hàm vectơ F gán mỗi điểm .x; y / 2 D với một vectơ hai ! chiều F .x; y /. 2 E là một tập trong R3 . Một trường vectơ trên E là một hàm ! vectơ F gán mỗi điểm .x; y ; z/ 2 E với một vectơ 3 chiều ! F .x; y ; z/. GIẢI TÍCH B2 259/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Ví dụ ! ! ! Phác họa trường vectơ F .x; y / D y i Cx j. Giải. Ta lập bảng giá trị và vẽ vài vectơ GIẢI TÍCH B2 260/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Sau đây thêm vài ví dụ về trường vectơ: ! Trường ! F .x; y / D h y ; xi Trường F .x; y / D hy ; sin xi GIẢI TÍCH B2 261/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ ! Trường Trường F .x; y ; z/ D hy ; 2; xi F .x; y ; z/ D y ! C z! C z! ! i j x GIẢI TÍCH B2 262/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Trường hấp dẫn. Theo định luật hấp dẫn của Newton, cường độ lực hút ˇ!ˇ lẫn nhau giữa hai vật có khối lượng m và M là ˇ F ˇ D mMG =r 2 , trong đó G là hằng số hấp dẫn và r là khoảng cách giữa hai vật. Giả sử vật có khối lượng M đặt tại gốc tọa độ O trong R3 (ví dụ M là khối lượng trái đất và O là tâm trái đất), vectơ vị trí của vật có khối lượng x r m là ! D hx; y ; zi (các nhà Vật lý thường dùng ký hiệu ! thay cho !). x Lực hút tác động lên vật m hướng về tâm với vectơ đơn vị chỉ hướng là x x !=j!j. Do đó trường lực hấp dẫn là !! mMG ! F.x / D x x j!j3 !! mMGx ! mMGy ! F.x / D i j .x 2 Cy 2 C z 2 /3=2 .x 2 Cy 2 C z 2 /3=2 mMGz ! k .x 2 C y 2 C z 2 /3=2 GIẢI TÍCH B2 263/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Trường tĩnh điện. Tương tự trường hấp dẫn, ta có trường tĩnh điện xung quanh một điện tích Q được cho bởi công thức !! "Q E . x / D ˇ!ˇ3 ! ˇx ˇ x " là hằng số, tùy thuộc vào các đơn vị điện tích được dùng. Nếu Q dương Trường lực hấp dẫn. thì trường tĩnh điện hướng ra ngoài gốc tọa độ. GIẢI TÍCH B2 264/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ TRƯỜNG GRADIENT VÀ TRƯỜNG BẢO TOÀN 1 Một hàm số (còn gọi hàm vô hướng, scalar function) theo biến x x x ! D hx; y i hoặc ! D hx; y ; zi, sẽ cho một trường rf .!/, được gọi là trường gradient. ! 2 Một trường vectơ F được gọi là trường bảo toàn (conservative vector field) nếu nó là gradient của một hàm vô hướng f , nghĩa là tồn ! tại hàm số f sao cho F D rf . Khi đó f được gọi là hàm thế ! (potential function) của trường F . GIẢI TÍCH B2 265/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.1. Trường vectơ Ví dụ. Trường vectơ gradient của hàm số f .x; y / D x 2 y y 3 được vẽ chung với contour map của f như hình bên. Lưu ý các vectơ gradient có hướng vuông góc với các đường đồng mức. Ở những chỗ các đường đồng mức càng sát nhau, độ dốc theo hướng gradient càng lớn, do đó vectơ được vẽ càng dài. Ví dụ. Trường lực hấp dẫn !! F . x / D . mMG =ˇ!ˇ3 /! là một x x ˇ ˇ trường bảo toàn, vì nó là gradient Ghi chú. Không phải trường vectơ của hàm vô hướng nào cũng là trường bảo toàn. Các trường bảo toàn thường gặp trong x mMG f .!/ D ˇ!ˇ D p ˇx ˇ mMG Vật lý. x2 C y2 C z2 GIẢI TÍCH B2 266/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường TÍCH PHÂN ĐƯỜNG CỦA HÀM SỐ (Tích Phân Đường Loại I) Cho đường cong C có phương trình tham số x D x.t/; y D y .t/; a Ä t Ä b (4.1) hoặc phương trình vectơ !.t/ D x.t/! C y .t/!, và giả sử C là trơn r i j (nghĩa là r!0 liên tục và !0 .t/ ¤ !). Nếu r 0 ta chia đoạn tham số Œa; b thành n đoạn con Œti 1 ; ti có độ dài bằng nhau và đặt xi D x.ti /, yi D y .ti / thì các điểm P.xi ; yi / chia C thành n cung có độ dài s1 ,. . . , Xn sn . Chọn điểm tùy ý Pi .xi ; yi / (tương tổng f .xi ; yi /si tương ứng với tham số ti 2 Œti 1 ; ti ). Giả sử một iD1 hàm số hai biến f xác định trên C thì tự tổng Riemann của hàm số một biến. GIẢI TÍCH B2 267/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường Định nghĩa Giả sử f là hàm số hai biến, xác định trên đường cong C cho bởi (4.1). Ta định nghĩa tích phân đường của f dọc theo C là Z n X f .x; y / ds D lim f .xi ; yi /si C n!1 iD1 miễn là giới hạn tồn tại. Điều kiện đủ để giới hạn tồn tại là hàm f liên tục. Khi đó, tích phân đường được tính theo công thức Z Z b f .x; y / ds D r r f !.t/ ˇ!0 .t/ˇ dt ˇ ˇ C a r Z b dx Á2 dy Á2 D f x.t/; y .t/ C dt a dt dt GIẢI TÍCH B2 268/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường Nếu f là hàm số 3 biến xác định trên đường cong C -3-chiều, trơn từng ! ! ! khúc, biểu diễn bởi !.t/ D x.t/ i C y .t/ j C z.t/ k , a Ä t Ä b, thì tích r phân đường của f dọc theo C cũng được định nghĩa tương tự. Hơn nữa, nếu f liên tục thì ta cũng có công thức Z Z b f .x; y ; z/ ds D r r f !.t/ ˇ!0 .t/ˇ dt ˇ ˇ C a r Z b dx Á2 dy Á2 dz Á2 D f x.t/; y .t/; z.t/ C C dt a dt dt dt GIẢI TÍCH B2 269/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường Nếu C là đường cong trơn từng khúc, nghĩa là C là hợp của hữu hạn đường cong trơn, C1 ; C2 ; : : : ; Cn , trong đó điểm cuối của Ci 1 là điểm đầu của Ci , thì ta định nghĩa Z n XZ f ds D f ds C iD1 Ci GIẢI TÍCH B2 270/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường Ví dụZ Tính 2x ds, trong đó C bao gồm cung C1 của parabola y D x 2 từ C .0; 0/ đến .1; 1/, được nối tiếp sau đó đoạn thẳng C2 từ .1; 1/ đến .1; 2/. Giải. Ta có C1 W x D x; y D x 2 ; 0 Ä x Ä 1. Do đó Z Z 1 r dx Á2 dy Á2 2x ds D 2x C dx C1 0 dx dx Z 1 p 1 5p Z D 2x 1 C 4x 2 dx D t dt 0 4 1 p 1 3 ˇ5 5 5 1 D t 2ˇ D ˇ 6 1 6 GIẢI TÍCH B2 271/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường Tương tự, C2 W x D 1; y D y ; 1 Ä y Ä 2 và Z Z 2 s dx Á2 dy Á2 2x ds D 2.1/ C dy C2 1 dy dy Z 2 D 2 dy D 2 1 Vậy p p 5 5 1 11 C 5 5 Z 2x ds D C2D C 6 6 GIẢI TÍCH B2 272/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường TÍCH PHÂN ĐƯỜNG CỦA TRƯỜNG VECTƠ (Tích Phân Đường Loại II) ! Nhắc lại, lực F tác động vào vật dịch chuyển từ A đến B thì công của ! ! lực trên đoạn đường đó là W D F AB. ! ! ! ! Giả sử, F D P i C Q j C R k là một trường vectơ lực 3 chiều, ví dụ như trường lực hấp dẫn. (2 chiều ứng với R D 0). Để tính công của trường lực này tác động vào một chất điểm dịch chuyển trên đường cong trơn C , 3-chiều, ta chia C thành nhiều cung nhỏ Pi 1 Pi có độ dài si , bằng cách chia đều đoạn tham số Œa; b thành nhiều đoạn con. Trên cung nhỏ thứ i, ta chọn điểm Pi .xi ; yi ; zi / tương ứng với giá trị ti của tham số. Lộ trình trên cung từ Pi 1 đến Pi xấp xỉ với đoạn thẳng dài ! si , theo hướng của T .ti /, vectơ tiếp tuyến đơn vị của C tại điểm Pi . GIẢI TÍCH B2 273/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân 4.2. Tích phân đường ! Do đó công của lực F tác động vào chất điểm di chuyển trên cung Pi 1 Pi được tính xấp xỉ bằng ! ! ! ! F .xi ; yi ; zi / si T .ti / D F .xi ; yi ; zi / T .ti / si và công dịch chuyển trên toàn C được xấp xỉ bởi n X ! F .xi ; yi ; zi / !.ti / si T (4.2) iD1 ! Công của trường lực F được định nghĩa là giới hạn của tổng Rie- mann (4.2), khi n ! 1, nghĩa là Z Z ! W D F .x; y ; z/ T .x; y ; z/ ds D ! ! ds ! F T (4.3) C C GIẢI TÍCH B2 274/??