TÍCH PHÂN BỘI
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân
3.1. Tích phân kép trên một hình chữ nhật
THỂ TÍCH VÀ TÍCH PHÂN KÉP
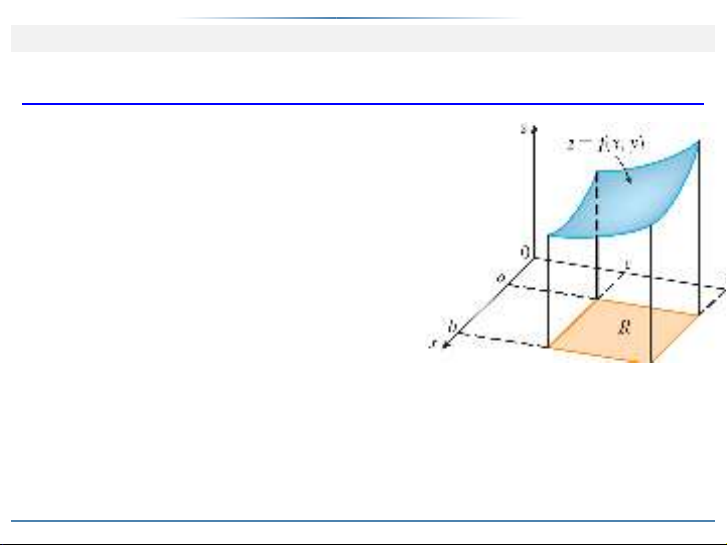
Hình bên là đồ thị của một hàm số f
không âm, xác định trên hình chữ
nhật R
RDŒa;bŒc;d
D˚.x;y/2R2ˇˇaxbvà cyd
Đồ thị là mặt cong có phương trình
zDf.x;y/.
Gọi Slà khối nằm dưới đồ thị của fvà nằm trên hình chữ nhật R
SD˚.x;y;z/2R3ˇˇ0zf.x;y/; .x;y/2R
Mục này của chương muốn đưa ra định nghĩa thể tích của khối S.
GIẢI TÍCH B2 180/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân
3.1. Tích phân kép trên một hình chữ nhật
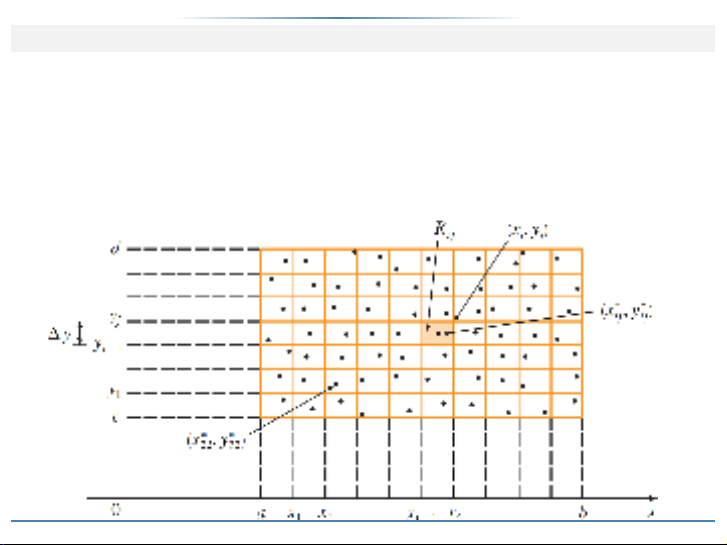
Chia đoạn Œa;bthành mđoạn con Œxi1;xiđều nhau với độ dài
xD.ba/=m; chia đoạn Œc;dthành nđoạn con Œyj1;yjđều nhau với
độ dài yD.dc/=n. Như vậy ta có mn hình chữ nhật con có dạng
Rij DŒxi1;xiŒyj1;yjD˚.x;y/ˇˇxi1xxi;yj1yyj
với diện tích ADxy.
GIẢI TÍCH B2 181/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân
3.1. Tích phân kép trên một hình chữ nhật
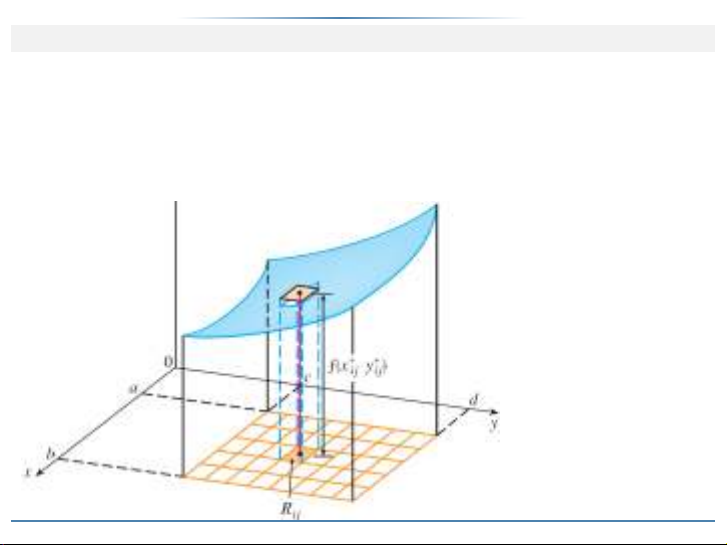
Trên mỗi ô con Rij , chọn một điểm mẫu .x
ij ;y
ij /ngẫu nhiên. Ta có thể
xấp xỉ một phần thể tích của khối S nằm phía trên ô con Rij bằng thể tích
cột dạng hộp có đáy Rij và chiều cao bằng f.x
ij ;y
ij /. Thể tích này bằng
f.x
ij ;y
ij /A
GIẢI TÍCH B2 182/??
Đường & Mặt Đạo hàm riêng & Sự khả vi Tích phân bội Giải tích vectơ Làm quen phương trình vi phân
3.1. Tích phân kép trên một hình chữ nhật
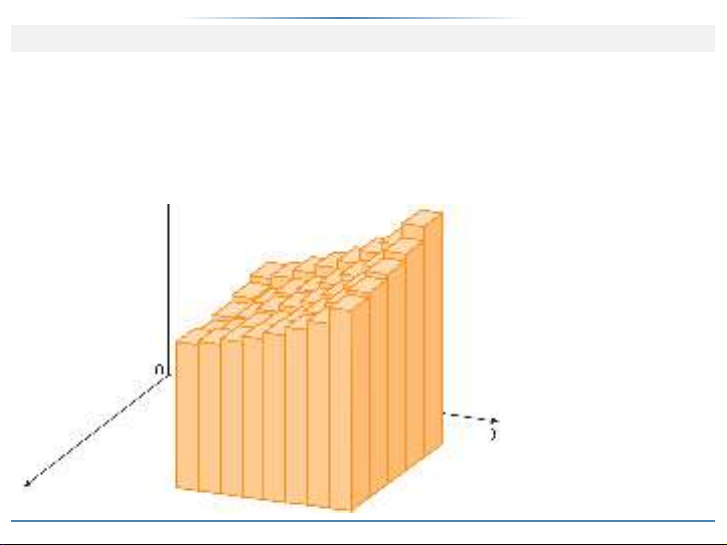
Và thể tích toàn khối S được xấp xỉ bởi
V
m
X
iD1
n
X
jD1
f.x
ij ;y
ij /A
GIẢI TÍCH B2 183/??