
Giáo án đại số 12: §3 PHƯƠNG TRÌNH MẶT PHẲNG
(Tiết 3)
A. Mục tiêu :
1, Về kiến thức: Công thức khoảng cách từ 1 điểm tới 1
mặt phẳng
2, Về kĩ năng: Nhớ và vận dụng được công thức tính
khoảng cách từ 1 điểm đến 1 mặt phẳng và áp dụng vào các bài
toán khác.
3, Về tư duy, thái độ: Cẩn thận, chính xác trong việc vận
dụng công thức, tính toán.
B. Chuẩn bị:
- Giáo viên : giáo án, máy chiếu projector, thước..
- Học sinh: dụng cụ học tập, sách, vở,…
C. Phương pháp:
- Tích cực hóa hoạt động của học sinh
D. Tiến trình:
1. Ổn định lớp
2. Nội dung cụ thể:
Hoạt động 1: Kiểm tra bài cũ

Ho
ạt động của
Giáo Viên
Hoạt động của
học sinh Ghi bảng
7’
GV chi
ếu câu
hỏi kiểm tra b
ài
cũ lên màn hình:
GV nh
ận xét, sửa
sai( nếu có) v
à
cho điểm.
- Học sinh lên
bảng làm bài
Câu hỏi kiểm tra b
ài
cũ:
- Viết phương tr
ình
mặt phẳng (α)
đi qua 3
đi
ểm A(5,1,3) ;
B(5,0,4) ; C(4,0,6)
- Xét vị trí tương đ
ối
giữa (α) và (
β): 2x + y
+ z + 1 = 0
Hoạt động 2: Công thức khoảng cách từ 1 điểm tới 1 mặt
phẳng
Ho
ạt động của
Giáo Viên
Hoạt động của
học sinh Ghi bảng
6’ Hỏi: Nh
ắc lại
công th
ức
khoảng cách t
ừ 1
Cho M(x0,y0) và
đường thẳng :
ax + by + c = 0
4. Kho
ảng cách từ 1
điểm tới 1 mặt phẳng
đi
ểm đến 1
đư
ờng thẳng
trong hình h
ọc
phẳng?
GV nêu công
th
ức khoảng
cách t
ừ 1 điểm
t
ới 1 mặt phẳng
trong không gian
GV hư
ớng dẫn
sơ lư
ợt cách
ch
ứng minh công
thức v
à cách ghi
nhớ
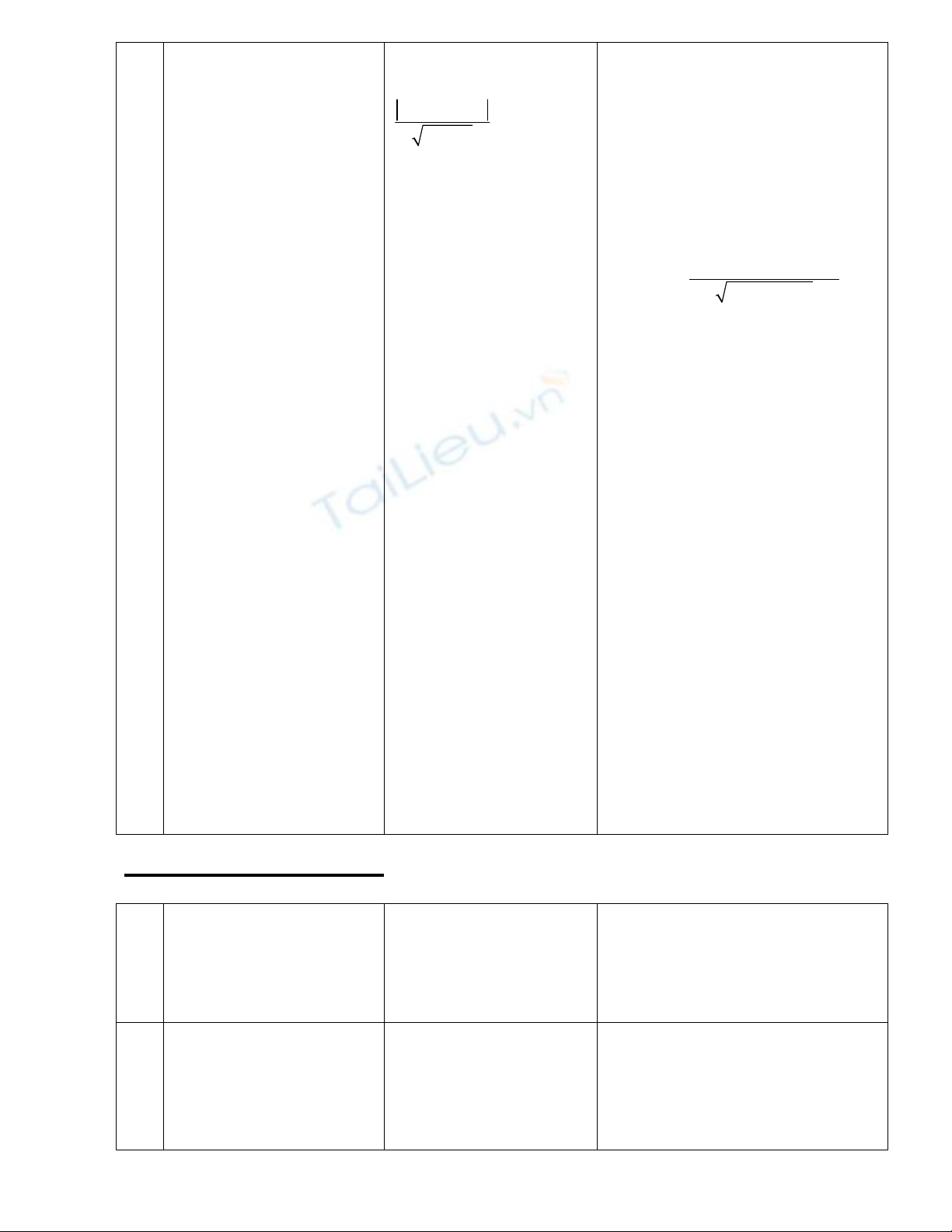
d( M; ) =
0 0
2 2
ax
by c
a b
Xét M0(x0,y0,z0
) và
mp(
): Ax + By + Cz
+ D = 0, ta có công
thức:
0 0 0
0222
Ax + By +Cz + D
d M ,a = A +B +C
Hoạt động 3: Ví dụ 1
Ho
ạt động của
Giáo Viên
Hoạt động của
học sinh Ghi bảng
6’ GV chi
ếu câu
hỏi của ví dụ 1
- Hs theo dõi
Ví d
ụ 1: Tính khoảng
cách giữa 2 mặt phẳng

H
ỏi: Theo câu
hỏi kiểm tra b
ài
cũ, ta đã có (
α)
//(β). N
êu cách
xác đ
ịnh khoảng
cách gi
ữa 2 mặt
phẳng đó?
G
ọi 1 học sinh
lên bảng giải
Nhận xét
+ Lấy 1 điểm A
bất kì thuộc (α) .
Khi đó:
d((α) ,(β)) =
d(A,(α))
HS lên bảng
(α) : 2x + y + z –
14 =
0
(β): 2x + y + z + 1 = 0
Hoạt động 4: Ví dụ 2
Ho
ạt động của
Giáo Viên
Hoạt động của
học sinh Ghi bảng
12
’
GV chi
ếu câu
hỏi của ví dụ 2
OH là đư
ờng
cao cần tìm
Ví d
ụ 2: Cho tứ diện
OABC có OA
vuông
góc với(O
BC). OC =
Hỏi: N
êu các
cách tính?
GV hư
ớng dẫn
h
ọc sinh cách 3:
sử dụng ph
ương
pháp tọa độ
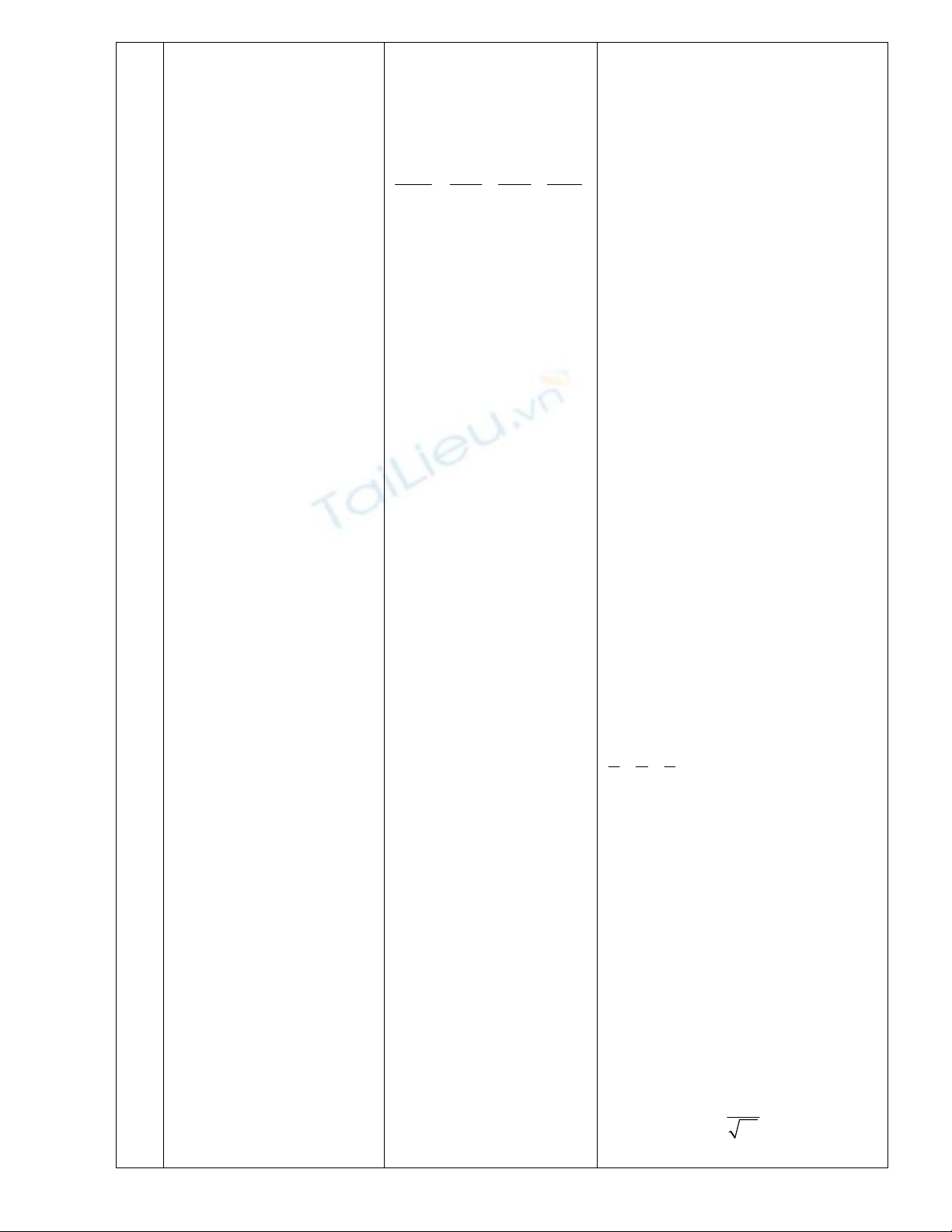
Cách 1:
2 2 2 2
1 1 1 1
OH OA OB OC
Cách 2: Dùng
công th
ức thể
tích
OA = 4cm, OB = 3 cm,
BC = 5 cm. Tính đ
ộ
dài đư
ờng cao của tứ
diện kẻ từ O.
Giải:
Tam giác OBC vuông
tại O( Pitago) n
ên OA,
OB, OC vuông góc đ
ội
một.
Ch
ọn hệ trục tọa độ có
gốc là O và A= (0,0,4),
B= (3,0,0), C =(0,4,0)
Pt mp(ABC) là :
1 0
344
x y z
4x + 3y + 3z – 12 = 0
OH là đư
ờng cao cần
tìm
Ta có : OH = d(O,
(ABC))
=
12
34


























