
ÔN TẬP CHƯƠNG II (tt)
I. Mục tiêu:
+ Về kiến thức:
- Hệ thống các kiến thức cơ bản về mặt tròn xoay và các yếu tố
cơ bản về mặt tròn xoay như trục, đường sinh,...
- Phân biệt được các khái niệm về mặt và khối nón, trụ, cầu và
các yếu tố liên quan.
- Nắm vững các công thức tính diện tích xung quanh và thể tích
của khối nón, khối trụ, công thức tính diện tích mặt cầu và thể tích
khối cầu.
+ Về kỹ năng:
- Vận dụng được các công thức vào việc tính diện tích xung
quanh và thể tích của các khối : nón, trụ, cầu.
- Rèn luyện kĩ năng vẽ hình cho học sinh.
+ Về tư duy và thái độ:
- Rèn luyện tính tích cực, sáng tạo, cẩn thận.
II. Chuẩn bị của giáo viên và học sinh:

+ Giáo viên:Giáo án, bảng phụ, phiếu học tập.
+ Học sinh: Dụng cụ học tập, SGK,...
III. Phương pháp: Gợi mở, giải quyết vấn đề.
IV. Tiến trình bài học:
Tiết 1:
1. Ổn định tổ chức:
2. Kiểm tra bài cũ:
CH1: Ghi các công thức tính diện tích và thể tích các mặt và
khối:nón, trụ, cầu.
Mặt nón-Khối
nón
Mặt trụ-Khối trụ Mặt cầu-Khối cầu
Diện
tích
Sxq= Sxq= S=
Thể tích
V= V= V=
GV chính xác hóa kiến thức, đánh giá và ghi điểm.
3. Bài mới:
* Hoạt động 1: Giải bài toán đúng sai.
TG
Hoạt động của giáo
viên
Hoạt động của học
sinh
Ghi bảng

Đọc đề BT1 SGK
CH1: Qua 3 điểm
A,B,C có bao nhiêu
mặt phẳng.
CH2: Xét vị trí
tương đối giữa mp
(ABC) và mặt cầu
và trả lời câu a.
CH3: Theo đề
mp(ABC) có qua
tâm O của mặt cầu
không.
CH4: Dựa vào giả
thiết nào để khẳng
định AB là đường
kính của đường tròn
+ Xem đề SGK /T50
+ Trả lời: Có duy
nhất mp(ABC)
+ Mp(ABC) cắt mặt
cầu theo giao tuyến
là đường tròn qua
A,B,C. Suy ra kết
quả a đúng.
+ Chưa biết (Có 2
khả năng)
+ Dựa vào CH3 suy
ra: b-Không đúng
c-Không đúng.
+Dựa vào giả thiết:
ABC =900 và kết quả
câu a
hay không.
*Hoạt động 2: Kết hợp BT2 và BT5 SGK/T50
T
G
Hoạt động của giáo
viên
Hoạt động của học
sinh
Ghi bảng
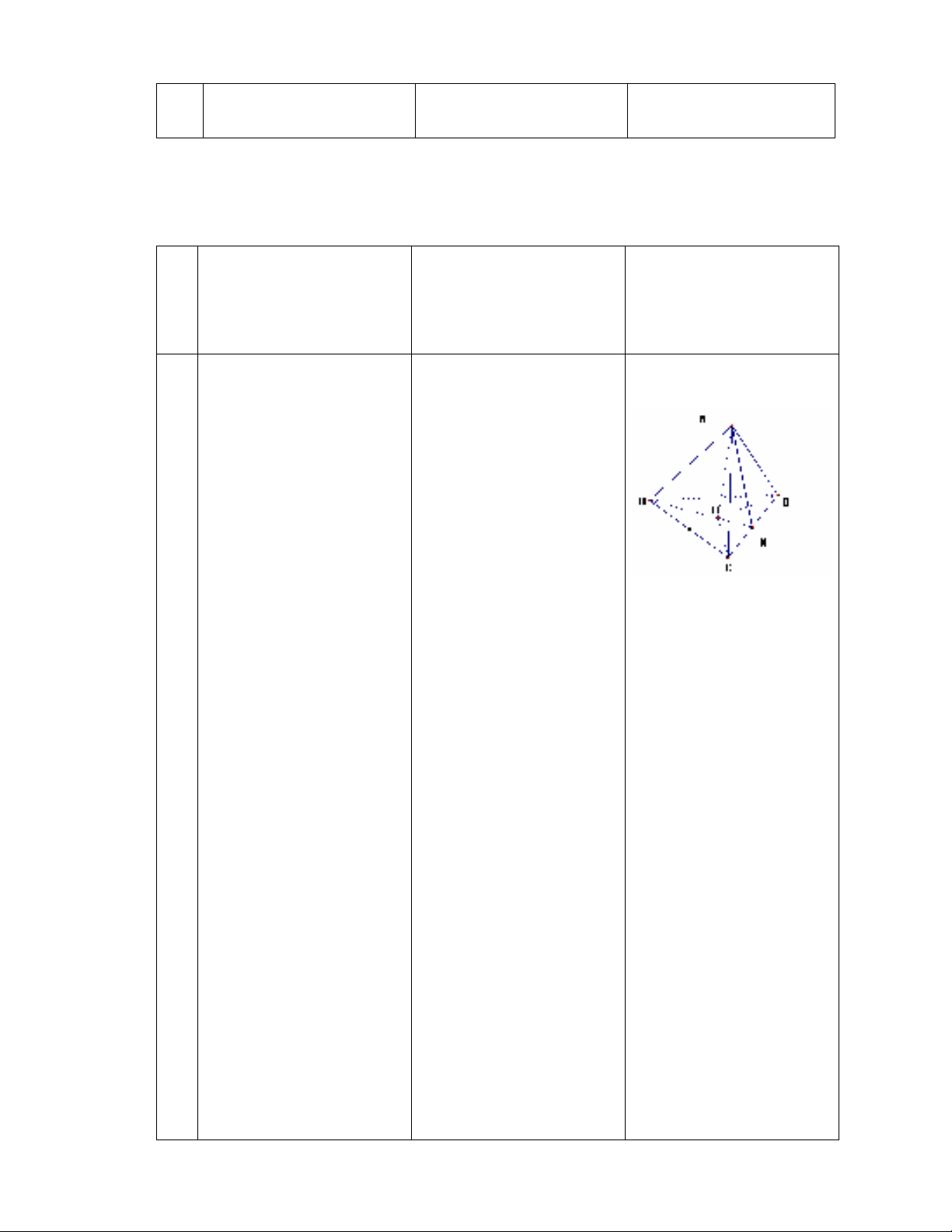
Nêu đề: Cho tứ diện
đều ABCD cạnh a.
Gọi H là hình chiếu
của A trên
mp(BCD). N là
trung điểm CD
a- Chứng minh
HB=HC=HD. Tính
độ dài đoạn AH.
b- Tính Sxq và V
của khối nón tạo
thành khi quay miền
tam giác AHN
quanh cạnh AH.
- Vẽ hình (GV
hướng dẫn nếu cần)
a) AH
(BCD)
=> Các tam giác
AHB, AHC, AHD
vuông tại H
Lại có: AH cạnh
chung
AB=AC=AD(
ABCD là tứ diện

c- Tính Sxq và V của
khối trụ có đường
tròn đáy ngoại tiếp
tam giác BCD và
chiều cao AH.
Hoạt động 2.1:
CH1: Có nhận xét gì
về các tam giác
AHB, AHC, AHD.
Nêu cách tính AH.
TL: Chúng là 3 tam
giác vuông bằng
nhau.
Suy ra HB=HC=HD
AH= 22 BHAB
+Cần xác định độ
đều)
=> 3 tam giác AHB,
AHC, AHD bằng
nhau
Suy ra HB=HC=HD
*AH= 22 BHAB
= 3
2
2a
a=
3
6a
b) Khối nón tạo
thành có:
3
6
6
3
2
3
a
AHh
a
HNr
a
ANl
Sxq=
rl=
.
6
3a.
2
3a
=
4
2
a
V= hB.
3
1
=
3
6
.
12
.
3
12aa
=
108
6
3
a
c) Khối trụ tạo thành


























