
ườ độ Đ ấ đề ế ứ ầ ế đố ớ ạ
đặ đ ể ị ử ấ ượ ồđộ ệườ ấ ớ
ạđộ ả ấ ệ đ ỏ ự ă ặ
ự ủ ườ độ đố ớ ồ ề ườ ợ
ệ ệ ạ ế ả ốươ
ế ụ ươ ụ ạ ở ữ ệ
ỗươ ả ị ộ ứ độ độ
đế ữ ặ ậ ậ ụ ổ ợ ươ ả
ị ả ấ ạ ầ ế
ữườ ợ ấ đị ươ đượ ấ ạ ơ
ươ ư ự ấ ạ đ ũ ỉ ấ ờ ầ ă độ
ế ứ ề ẻ ử ụ ươ độ đế ườ
ả ị ả ấ
CHƯƠNG III. LÝ THUYẾT VỀ HÀNH VI SẢN XUẤT
I. NHỮNG MỐI QUAN HỆ CÓ TÍNH VẬT CHẤT.
Trong chương này chúng tôi trình bày những nội dung chính về lý thuyết của
kinh tế học trong khu vực sản xuất, đã tỏ ra cần thiết trong nghiên cứu về thị
trường nông nghiệp. Cũng như mọi ngành kinh tế khác, kinh tế học trong sản xuất
nông nghiệp cũng quan tâm đến việc phân phối nguồn lực khan hiếm cho nhiều
phương hướng sản xuất. Trong lý thuyết về sản xuất, người ta tìm mọi cách chọn
lựa: Sản xuất cái gì? Sản xuất bao nhiêu và sản xuất như thế nào? Quyết định việc
này bởi chính người sản xuất - được xác định là “một tác nhân cụ thể chuyên trách
việc chuyển đổi các yếu tố đầu vào thành các loại hàng hoá mong muốn, đó là các
yếu tố đầu ra” (Hirshlefer – 1976).
Sản xuất là quá trình phối hợp và điều hoà các yếu tố đầu vào (tài nguyên hoặc
các yếu tố sản xuất như: đất đai, lao động…) để tạo ra các đầu ra (hàng hóa hoặc
dịch vụ như: thóc, ngô, thịt, trứng, sữa…). Chẳng hạn để sản xuất ra một tấn mũ
cao su, ta cần có: các điều kiện khí hậu thích hợp, diện tích đất canh tác, phân bón,
các dịch vụ khác như lao động chăm sóc, thu hoạch… Nếu giả thiết sản xuất sẽ
diễn biến một cách có hệ thống với trình độ sử dụng đầu vào hợp lý, các nhà kinh
tế học thường biểu thị mối quan hệ giữa lượng đầu vào cần thiết và lượng đầu ra
có thể có được bằng các ký hiệu toán học được gọi là “hàm sản xuất”.
Hàm sản xuất là mối quan hệ kỷ thuật biểu thị lượng hàng hóa tối đa có thể
thu được từ các kết hợp khác nhau của các yếu tố đầu vào với một trình độ công
nghệ nhất định.
Hàm sản xuất tổng quát có dạng:
Q = f (X1, X2, X3,... Xn)
Trong đó: Q: Sản lượng đầu ra.
X1, X2, X3,... Xn: Các yếu tố đầu vào được sử dụng trong quá trình sản xuất.

Hàm sản xuất có thể được biểu diễn bằng một phương trình, một bảng số liệu
hay một đồ thị nào đó. Để hiểu thêm về hàm sản xuất ta lấy ví dụ như sau: Giả sử
có một nhà máy may quần áo, để đơn giản ta chỉ xét 2 yếu tố đầu vào là lao động
và máy khâu. Sự kết hợp giữa lao động và máy khâu cho chúng ta các kết quả đầu
ra khác nhau, thể hiện ở biểu sau:
Biểu 1.1: Hàm sản xuất với hai đầu vào là máy khâu và lao động.
Số lao động mỗi ngày
Số máy khâu 0 1 2 3 4 5 6
0 0 0 0 0 0 0 0
1 0 15 34 44 48 50 51
2 0 20 46 64 72 78 81
3 0 21 50 79 82 92 99
Qua biểu trên ta thấy, nếu không có lao động và không có máy khâu nào thì tất
nhiên không tạo ra được sản phẩm, nói cách khác không có đầu vào thì cũng
không có đầu ra. Với một máy khâu và một lao động, doanh nghiệp có thể sản
xuất tối đa 15 bộ quần áo mỗi ngày; với 2 máy khâu và 2 lao động doanh nghiệp
sản lượng tối đa là 46 bộ quần áo… Cần lưu ý rằng mức sản lượng nói trên chỉ đạt
được khi doanh nghiệp tổ chức sản xuất và quản lý thật tốt.
Như vậy, hàm sản xuất cho chúng ta biết một khái niệm có tính chất thuần túy
vật chất, nhằm mô tả lượng đầu ra tối đa về vật chất với việc sử dụng một hoặc
một số yếu tố đầu vào nhất định về vật chất. Trình độ kết hợp giữa các yếu tố đầu
vào trong sản xuất quyết định hiệu quả kinh tế trong việc sử dụng các yếu tố đó.
Hơn nữa trong nền kinh tế thị trường, mọi hàng hóa được sản xuất ra để trao đổi,
lưu thông, do vậy đầu ra của sản xuất cũng phải hướng theo nhu cầu thị trường và
việc xác định cơ cấu sản phẩm hợp lý trong mối quan hệ với các nguồn tài nguyên
khan hiếm cũng có ý nghĩa kinh tế quan trọng.
Trong phần này, chúng ta sẽ xem xét những mối quan hệ có tính vật chất giữa
các yếu tố sản xuất với sản phẩm được sản xuất ra, giữa các yếu tố sản xuất với
nhau và giữa sản phẩm với sản phẩm.
1.1. Mối quan hệ giữa yếu tố sản xuất và sản phẩm sản xuất ra (sản xuất
với một đầu vào biến đổi).
Vấn đề ở đây là nghiên cứu từng yếu tố sản xuất đã tác động đến lượng sản
phẩm Q như thế nào? Để đạt được điều đó ta giả thiết rằng chỉ có một yếu tố biến
đổi tác động đến Q, chẳng hạn yếu tố x1, còn các yếu tố khác của hàm sản xuất
không đổi. Ta có hàm sản xuất:
Q = f (X1/ X2, X3,... Xn)
X1: đứng trước ký hiệu / là yếu tố sản xuất biến đổi;

X2, X3,... Xn: đứng sau kí hiệu / là các yếu tố sản xuất không biến đổi.
Biểu 1.2: Sản xuất với một đầu vào biến đổi (Lao động)
Tổng số
lao động (L)
Tổng số
vốn (K)
Tổng số
Độngầu ra
(Q)
Năng suất
B.quân (Q/L)
Năng suất cận
biên (∆Q/∆L)
0 10 0 - -
1 10 10 10 10
2 10 30 15 20
3 10 60 20 30
4 10 80 20 20
5 10 95 19 15
6 10 108 18 13
7 10 112 16 4
8 10 112 14 0
9 10 108 12 -4
10 10 100 10 -8
Ví dụ: Chúng ta hãy xem xét trường hợp trong đó vốn là yếu tố sản xuất cố
định, còn lao động là yếu tố sản xuất biến đổi sao cho doanh nghiệp có thể sản
xuất nhiều đầu ra hơn bằng cách tăng số lao động đầu vào.
Biểu số liệu 1.2 cho thấy tổng số đầu ra có thể được sản xuất với những số lao
động khác nhau và với một số vốn cố định là 10 đơn vị. Khi số lượng lao động là
0, số đầu ra cũng là 0. Sau đó khi số lao động tăng lên đến mức 8 đơn vị thì số đầu
ra tăng lên vì số lao động được gia tăng. Vượt quá điểm ấy, tổng số đầu ra giảm
sút. Như vậy, trong khi lúc đầu mỗi đơn vị lao động có thể lợi dụng được lợi thế
của máy móc và thiết bị hiện có, thì sau một điểm nào đó, số lượng lao động tăng
thêm không còn có ích nữa và có thể phản tác dụng.
Để nghiên cứu mối quan hệ trên ta cần làm rõ một số khái niệm sau:
1.1.1. Tổng sản phẩm (TP: Total product).
Tổng sản phẩm là đại lượng cho biết tổng số đầu ra được sản xuất, theo đơn vị
hiện vật.
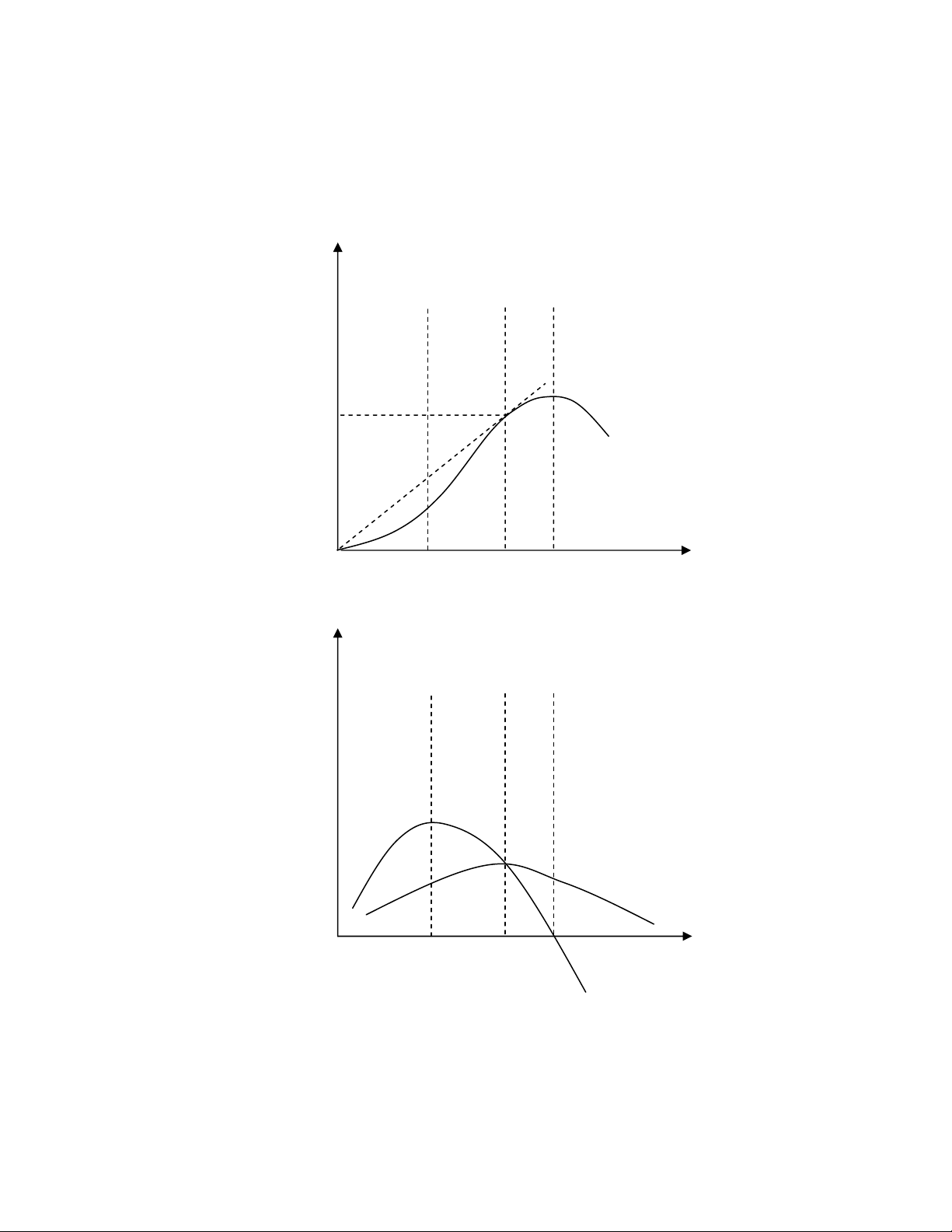
Biểu diễn hàm sản xuất lên đồ thị ta có đường cong tổng sản phẩm (Hình 1.1a).
1.1.2. Sản phẩm bình quân (AP: Average product).
Sản phẩm bình quân của một đầu vào biến đổi là sản lượng tính cho 1 đơn vị
yếu tố đầu vào đó đã được sử dụng.
Sản phẩm bình quân (AP) = Số lượng đầu ra (Q)/ số lượng đầu vào biến đổi
(X1)

Hay nói cách khác sản phẩm bình quân chính là độ nghiêng của đường thẳng đi
qua gốc tọa độ và điểm quan sát trên đường cong tổng sản phẩm. Chẳng hạn, sản
phẩm bình quân của yếu tố đầu vào X1 tại mức khối lượng X1’’’ là độ nghiêng của
đường thẳng OA và đó chính là độ nghiêng lớn nhất hay điểm có sản phẩm bình
quân cực đại (hình 1.1b).
1.1.3. Sản phẩm cận biên (MP: Marginal product).
Người sản xuất luôn tìm kiếm liệu chi phí đầu tư tăng thêm có đem lại sản
lượng sản phẩm tương ứng hay không, cứ mỗi lần tăng thêm một lượng X1 nhất
định có thể thu được một lượng sản phẩm tăng bổ sung, phần sản phẩm tăng thêm
đó gọi là sản phẩm cận biên. Nếu X1 biến đổi một lượng ∆X1 thì Q cũng biến đổi
một lượng ∆Q tương ứng. Như vậy:
Sản phẩm cận biên của một yếu tố đầu vào biến đổi là mức sản phẩm tăng
thêm hay giảm đi khi sử dụng thêm một đơn vị yếu tố đầu vào biến đổi đó trong
điều kiện giữ nguyên mức sử dụng các yếu tố đầu vào cố định khác.
Sản phẩm cận biên của X1 = Thay đổi tổng sản phẩm/ Thay đổi lượng đầu vào
X1
MPX1 = Q/ X1
Nếu ∆X1 vô cùng nhỏ thì sản phẩm cận biên chính là đạo hàm bậc nhất của
hàm sản xuất, bằng độ dốc của đường cong tổng sản phẩm (đường cong biểu diễn
hàm sản xuất) tại điểm quan sát, ta có thể viết như sau:
MPX1 = ∂Q/ ∂X1
Đặc biệt nếu ∆X1= 1 MPX1 = Qn +1 - Qn
Ta cũng vẽ được đường cong sản phẩm cận biên (hình 1.1b); theo tính chất của
đạo hàm bậc nhất ta có:
MPX1 đạt cực đại tại điểm uốn của đường cong tổng sản phẩm khi X1 = X1’;
MPX1 < 0 khi X1 > X1’’;
MPX1 = 0 tại điểm cực đại của đường cong tổng sản phẩm khi X1 = X1’’.
Như vậy, khi X1 chạy từ 0 đến X1’ thì MPX1 tăng dần và đạt cực đại tại X1’; khi
X1 chạy từ X1’ đến X1’’ thì MPX1 giảm dần và bằng 0 khi X1 = X1’’; sau đó MPX1
< 0 đường cong sản phẩm cận biên nằm dưới trục hoành khi X1 > X1’’.
1.1.4. Quy luật năng suất cận biên giảm dần.
Quy luật năng suất cận biên giảm dần được phát biểu như sau:
Tổng
sản phẩm
Hình 1.1a: Đường cong tổng sản phẩm
Mức
độ 3
TP
0 X1’ X1’’’ X1’’ X1
Mức độ 1 Mức độ
2
Mức độ 4
AP
MP Mức
độ 2
Mức
độ 3
Mức độ 1 Mức độ 4
MP
0 X1’ X1’’’ X1’’
AP
X1
Hình 1.1b: Đường cong sản phẩm cận biên và sản phẩm bình quân






















