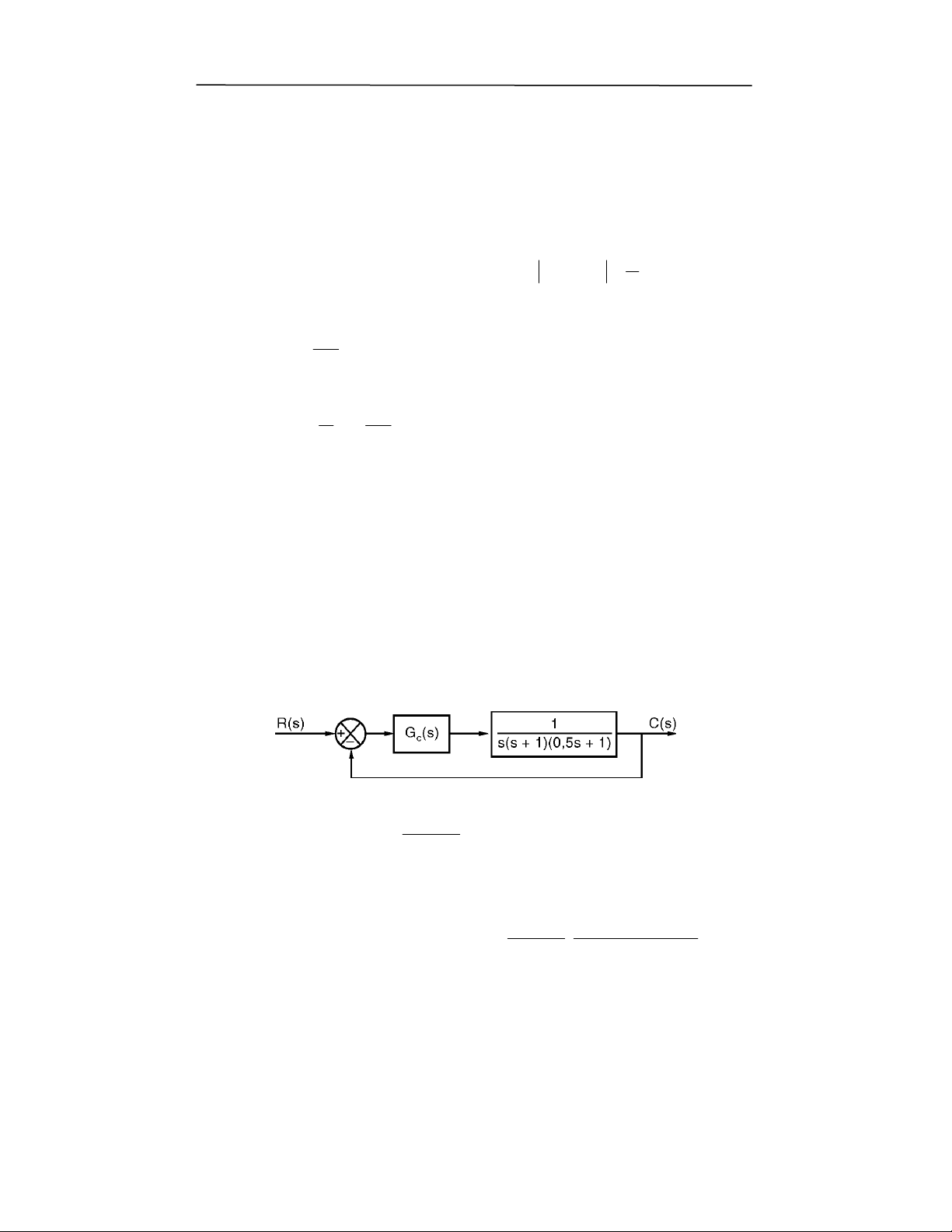
1
'<
% >M
h 8  ' 7 1
′
ω
($8   6 $ %  $
( ^ ,7A " #$%  k
*
( )
′
ϕ ω = − ° + Φ + θ
N< 
,:0)"0
*
Φ
/ A" 0  @71 ,:7P 9 !0 )! $0; d
2 '<
%EM
")
α
,7 A" # $% k
( ) lg
′
ω = − α
'<
0K(
P d
( )
′
ω =
α
%3M
:.-U.D360(0k
"
′
<< ω
α
⇒
"
α

%TM
")X'"
" "
= α
α
⇒
"
%UM
 &!,: /1  ,0; )(0 , 08 ! P" #$%  > #"0 
@71,:7PR+*%0+)b;$%0+),08!P,L,:F8/1R7F(
+ M
:0 ) ,:7 FA) F1 9  ,0; ) O$  9 7( ,1 9 %0  ,L!
"7F1(/FA)8)8,?(,L(0,&Q("5
( )
′
ϕ ω
]
′
ω
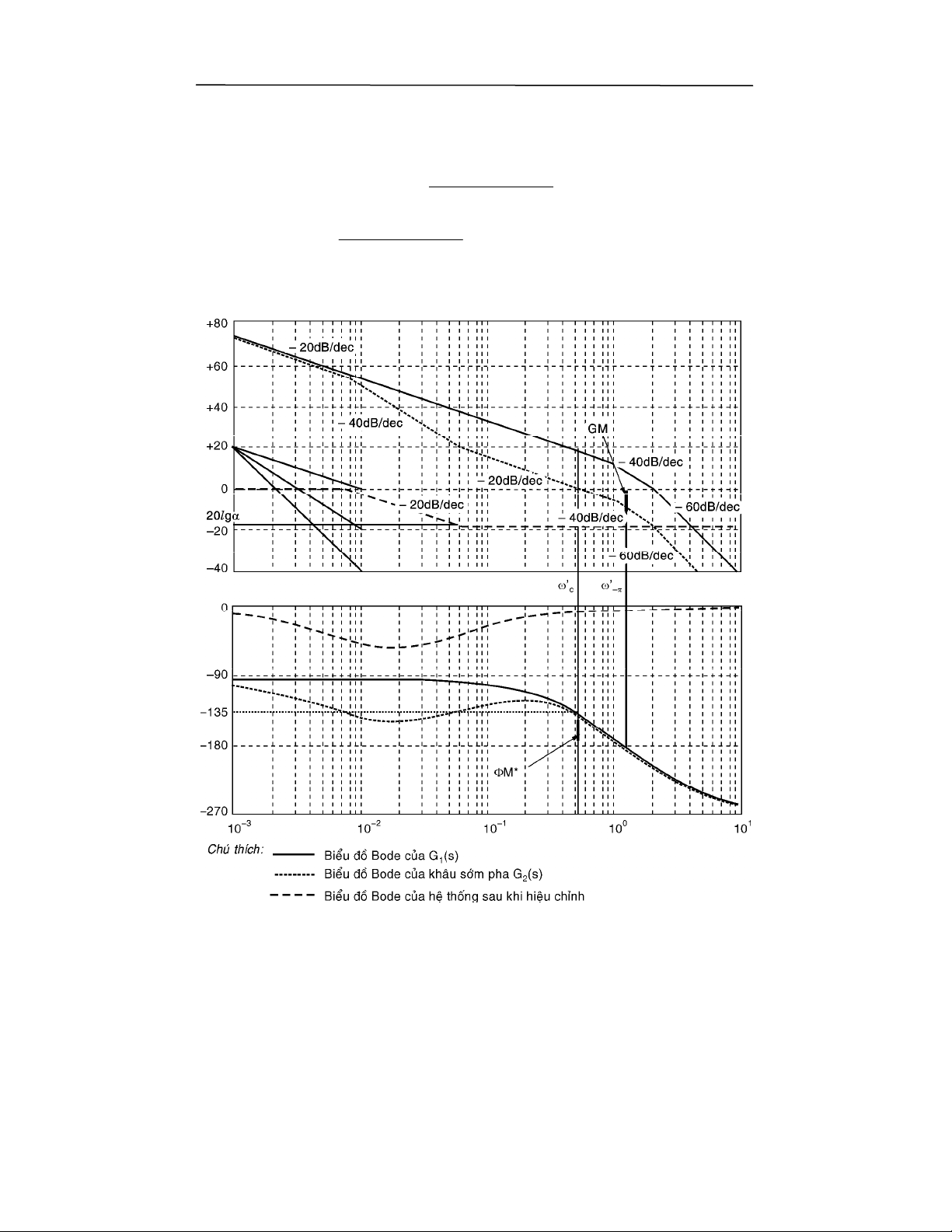
gR7F(h>A
( )
′
ω
gR7F(3hRY)((@71>A0R&$"0#T0@
PC GB T6
5
6
" - -  U .D 3  3 33
12#0
P* , ;,% ;% +$   $( ^ ,: j9 6 0( 0 , 0; )6 $
%  $ (^ ( 0k
Y
&*
;
=
2
*
;
Φ ≥
3<
P #
*≥< 
-6
A !,: $* # %+$   $ (^ , :j 9 (# , ; ,% ;/ Ak
"'
P ' &
"'
( )
+ α
=+
g
α <
h
%5M
h8&
 6 0;>   ,0;( ($8   6 $ %  $( ^ /A k

Y
' '
"'
& 'P ' P ' '& &
"' ' ' '
*
lim ( ) ( ) lim . ( )( , )
→ →
+ α
= = =
+ + +
< <
< 2 
$!
'
⇒
Y
& &
*
=⇒
&
=
2
%1
K,k
P ' & P ' ' ' '
( ) ( ) .
( )( , )
= =
+ +
2
< 2
⇒  P ' ' ' '
( )
( )( , )
=
+ +
2
< 2
T&$"0#T0@($8
P '
( )
gE'h
+,5.2
#2# .4'-U.D3

1
''
%>M
h8'76
L!
′
ω
RY)97F)99)8,?((0k
*
( )
′
ϕ ω = − ° + Φ + θ
N<
⇒
a r ct a n ( ) a r ct a n ( , )
′ ′
− ° − ω − ω = − ° + ° + °
< < 2 N< 3< 2
⇒
a r ct a n ( ) a r ct a n ( , )
′ ′
ω + ω = °
< 2 32
⇒
( ) ( , ) ta n ( )
, ( )
′ ′
ω + ω
= ° =
′
− ω '
< 2
32
< 2
⇒
, ( ) ,
′ ′
ω + ω − =
'
< 2 2 <
⇒
,
′
ω =
< 2E
g. e'h
U71>A0R&$"0#T0@
(0k
*
( )
′
ϕ ω = − ° + Φ + θ
N<
⇒ 
( )
′
ϕ ω = − ° + +
N< 3< 2
⇒ 
( )
′
ϕ ω = − °
2
 P" 7FA ), ` )(0 0 A "0 r 2
<
 0A "0 ) 0" &! ( $8
"7FA),`)A*>FR&$"0#T0@>#9
( )
ϕ ω
(?/A),:5
,#60;(-,!F
0LE',,;*k
,
′
ω ≈
< 2
g. e'h
%E
?α ,7A " #$%  k
P d
( )
′
ω =
α
⇒
' d
' ' '
( )( , )
′
= ω
=
+ + α
2
< 2
⇒d d d
, ( , )( , , )
=
+ × + α
2
< 2E < 2E < 2 < 2E
⇒
, ( , )( , )
=
α
+ +
' '
2
< 2E < 2E < 'N
⇒
, , ,
=
× × α
2
< 2E 3E <N ⇒
,
α =
< 
$!
'
?α ,7A " #$%  k
( ) lg
′
ω = − α
'<
U71>A0R&$"0#T0@,,;*k
( )
′
ω ≈
N
@T
H$*:k
lg
= − α
N '<
⇒ 
lg ,
α = −
<
⇒ 
,
−
α =
<
<
⇒ 
,
α =
< 'E
,;*),:5
α
,?,0((%0+)6%($
") %& C (( R7F( ,;, %; ,;9 ,0 , 678 @$1) ) ,:5
,
α =
< 

%3M
:.-.D3

"
,
′
<< ω =
α
< 2E
01
"
,
=
α
< <2
⇒ 
"
α =
'<
%TM
")X"

" "
, , ,
= α = × =
α
<  < <2 < <EG
⇒ 
"
=
2<
  *k 
'
P ' '
( )
( )
( )
+
=
+
'<
2
2<
%UM
&26.-1
U7 1 > A0 R &$ "0# T0@ , ,; * " 0  @ 71 ,:7P R + 6$ %  $
(^/Ak
P #
*≈<
N<M
 +$  $ ( ^ > 7A  , ; , %; " 1, * +$ ( #$ ># "0 @71
,:7PR+
/I
S$  > ?@ $1, ;, % ;% +$ $( ^ 6F !9 > A,: j9 
@$ A) 97 F) 9 9R &$ "0 #T0 @ ,( 0  Q ,6 $k 
Z;$Pg'h/A
<<
, LR A , ;, %; % +$  $ ( ^ 6F !
9 >A ,:j 9 0A ,0A (0 ,& )8 "7F1( RY) (( (0+) ,7(
) 8 ,?( dR 7F( >P R &$ "0# T0 @% 0+ ),  , 671 ( #, ; ,
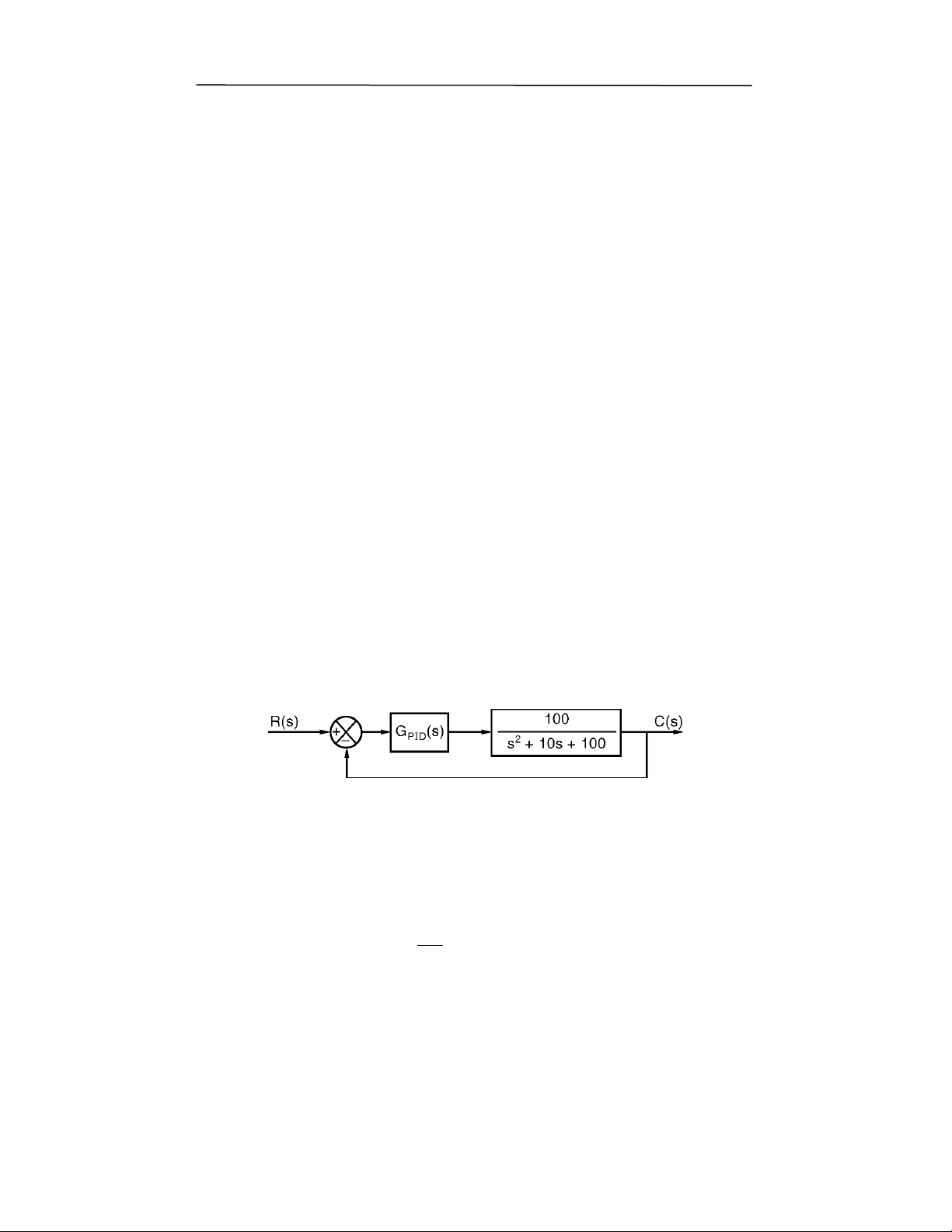
1
'3
Z;$Pg'h/A
<<?
,L(((0+),7()8,?("&
,L! , # 60; (- , R + d , # 6 0; (- , 9 d "0  @71 ,: 7P R + d " 0  @ 71 ,:7P
9q,:F8+97(,19d,:0),:7FA)F19A*+>PR&$"0#T0@
>AQ("5((,0+)60;@71>A0R&$"0#T0@>7A>P
T &$ " 0# T 0@ R +" 0 " 7F1 (>P RY )( (" 7FA) ,  !( d R &$
"0#T0@># 9 "7F1(>PRY)(( 9+ ,?("5 ,?>A,*
!0 ,6 0; ) ,: 5, #6 0;
ω
R&$,7(
( )
ϕ ω
"&(0),:5"5/7F1)
Z &* R f) , 0+) ( $8  6 $%    $ ( ^6 F! 9 > A , :j
9 H $%  $( ^6F !9 R f) , 0+) ( $8  , 0; )"7F1(
!F 8 :0 )d " 9 7 ) ($ 8  "0;  >F  ,?   $ , # 60 ; (0 , 0; , Fd  " 9
7 ) O$  "0 " 7F1( ( 8 , l ,: 0) % "0  6 $ %   $ ( ^ ,: j
9 R f) ,0 +) ( $8  ,0 ;) R 5, $ 19 d" 97 )( $8  "0 ;> F
,?  $,#  60; (0 %! "d " 9 7 ) O$  "0 ($8   , 0;) R 5 (  !
/1 L > * ( # ; ! 1  : Y)  % +$ $ ( ^  6F ! 9  > A
,:j9(0"K("&!0A,0A%($d%0+),&678@$1)/j
/0 " 7F1( 
0)+
T0 "# $% & . U /A ,:7 FA ) F19 "K ( R ,( $8  $ (^ 6 F!
,: j 9  +  > # )$ *+ ,-( (0 ,& , ;, % ; R0 "# $ % &  .U
RY)97F)99@$A)SH0K(@$A)R&$"0#T0@
=0 , 9 7F ) 9 9 %( ($ P) ,7FA ) @$A ) " & , ;, %; R0 "# $
% & . U/A 9 7F )9 9 )8 , ?( H$ "+ */ A! 0 , >? @$1 k
PCGBT6526
 0  , 0; )" #$ % & 7 L > Pk
 P* Q ( "5  , 0+ ) 60 ; ($ 8 R0 " #$ % &  . U 6 0 ( 0  
,0;),08!P*+$(#$k
Z (0 (K 9 ) !9 7( >F 
,
ξ =
< 2
d
ω =
N

Z 60; > ,0 ;(&
Y
p<<
-M
 A! ,:$ *# R0 " #$ % & .U (# , ; ,% ;k
G
_
&
P ' & & '
'
( )
= + +