Giáo trình
Khoa Toán - Tin học
Fac. of Math. & Computer Science
Bộ môn Giải tích
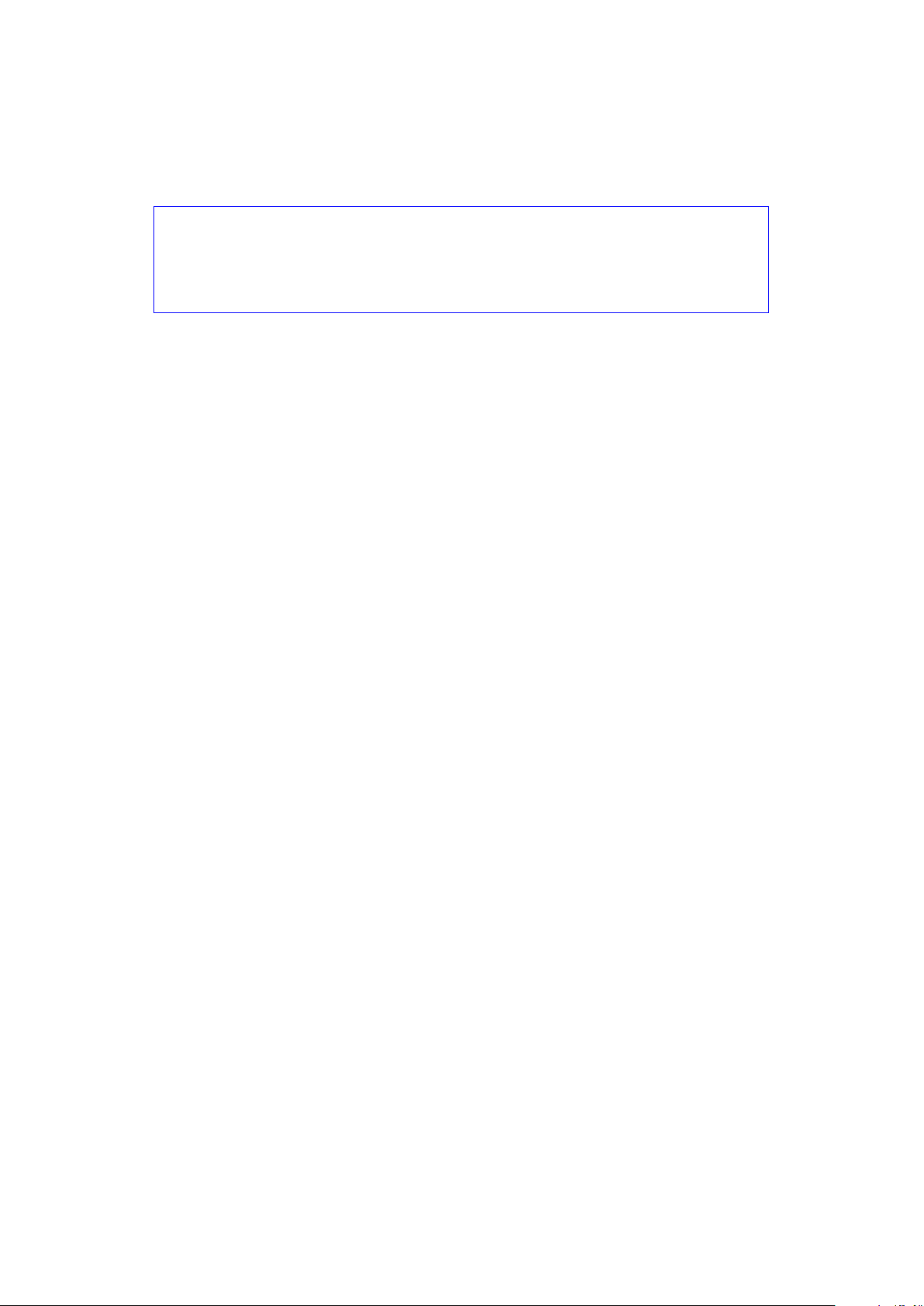
y=b
x=a
z=f(x, y)
z=f(a, b) + fx(a, b)(x−a) + fy(a, b)(y−b)
x
y
z
VI TÍCH PHÂN
2
1
Giáo trình Vi tích phân 2
Bộ môn Giải tích
(Khoa Toán - Tin học, Trường Đại học Khoa học Tự nhiên
Đại học Quốc gia Thành phố Hồ Chí Minh)
Bản ngày 18 tháng 3 năm 2025
Mục lục
Giới thiệu 1
1 Phép tính vi phân của hàm nhiều biến 4
1.1 Không gian Rn.............................. 4
1.1.1 Vectơ, điểm, chiều dài, khoảng cách, tích trong . . . . . . . . 5
1.1.2 Hình học trong Rn........................ 10
1.1.3 Tập mở và tập đóng trong Rn.................. 15
1.2 Hàmsốnhiềubiến ............................ 19
1.2.1 Giới hạn của hàm số . . . . . . . . . . . . . . . . . . . . . . . 21
1.2.2 Hàmsốliêntục.......................... 22
1.3 Đạo hàm của hàm số nhiều biến . . . . . . . . . . . . . . . . . . . . 27
1.3.1 Đạohàmriêng .......................... 27
1.3.2 Xấp xỉ tuyến tính và Mặt phẳng tiếp xúc . . . . . . . . . . . 29
1.3.3 Đạo hàm riêng cấp cao . . . . . . . . . . . . . . . . . . . . . . 33
1.4 Các tính chất của đạo hàm . . . . . . . . . . . . . . . . . . . . . . . 37
1.4.1 Đạo hàm của hàm hợp . . . . . . . . . . . . . . . . . . . . . . 37
1.4.2 Đạo hàm theo hướng . . . . . . . . . . . . . . . . . . . . . . . 40
1.4.3 Đạo hàm của hàm vectơ . . . . . . . . . . . . . . . . . . . . . 44
1.4.4 Đạo hàm của hàm ẩn . . . . . . . . . . . . . . . . . . . . . . 50
1.5 Cực trị của hàm số nhiều biến . . . . . . . . . . . . . . . . . . . . . . 57
1.5.1 Cực trị địa phương . . . . . . . . . . . . . . . . . . . . . . . . 58
1.5.2 Cựctrịtoàncục ......................... 68
2 Tích phân của hàm nhiều biến 80
2.1 Định nghĩa và tính chất của tích phân bội . . . . . . . . . . . . . . . 80
2.1.1 Tích phân trên hình hộp . . . . . . . . . . . . . . . . . . . . 81
2.1.2 Tích phân trên tập tổng quát . . . . . . . . . . . . . . . . . . 85
2.1.3 Thểtích.............................. 85
2.1.4 Tính chất của tích phân . . . . . . . . . . . . . . . . . . . . . 90
2.2 CôngthứcFubini............................. 96
2.2.1 Công thức Fubini cho miền phẳng . . . . . . . . . . . . . . . 99
2.2.2 Công thức Fubini cho miền ba chiều . . . . . . . . . . . . . . 101
ii
MỤC LỤC iii
2.3 Côngthứcđổibiến ........................... 111
2.3.1 Tọađộcực ............................ 113
2.3.2 Tọađộcầu ............................ 117
2.4 Ứng dụng của tích phân bội . . . . . . . . . . . . . . . . . . . . . . . 126
2.4.1 Giá trị trung bình . . . . . . . . . . . . . . . . . . . . . . . . 126
2.4.2 Tâmkhốilượng ......................... 127
2.4.3 Xác suất của sự kiện ngẫu nhiên . . . . . . . . . . . . . . . . 128
3 Giải tích vectơ 137
3.1 Tíchphânđường ............................. 137
3.1.1 Chiều dài của đường đi . . . . . . . . . . . . . . . . . . . . . 137
3.1.2 Tích phân đường loại một . . . . . . . . . . . . . . . . . . . . 140
3.1.3 Tích phân đường loại hai . . . . . . . . . . . . . . . . . . . . 141
3.2 Công thức Newton–Leibniz và Công thức Green . . . . . . . . . . . . 150
3.2.1 Trườngbảotoàn ......................... 150
3.2.2 CôngthứcGreen......................... 154
3.3 Tíchphânmặt .............................. 168
3.3.1 Diệntíchmặt........................... 169
3.3.2 Tích phân mặt loại một . . . . . . . . . . . . . . . . . . . . . 171
3.3.3 Tích phân mặt loại hai . . . . . . . . . . . . . . . . . . . . . . 172
3.4 Công thức Stokes và Công thức Gauss–Ostrogradsky . . . . . . . . . 182
3.4.1 Công thức Stokes . . . . . . . . . . . . . . . . . . . . . . . . 182
3.4.2 Công thức Gauss–Ostrogradsky . . . . . . . . . . . . . . . . . 187
4 Phương trình vi phân 198
4.1 Phương trình vi phân và mô hình toán học . . . . . . . . . . . . . . 198
4.1.1 Mô hình với phương trình vi phân cấp một . . . . . . . . . . 200
4.1.2 Mô hình với phương trình vi phân cấp hai . . . . . . . . . . . 203
4.2 Giải phương trình vi phân cấp một . . . . . . . . . . . . . . . . . . . 206
4.2.1 Phương trình vi phân cấp một tách biến . . . . . . . . . . . . 206
4.2.2 Phương trình vi phân cấp một đẳng cấp . . . . . . . . . . . . 210
4.2.3 Phương trình vi phân cấp một tuyến tính . . . . . . . . . . . 213
4.3 Giải phương trình vi phân cấp hai . . . . . . . . . . . . . . . . . . . 222
4.3.1 Phương trình tuyến tính thuần nhất hệ số hằng . . . . . . . . 222
4.3.2 Phương trình tuyến tính không thuần nhất hệ số hằng . . . . 226
Hướng dẫn sử dụng phần mềm máy tính 235
Tài liệu tham khảo 237
Chỉ mục 239