209
nghị và kể cả so sánh kết quả thu được. Để thiết kế bộ lọc thông cao sử dụng
một trong những phương pháp được cho trong cuốn sách này.
200
CHƯƠNG
10
KHÔI PHỤC ẢNH
10.1 Chỉ dẫn
Trong các chương trước chúng ta đã khảo sát các giả thiết để làm mất đi các
ảnh hưởng làm suy giảm chất lượng ảnh. Chúng bao gồm làm mất nhiễu xung
thông qua các bộ lọc đối xứng, tăng độ tương phản thông qua các công cụ như
sửa đổi lược đồ mức xám, lọc đồng hình, và lọc tĩnh Wallis. Trong các phần
này, chúng ta đã không xem xét nguyên nhân của sự suy giảm cũng như liệu
nó đã được thoả mãn hay chưa. Các nguyên nhân khác nhau, bao gồm cả các
vết mờ ảnh, đòi hỏi sự phát triển cho một kiểu khắc phục các sự suy giảm gọi
là hệ thống ảnh. Hệ thống ảnh có thể xây dựng trên khái niệm hàm tán xạ điểm
(Point-Spead-Funtion - PSF), ví dụ, tác động trên ảnh ghi lại của một điểm gốc
của độ sáng trên vật thể quan tâm. Biến đổi Fourier của PSF trở thành hàm
truyền đạt ánh sáng (Optical-Tranfer-Funtion - OTF).
Trong chương này ta sẽ quan tâm đến các nguyên nhân làm mất sự hội tụ
ảnh. Ba dạng của vết mờ cần được quan tâm là: (1) ảnh không rõ nét, (2) dạng
vết mờ chuyển động đồng dạng, (3) vết mờ do ảnh hưởng chiếu sáng lâu qua
khí quyển. Tất cả các nguyên nhân này gây ra các giá trị khác nhau của PSF
đòi hỏi ta phải giới hạn phạm vi các vết mờ.
10.2 Các PSF cho khác dạng khác nhau của các vết mờ
Nếu chúng ta coi rằng hệ thống ảnh là tuyến tính, thì ta có thể viết
ddyxihyxib),(),(),( (10.1)
ở đây ib(x,y) là ảnh mờ, h(x,y) là PSF, i(x,y) là ảnh nhập vào không bị suy
giảm. Bởi vì chúng ta đã được cho ib(x,y) và muốn phục hồi i(x,y) nên cần phải
đánh giá h(x,y). Nếu h(x,y) đã biết, thì vấn đề có thể giải quyết được và quá
trình đó được gọi là giải chập. Bởi vì biết rất ít về hệ thống mờ nên việc này
được gọi là giải chập mù. Nếu trong một số trường hợp bằng cách này hay
cách khác h đã được cho trước thì giải pháp được gọi là phương pháp tiên
nghiệm. Trong phần lớn các trường hợp còn lại thì h đều chưa biết, giải pháp
này thuộc loại phương pháp hậu nghiệm.
PSF cho ba kiểu vết mờ được cho dưới dạng phương án giải quyết được đề
cập đến ở phần dưới đây.
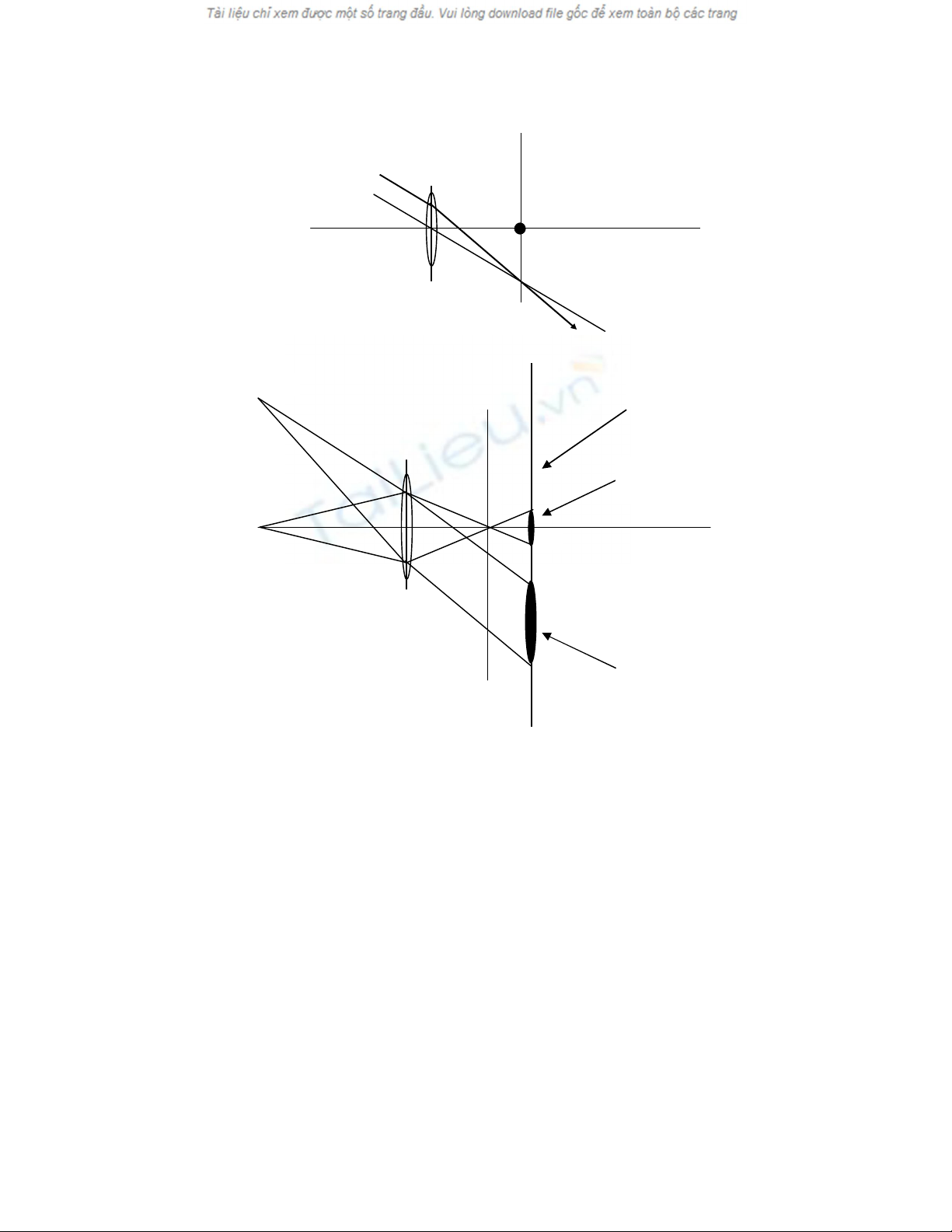
201
Hình 10.1 (a) Phương pháp tìm đư
ờng đi tia sáng.
(b) Sự tán xạ của điểm nằm trên và ngoài trục chính.
10.2.1 Tiêu điểm của thấu kính có dạng tròn
Hình 10.1b minh hoạ một hệ thống quang học đơn giản trong đó một điểm
gốc cho một hàm phân tán điểm do sự không chính xác của tiêu cự. Hình
10.1a giới thiệu cách xác định đường đi của tia sáng, làm sáng tỏ phương pháp
xác định ảnh trong hình 10.1b. Cách xác định đường đi của tia sáng từ một
điểm nằm ngoài trục theo các bước sau: Vẽ một tia bất kỳ đi qua điểm (1) gặp
thấu kính tại A. Vẽ mặt phẳng tiêu (thứ hai) của thấu kính. Vẽ tia (3) song song
với tia 1, đi qua tâm của thấu kính. Tất cả các tia như thế này gọi là tia chính.
Tia chính gặp mặt phẳng tia 2 tại B. Nối A và B sau đó kéo dài. Đây chính là
tia khúc xạ. Cho một điểm nằm trên quang trục tia sáng phải đi qua tiêu điểm
thứ hai. Dùng cách tìm đường đi của tia sáng qua thấu kính cho ta thấy hàm
tán xạ điểm của một điểm nằm trên quang trục rất khác so với hàm tán xạ của
một điểm nằm ngoài quang trục. Cũng cần chú ý rằng vật thể xa thấu kính sẽ
có tán xạ khác với vật thể gần thấu kính.
1 2
3
4
F2
A
B
(a)
I1
I2
F2
O2
O1
Màn chắn
ảnh của điểm
trên trục chính
ảnh của điểm
ngoài trục chính
202
Đạo hàm các PSF có dạng như một Gauss hai chiều:
)
2
exp(
2
1
),( 2
2
2

r
rG
(10.2)
ở đây là bán kính của vết mờ, r là khoảng cách bán kính kể từ tâm vết mờ.
10.2.2 Các vết mờ chuyển động đồng dạng
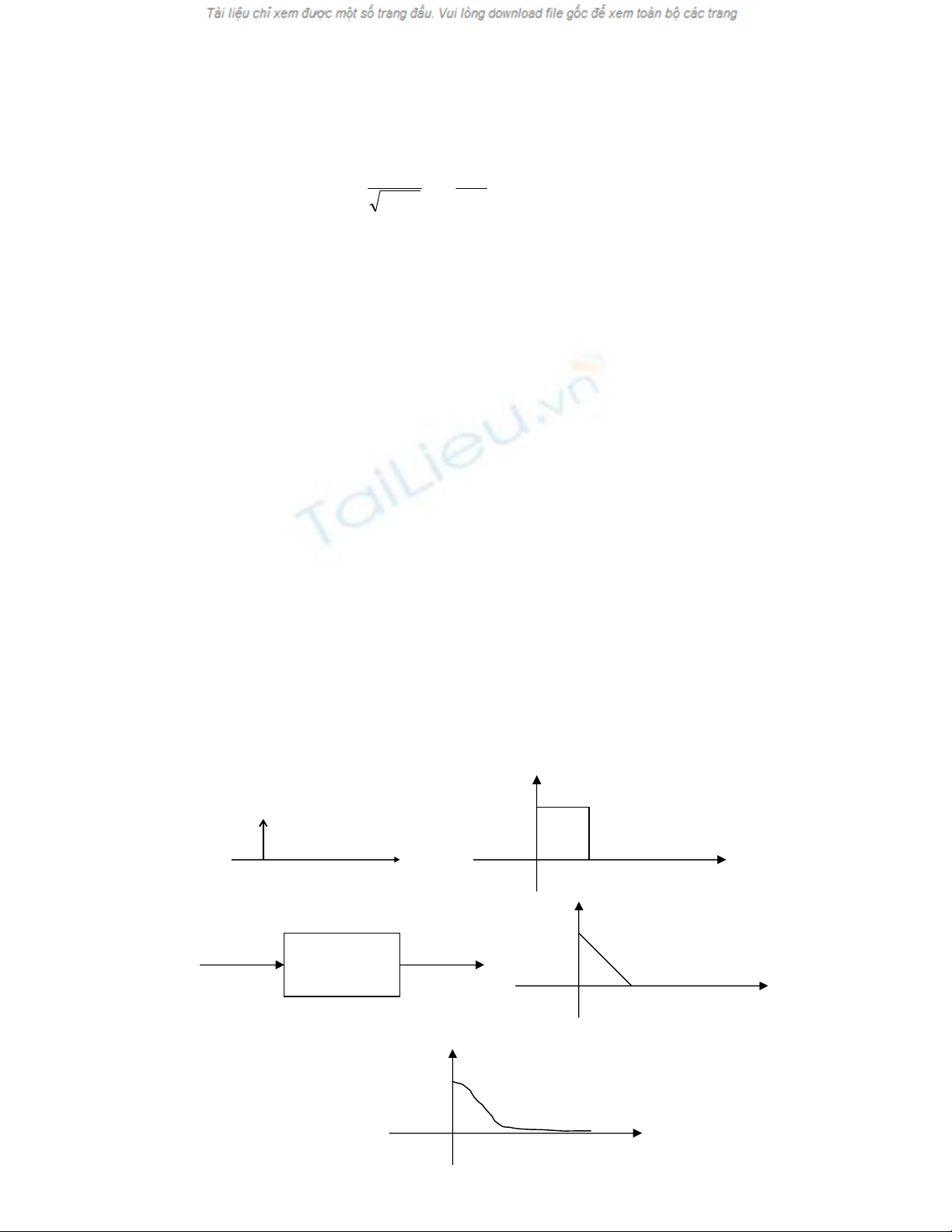
Vết mờ chuyển động là kết quả của quá trình chụp phim ảnh của một vật thể
chuyển động trong một thời gian đủ lớn để ghi lại hàng loạt các vị trí của vật
thể. Chú ý rằng nếu thời gian chiếu sáng quá nhỏ so với chuyển động của ảnh
thì vết mờ sẽ không cần quan tâm đến. Vết mờ chuyển động cũng có thể là kết
quả của chuyển động của camera. Ta có thể tạo ra vết mờ chuyển động bằng
cách trải rộng một đơn vị mẫu dọc theo hướng chuyển động (xem hình 10.2).
PSF có thể tạo ra bằng một hình vuông gạch chéo trong đường cong (a) của
hình 10.2 khi phim ghi lại một loạt các vị trí khác nhau vật thể với các thời
gian chiếu sáng khác nhau. Thời gian chiếu sáng lớn nhất được cho vị trí đầu
tiên khi cửa sập camera mở ra lần đầu tiên, thời gian chiếu sáng nhỏ nhất được
cho vị trí cuối cùng vật thể chiếm giữ trước khi của sập được hạ xuống. Điều
này giúp chúng ta lựa chọn hình tam giác hoặc là Gauss trong hình 10.2 như
những mô hình thực tế hơn cho vết mờ chuyển động.
10.2.3 Vết mờ do ảnh hưởng của khí quyển
Bình thường, hệ số khúc xạ của khí quyển là hằng số trong một vùng rộng
lớn. Trong một số trường hợp sự thay đổi của khí quyển có thể tạo ra một dãy
các hệ số khúc xạ khác nhau. Đây là nguyên nhân gây ra các vết mờ trên ảnh.
Ảnh của vật thể trong vũ trụ qua tầng khí quyển bao quanh trái đất là một ví
dụ. Nếu những vật thể này phải quan sát qua tầng khí quyển, với thời gian
chụp ảnh lâu, độ hoàn hảo của ảnh sẽ bị giới hạn.
h(x,y)
Mẫu đơn vị
O x
(a)
x
h(x,y)
h(x,y)
(b)
x
h(x,y)
(c)
x
203
Hình 10.2 Mô hình ảnh mờ do chuyển động.
Một PSF đã được sử dụng và kiểm tra qua thực nghiệm để mô hình hoá quá
trình này là:
6/52
3
2
2)(
1
),( yKxK
eKyxh
(10.3)
ở đây Ki là các hằng số. Để cho tiện lợi trong phân tích, 5/6 thường được thay
thế bởi tính đồng nhất để rút ra mô hình đáp ứng xung đường cong Gauss có
dạng
)
22
(2
2
2
2
),( yx
yx
Keyxh
(10.4)
ở đây K là hằng số khoảng cách biên độ, x và y là các hệ số phân tán vết mờ.
10.3 Đánh giá phạm vi vết mờ
Trong các bước phân tích tiếp theo chúng ta sẽ coi rằng mô hình cho hệ
thống ảnh mờ là tuyến tính bất biến, LSI, hoặc ít nhất có thể được xấp xỉ như
một hệ thống. Hệ thống quang học mà ta được biết là kính mắt có đặc điểm là
ảnh của vật nhìn qua kính sẽ có ít hoặc không có sự biến đổi nào. Cho các hệ
thống quang học khác bạn sẽ phải xem đây là một sự xấp xỉ và áp dụng một
PSF duy nhất lên toàn bộ ảnh, hoặc chia ảnh thành các miền nhỏ hơn và cho
tất cả các miền ta nhận được một PSF. Phép chia nhỏ trên ảnh này cho chúng
ta kết quả gần đúng tốt hơn, khi trên tất cả các miền nhỏ này chúng ta có thể
coi rằng PSF sẽ xấp xỉ với một hằng số phân tán tại tất cả các điểm. Dễ thấy
rằng hình 10.1 biểu diễn trường hợp hệ thống một thấu kính. Trong camera
người ta sử dụng nhiều thấu kính, và chúng được lắp ghép để làm rõ hơn
những cảnh mờ.Xem xét một đường biên dọc trong một ảnh không bị mờ với
độ lớn tại vị trí (x0,y0), được định nghĩa như sau:
x< x
x x
),(
0
0
nÕu
nÕu
k
k
yxi
nếu h(x,y) là PSF, thì ảnh mờ được cho bởi
ddiyxhyxib),(),(),( (10.5)