Hệ điều khiển nhúng với PETRI NET
I. Mở đầu.
Mô hình hóa là phương pháp xây dựng mô hình toán học của hệ thống bằng cách
phân tích hệ thống thành các khối chức năng, trong đó mô hình toán học của các
khối chức năng đã biết hoặc có thể rút ra được dựa vào các quy luật hóa lý. Mô
hình hệ thống được xây dựng dựa trên cơ sở liên kết các khối chức năng.
Trên cơ sở mô hình hóa có thể kiểm tra, đánh giá kết quả xem hệ thống có phù hợp
với yêu cầu hay không. Nên mô hình hóa hệ thống giúp đánh giá tính thực tiễn của
các công việc định làm, từ đó đưa ra phương án lựa chọn tốt nhất dành cho hệ
thống. Để mô hình hóa hệ thống có thể sử dụng rất nhiều hướng khác nhau như:
hướng cấu trúc, hướng dữ liệu, hướng đối tượng, Petri Net (lưới Petri Net)..v.v.
Trong đó, Petri Net là ngôn ngữ mô hình hóa dùng để đặc tả các hệ thống phân tán
rời rạc. Petri Net được phát minh vào năm 1962 bởi Carl Adam Petri nhằm mục
đích mô tả các quá trình hóa học. Ngày nay, Petri Net đã được phát triển rất mạnh
mẽ, đã được ứng dụng rất rộng rãi trong rất nhiều lĩnh vực khác nhau như: sinh
học, hóa học, môi trường, kỹ thuật, truyền thông, điều khiển, hệ thống sản xuất,
robot [1],[2]..v.v.. Trong nội dung bài báo này chúng tôi sẽ giới thiệu Petri Net cơ
bản và sử dụng nó để mô hình hóa các hệ điều khiển nhúng cụ thể là hệ thống nhà
thông minh.
II. Petri Net
Petri Net còn được gọi là
Place/Transitions Networks (mạng
vị trí/chuyển tiếp) và được hiển thị
bằng đồ thị có hướng gồm có 2 loại
node:
* Transition (chuyển tiếp) có dạng
hình chữ nhật hoặc hình vuông -
biểu diễn các sự kiện rời rạc có thể
xảy ra.
* Place (vị trí) có dạng hình tròn -
biểu diễn trạng thái các điều kiện.
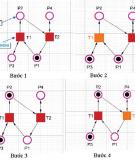
Ví dụ minh họa ở Hình 1, Petri Net có 4 place, 2 transition.
Các place và transistion được nối với nhau bằng các đường nối (liên kết). Chỉ có
thể nối place với transition, không thể nối giữa hai place hoặc hai transition với
nhau. Khi một đường nối đi từ một place đến một transition, thì place đó được gọi
là input place của transition đó. Ngược lại, khi có một đường nối đi từ transition tới
một place thì place đó được gọi là output place của transition đó. Các place có thể
chứa một số lượng các token (thẻ) nào đó. Token trong place được biểu diễn bằng
dấu chấm.
Transition của Petri Net có thể hoạt động được khi tất cả các input place của nó có
ít nhất một token. Sau khi transition hoạt động (bắn), mỗi input place sẽ mất một
token và mỗi output place thêm một token. Trong Hình 1, bước 1, place P1 ở trạng
Hình 1. Ví d
ụ minh họa về Petri Net
thái chứa token tuy nhiên transistion T1 không thể hoạt động và không cho phép
token đi qua. Transition T1 yêu cầu cả place P3 và P1 chứa token thì nó mới hoạt
động. Bước 2 minh họa những gì sẽ xảy ra khi place P1 và P2 có chứa token do đó
T1 có thể hoạt động và cho phép một token chuyển đến place khác, trong trường
hợp này là P2. Bước 3 là kết quả từ bước 2 sau khi T1 hoạt động. Token đã được
chuyển từ place P1 và P3. Place P1 bị mất token vì từ P1 có đường nối một chiều
(input place). Place P3 có đường nối hai chiều (vừa là input place và vừa là output
place) tới T1 vì vậy P3 đã không bị
mất token của mình qua transition
T1.
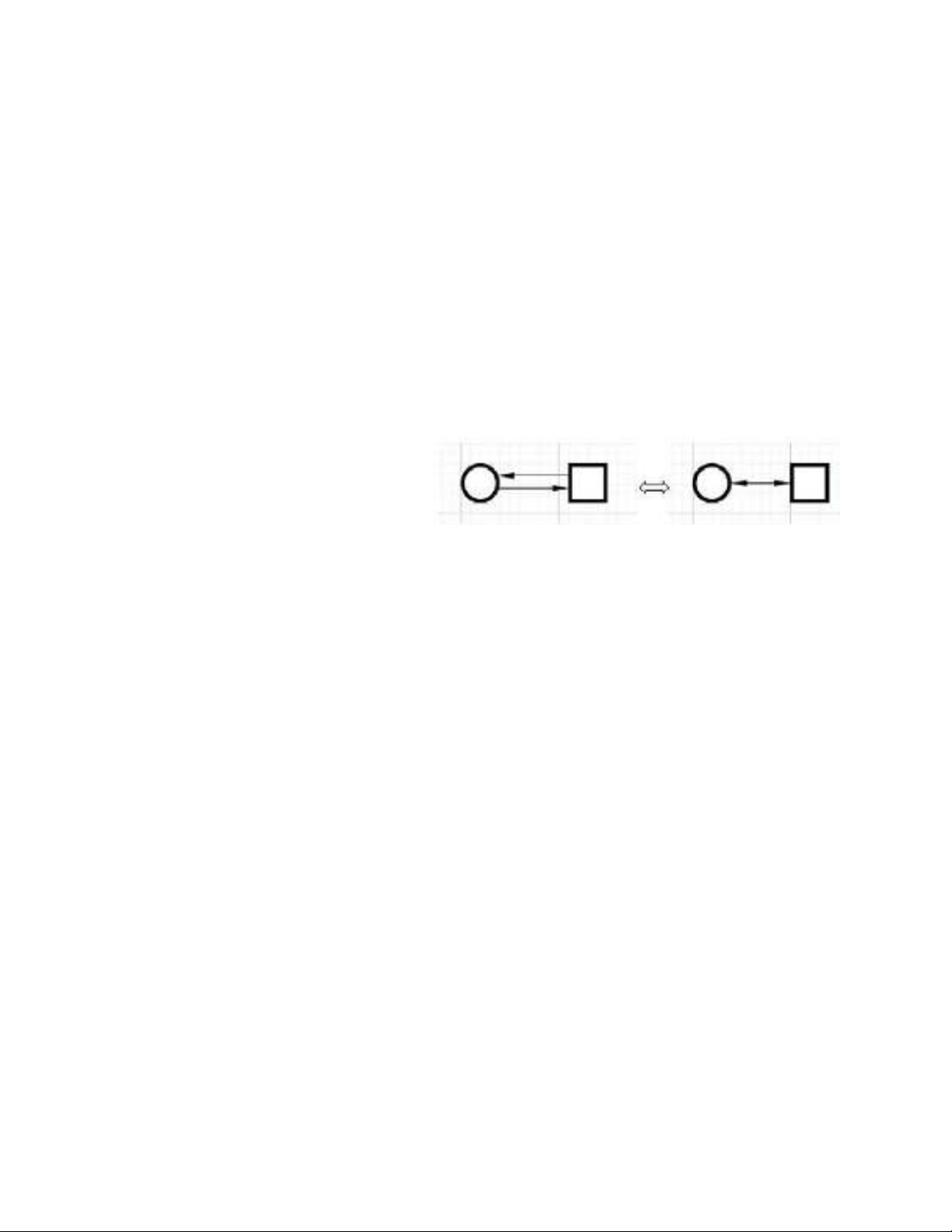
Đường nối hai hướng trong thực tế
là hai đường nối một chiều theo hai
chiều ngược nhau như minh họa trên Hình 2.
Ở bước 4 Hình 1 là quá trình giống với bước 2 khi cả place P2 và P4 chứa token
(đang hoạt động) do đó transition T2 có thể hoạt động và cho phép các token vượt
qua tới place P1 .
Tại một thời điểm, việc phân bố các token trên các place, được gọi là đánh dấu
(marking) của Petri Net. Nó biểu diễn trạng thái hiện tại của hệ thống được mô
hình hóa. Một marking của Petri Net với m place được biểu diễn bởi vector M (m
x1), trong đó các thành phần của vector là không âm, ký hiệu là M(p), biểu diễn
cho số token ở các place P tương ứng [3]. Trong mô hình Petri Net biểu diễn ở
bước 1, Hình 1 thì:
M = (1,0, 0, 0)T
Một cách hình thức, một Petri Net có thể được định nghĩa như sau:
Hình
2
.
Biểu diễn đường nối hai hướng
PN = (P, T, I, O, M0)
Trong đó:
1. P = {p1, p2…pm} là tập hữu hạn các place.
2. T = {t1,t2,…tn} là tập hữu hạn của transition.
.T=, PTP và T là 2 tập tách rời nhau : P
N là hàm xác định hướng3. I: (P x T) đường nối từ các input place tới các
transition, trong đó N là một tập hợp các số nguyên (là 0 hoặc 1). Trong trường
hợp tổng quát nó là các số nguyên không âm.
N là hàm xác định hướng đường nối từ các transition tới các output place.4. O:
(P x T)
N trạng thái (marking) ban đầu.5. M0: P
Ví dụ, Petri Net trên Hình 1 với trạng thái ban đầu là bước 1 được biểu diễn với
các thành phần như sau:
PN = (P, T, I, O, M0)
1. P = {P1,P2,P3,P4}
2. T = {T1,T2}
3. Input place
4. Output place