Hướng dẫn giải đề thi Đại học khối A môn Toán 2013
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 1 -
HƯỚNG DẪN GIẢI ĐỀ THI ĐẠI HỌC THPT NĂM 2013
MÔN TOÁN HỌC
Câu 1.
32
3 3 1y x x mx
a. Khi m = 0 ta có hàm số:
32
3 1( )y x x C
TXD: D = R
'2
'
36
0
02
y x x
x
yx
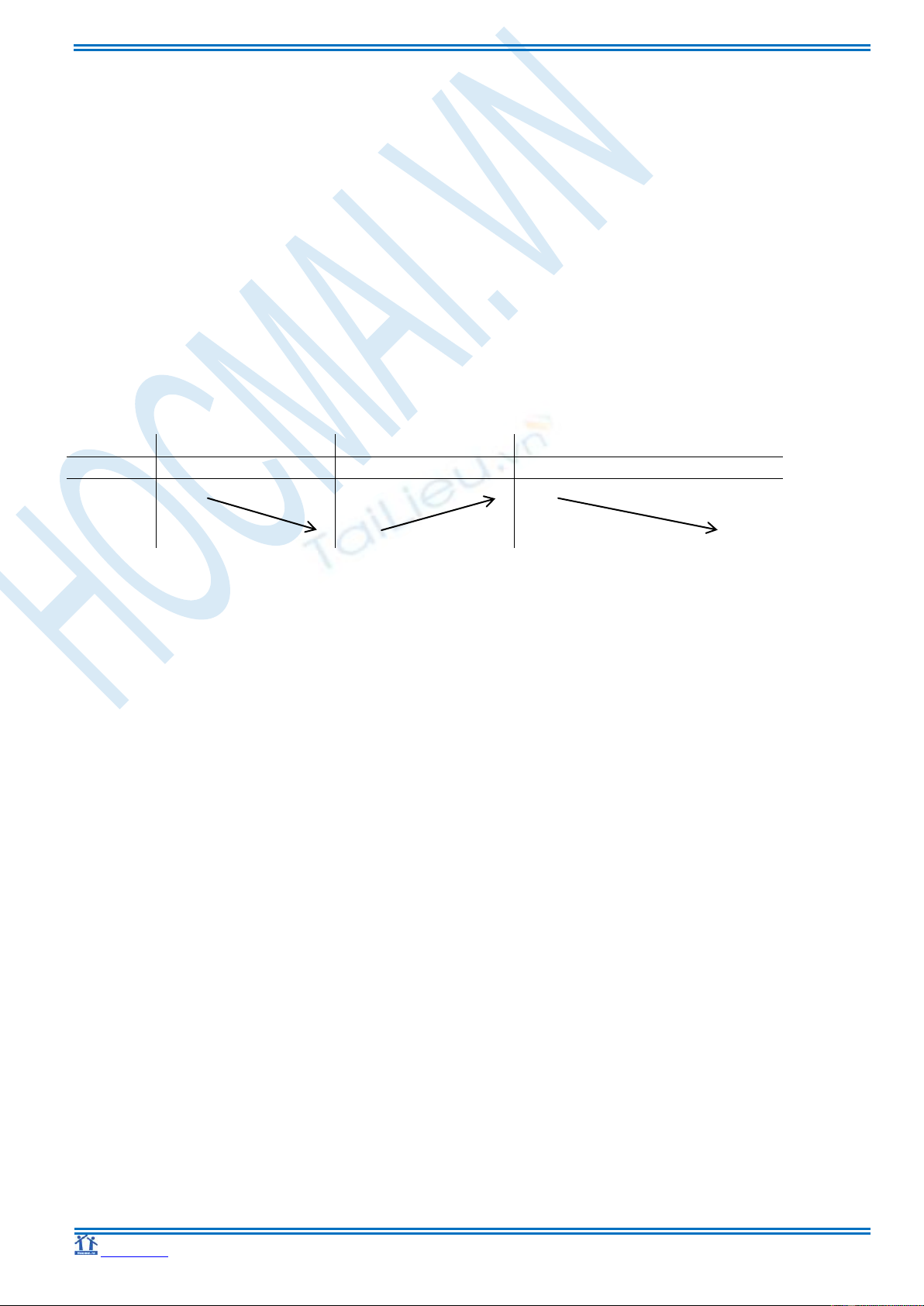
* Bảng biến thiên
x
-
0
2 +
y’
-
0 +
0 -
y
+
-1
3
-
+ Hàm số nghịch biến trên mỗi khoảng
,0 ; 2;
+ Hàm số đồng biến trên (0, 2)
* Cực trị:
Hàm số đạt cực đại tại
23
CD CD
xy
Hàm số đạt cực tiểu tại
01
CT CT
xy
* Đồ thị hàm số:
''
''
66
0 1 (1) 1
yx
y x y
Suy ra điểm uốn U (1, 1)
+ (C) giao với trục Oy: (0; -1)
Điểm cực đại: (2; 3)
Điểm cực tiểu: (0; -1)

Hướng dẫn giải đề thi Đại học khối A môn Toán 2013
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 2 -
b.
32
22
3 3 1 (1)
' 3 6 3 3( 2 )
y x x mx
y x x m x x m
Để hàm số (1) nghịch biến trên
0;
thì
'0y
trên
0;
hay :
2
2
2 0 (0; )
2 (0; ) (*)
x x m x
m x x x
Xét
2
( ) 2g x x x
trên
0;
'( ) 2 2
'( ) 0 1
g x x
g x x
Bảng biến thiên:
x
0
1
g'(x)
-
0 +
g(x)
-1
(*) Xảy ra khi
(0; )
min ( ) 1
x
m g x
Kết luận
1m
Câu 2:
1 + tanx =
2 2sin( ) (1)
4
x
ĐKXĐ: cosx
0.
(1) 1+
sinx
cos x
2 2sin( )
4
x
(sinx + cosx) =
2 2.cos .sin( )
4
xx
2
sin( )
4
x
=
2 2.cos .sin( )
4
xx

Hướng dẫn giải đề thi Đại học khối A môn Toán 2013
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 3 -
sin( )
4
x
[1-2 cosx]=0
sin( ) 0 44
4
122
cos 33
2
x k x k
x
x k x k
x
Kết hợp điều kiện cosx
0
thấy các nghiệm đều thỏa mãn.
Kết luận: nghiệm của phương trình là:
4
xk
;
2
3
xk
Câu 4
22
2
1
2 2 2
22
1 1 1
22
1
11
2 2 2
222
1 1 1
12
1ln
11
(1 )ln ln ( )ln
2 2 2
ln ln ln 2ln 2 1
1 1 1
2
1 1 ln 1
( )ln ln ( ) 1
2
ln 2 1 ln 2 1
()
1
22
53
ln 2
22
x
I xdx
x
xdx xdx xdx
xx
x
I xdx x x dx x x x
x
x
I xdx xd dx
x x x x
x
I I I
Câu 5.

Hướng dẫn giải đề thi Đại học khối A môn Toán 2013
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 4 -
Tính
SABC
V
Gọi H là trung điểm của BC. Suy ra SH vuông góc với BC
Vì
( ) ( )
( ) ( )
()
SBC ABC
SBC ABC BC
SH BC SH ABC
Tam giác SBC đều cạnh = a suy ra SH =
3
2
a
Tam giác ABC vuông góc tại A, góc ABC =
0
30
, BC = a suy ra AB =
03
. os30 2
a
BC c
Và AC =
2
a
Suy ra
3
1 1 1 1 3 3
. . . . . . ( )
3 3 2 6 2 2 2 16
SABC ABC
a a a a
V SH S SH AB AC dvtt
Tính khoảng cách từ C đến (SAB)
Ta có: AH =
22
BC a
Tam giác SAH vuông tại H suy ra
22
22
3
44
aa
SA SH AH a
Tam giác SHB vuông tại H suy ra
22
22
3
44
aa
SB SH HB a

Hướng dẫn giải đề thi Đại học khối A môn Toán 2013
Hocmai.vn – Ngôi trường chung của học trò Việt
Tổng đài tư vấn: 1900 58-58-12
- Trang | 5 -
Suy ra tam giác SHB cân tại S. Gọi M là trung điểm của AB suy ra SM =
22
2 2 2 2
3 3 13
4 16 4
aa a a
SB BM a a
Suy ra diện tích tam giác
2
1 1 13 13 39
. . ( )
2 2 4 2 16
SAB
a a a
S SM AB dvdt
Ta có
3
..
1( ,( )).
3 16
S ABC C SAB SAB
a
V V d C SAB S
3
3
2
33 16 3 39
16
( ,( )) .
16 13
39 39
SAB
aa a a
d C SAB Sa
Câu 8a.
6 1 2
:3 2 1
x y z
Mặt phẳng (P) đi qua A và vuông góc với
Mặt phẳng (P) có vtpt :
//
p
nu
= (-3; -2; -1)
Phương trình mặt phẳng (P): -3(x – 1) – 2(y-7) + 1(z-3) = 0
-3x – 2y + z +14 = 0
M ∈
63
12
2
xt
M y t
zt
2 30AM
AM2 = 120
2
14 8 6 0tt
1 (3; 3; 1)
3 51 1 17
( ; ; )
7 7 7 7
tM
tM
Câu 8b..
Mặt cầu (S) có tâm I (1;-2;1) bán kính
14R
2 2 2
2.1 3.( 2) 1.1 11 14
; 14
14
2 3 1
d I P R
Mặt phẳng (P) tiếp xúc với (S).
Lập phương trình đường thẳng d đi qua I (1;-2;1) và
()mp P
Ta có véc tơ chỉ phương
d
u
//
d
u
12xt
23yt
1zt
tR
Tọa độ tiếp điểm mà M là giao của d và (S);
()MP
2 2 2
1 2 2 3 1 2 1 2 4 2 3 2 1 8 0t t t t t t


























