1
Kỹ Thuật Số
Kỹ Thuật Số
2
Ch ng 2ươ
Các c ng logic c b n ổ ơ ả
và đ i s Booleạ ố
3
Các phép toán logic c b nơ ả
Các c ng logic c b nổ ơ ả
Các đ c tính c b n c a h th ng s đ m nh phânặ ơ ả ủ ệ ố ố ế ị
Th c hi n các m ch logic s d ng các c ng c b nự ệ ạ ử ụ ổ ơ ả
S d ng đ nh lu t DeMorgan đ đ n gi n hóa các bi u ử ụ ị ậ ể ơ ả ể
th c logic.ứ
Các ph ng pháp bi u di n hàm Booleươ ể ễ
Các ph ng pháp rút g n hàm Booleươ ọ
4
2.1
2.1 Bi n và h ng trong đ i s Booleế ằ ạ ố
Bi n và h ng trong đ i s Booleế ằ ạ ố
Bi n và h ng trong đ i s Boole ch nh n m t trong hai giá tr ế ằ ạ ố ỉ ậ ộ ị
là 0 ho c 1.ặ
Các bi n Boole (hay bi n logic) th ng đ c s d ng đ bi u ế ế ườ ượ ử ụ ể ể
di n m c đi n áp trên m t dây d n hay t i các c c vào/ra c a ễ ứ ệ ộ ẫ ạ ự ủ
m ch.ạ
Các giá tr 0 và 1 không ph i là các con s th c mà ch bi u ị ả ố ự ỉ ể
di n m t m c đi n áp, đ c g i là m c logic.ễ ộ ứ ệ ượ ọ ứ
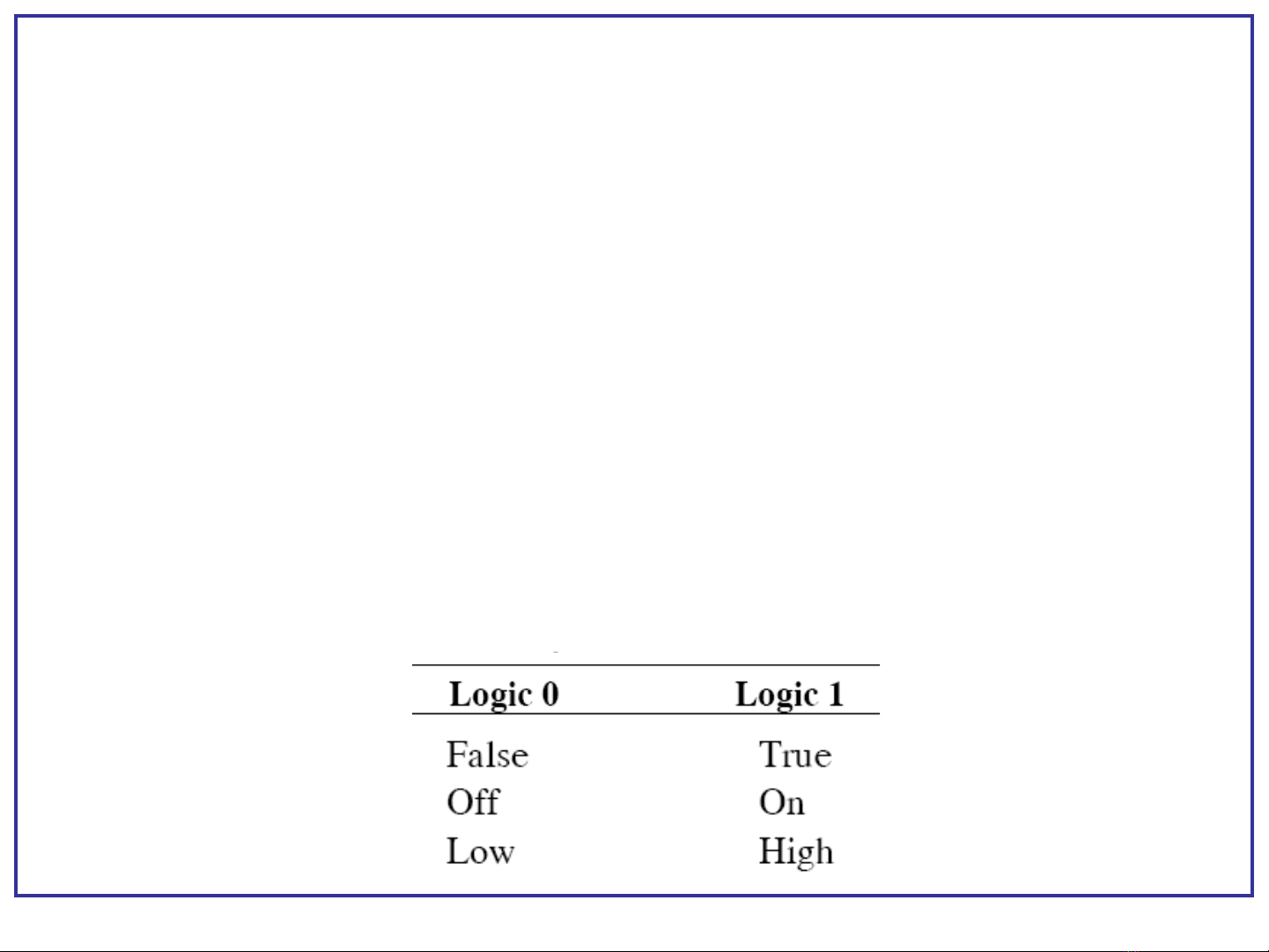
M t s ký hi u khác cũng đ c s d ng đ bi u di n hai m c ộ ố ệ ượ ử ụ ể ể ễ ứ
logic thay cho các con s 0 và 1ố
5
Phép c ng logic: ký hi u là OR, (+)ộ ệ
Phép nhân logic: ký hi u là AND, (.)ệ
Phép bù/đ o logic: ký hi u là NOT, ( ), ( ’ )ả ệ
Các phép toán cơ bản trong đại số Boole
Các phép toán cơ bản trong đại số Boole
2.1
2.1 Bi n và h ng trong đ i s Booleế ằ ạ ố
Bi n và h ng trong đ i s Booleế ằ ạ ố