BÀI TẬP SỐ 3
Mục tiêu: Làm quen với các khái niệm và cách tính hàm độ lớn xác suất, hàm phân phối
tích lũy, kỳ vọng, phương sai của:
Biến ngẫu nhiên X rời rạc
Biến X có phân phối đều rời rạc
Biến X có phân phối nhị thức
Biến X có phân phối chuẩn
Tóm tắt lý thuyết:
Biến ngẫu nhiên rời rạc X:
Hàm độ lớn xác suất (pdf): Pr(X), f(X)
Hàm phân phối tích lũy (cdf): ( ) ( ) ∑ ( )
Kỳ vọng: ( ) ∑ ( )
Phương sai: ( ) ∑( ) ( )
( )
Chứng minh:
( ) ∑( ) ( ) ∑( ) ( ) ∑ ( )
∑ ( )
∑ ( ) ∑ ( )
∑ ( )
( )-
Độ lệch chuẩn: √ ( ) ( )
Phân phối xác suất của X: là tất cả các giá trị x mà X có thể nhận và xác suất Pr(x)
tương ứng của chúng. Bảng phân phối xác suất:
X
Pr(X=x)
Phân phối đều rời rạc:
Biến X có phân phối đều rời rạc nếu nó thỏa hai điều kiện sau:
▫ X có thể nhận các giá trị nguyên trong đoạn [a, b].
▫ Các giá trị mà X có thể nhận có xác suất bằng nhau.
X có phân phối đều rời rạc trong đoạn [a,b] thì:
Hàm độ lớn xác suất:
).(,
1
1
)Pr( bxa
ab
x
Hàm phân phối tích lũy:
Kỳ vọng:
Phương sai:
Phân phối nhị thức:
Biến X có phân phối nhị thức nếu nó thỏa các điều kiện sau:
▫ Số lần thí nghiệm của tiến trình ngẫu nhiên đang xét là cố định
▫ Hậu quả của thí nghiệm chỉ có thể được phân thành 2 lớp (thành công hay thất
bại)
▫ Xác suất thành công trong mọi lần thí nghiệm là như nhau
▫ Các lần thí nghiệm là độc lập nhau
▫ X = số lần thí nghiệm thành công trong n lần thí nghiệm
X có phân phối nhị thức với số lần thí nghiệm là n, xác suất thành công trong mỗi thí
nghiệm là p thì:
Hàm độ lớn xác suất: ( ) (
) ( )
Hàm phân phối tích lũy: ( ) ∑ ( )
Kỳ vọng: E(X) = np
Phương sai: V(X) = np(1-p)
Phân phối chuẩn:
.
,1
,
1
1
,0
)(
bx
bxa
ab
ax
ax
xF
2
ab
.
12
))(2(
)(
2abab
XV
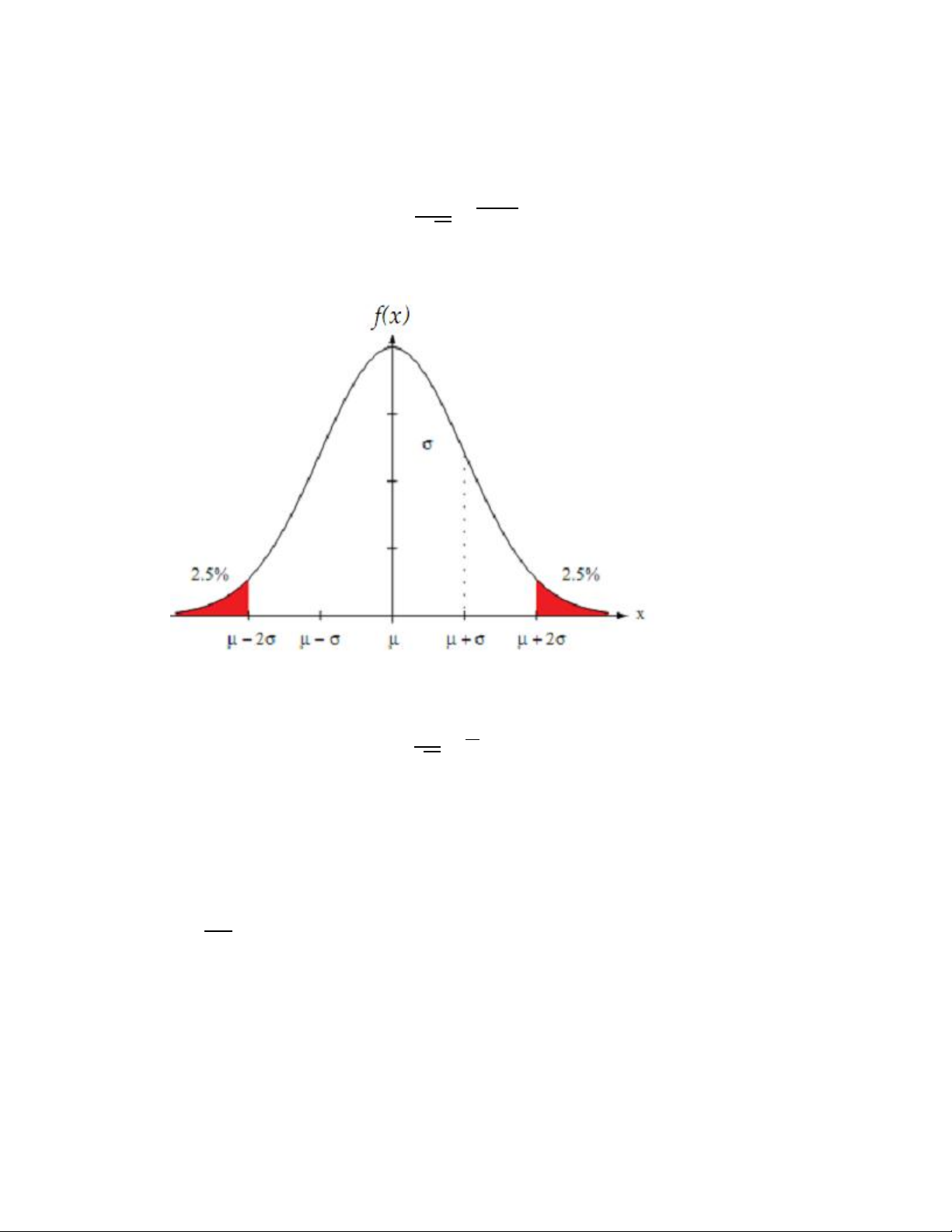
Phân phối chuẩn là mô hình xác suất được đặc trưng bởi trung bình (μ) và phương sai
(σ2). Ký hiệu là: N(μ, σ2) hay N(μ, σ)
Hàm mật độ xác suất: ( )
√ ( )
Hình dạng: hình chuông, khác nhau ở tâm và độ rộng
Phân phối z (phân phối chuẩn chính tắc): là phân phối chuẩn với μ=0, σ2=1
Hàm mật độ xác suất: ( )
√
Điểm chuẩn (điểm z): là giá trị biểu diễn độ lệch chuẩn trên hay dưới trung bình.
Bảng phân phối z: bảng tra giá trị hàm phân phối tích lũy khi biết giá trị z.
Chuẩn hóa phân phối chuẩn N(μ, σ) về phân phối z:
( ) ( )
Bài toán tính xác suất: Cho khoảng giá trị của x, tính Pr(x)
Bước 1: Vẽ hình của phân phối
Bước 2: Đưa về bài toán tính Pr(X<b)
Bước 3: Chuẩn hóa về phân phối Z: Pr(X<b) = Pr(z<a) với a có dạng gồm 2 chữ số
thập phân a = a1.a2a3
Bước 4: Tra bảng phân phối Z
Cách tra bảng phân phối Z:
Dòng: a1.a2
Cột: 0.0a3
Ví dụ: nếu a = 0.31 thì tìm dòng 0.3 và cột 0.01.
Bước 5: Kết luận
Bài toán tìm ngưỡng: cho Pr(X<a) hay Pr(X>a), tìm a.
Bước 1: chuyển về bài toán dạng cho Pr(X<a), tìm a
Bước 2: Tìm ô có giá trị gần Pr(X<a) nhất. Giả sử ô đó là ô ở dòng a1.a2, cột a3
Bước 3: Lấy dòng và cột cộng lại được số z có 2 chữ số thập phân.
Bước 4: Chuyển z về x theo công thức chuẩn hóa: x = zσ + μ
Bước 5: Kết luận
Xấp xỉ nhị thức bằng phân phối chuẩn
Bước 1: Kiểm tra n
Phân phối chuẩn có thể được dùng để xấp xỉ xác suất nhị thức khi số phép thử (n)
lớn, nghĩa là khi n thỏa (n×p) > 5 và (n × (1-p)) > 5.
Bước 2: Chuẩn hóa
Chuẩn hóa X (có phân phối nhị thức với n lớn) về phân phối chuẩn với trung bình và
phương sai: μ = E(X) = n×p, σ2 = var(X) = n×p×(1-p)
Bước 3: Hiệu chỉnh liên tục khi tính Pr(X) dựa vào phân phối chuẩn đã xấp xỉ
Vì phân phối nhị thức là phân phối rời rạc, còn phân phối chuẩn là liên tục, cần hiệu
chỉnh liên tục:
Bước 3a: Đưa về bài toán dạng xác suất Pr(X<a), hoặc Pr(X≤a) hoặc Pr(X>a) hoặc
Pr(X≥a) hoặc Pr(X=a)
Bước 3b: Xác định điểm cắt: là a
Bước 3c: Hiệu chỉnh
Nếu X≤a : a’ = a + ½ Pr(X≤a) = Pr(X≤a+1/2)
Nếu X≥a: a’ = a-1/2 Pr(X≥a) = Pr(X≥a-1/2)
Nếu X = a: a’ = a + ½, a’’ = a-1/2 Pr(X=a) = Pr(a-1/2≤X≤a+1/2)
Bước 4: Tính xác suất
Tính xác suất với giá trị đã hiệu chỉnh: Pr(X<a’), hoặc Pr(X≤a’) hoặc Pr(X>a’) hoặc
Pr(X≥a’) hoặc Pr(X=a’)
BÀI TẬP VỀ BIẾN NGẪU NHIÊN RỜI RẠC VÀ PHÂN PHỐI XÁC SUẤT
Bài tập mẫu:
Biến ngẫu nhiên X có phân phối xác suất
1
2
3
4
5
Pr(X=x)
0,5
0,1
0,2
0,1
0,1
a) Xác định hàm phân phối tích lũy F(X). Vẽ đồ thị (X,F(X))
b) Tính Pr[1≤X≤3,27] sử dụng:
i) Hàm độ lớn xác suất (pmf)
ii) Hàm phân phối tích lũy (cdf)
Giải:
a) Hàm phân phối tích lũy của biến ngẫu nhiên rời rạc
( ) ( ) ∑ ( )
Nên:
F(1) = Pr(X≤1) = Pr(1) = 0,5