Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
410
MÔ HÌNH GIẢI TÍCH TÍNH TOÁN NƯỚC DỀNH
TẠI KHU VỰC CỬA SÔNG
Nguyễn Xuân Tính1, Hitoshi Tanaka2
1Đại học Thủy lợi
2Đại học Tohoku, Sendai City, Japan
1. GIỚI THIỆU CHUNG
Các thông tin về mực nước cao thiết kế,
bao gồm cả chiều cao nước dềnh do sóng,
tại khu vực cửa sông vào là rất quan trọng
trong việc mô phỏng thay đổi hình thái cửa
sông, giao thông vận tải trên biển, và thiết
kế các công trình chỉnh trị sông. Nước dềnh
tại cửa sông là mực nước dâng cao hơn so
với mực nước tĩnh (SWL) do sóng vỡ gây ra
và thường xảy ra trong các điều kiện cực trị
như bão. Trong nghiên cứu này các dữ liệu
đo đạc từ các cửa sông ở Nhật Bản đã được
thu thập và phân tích (Tinh et al. 2009).
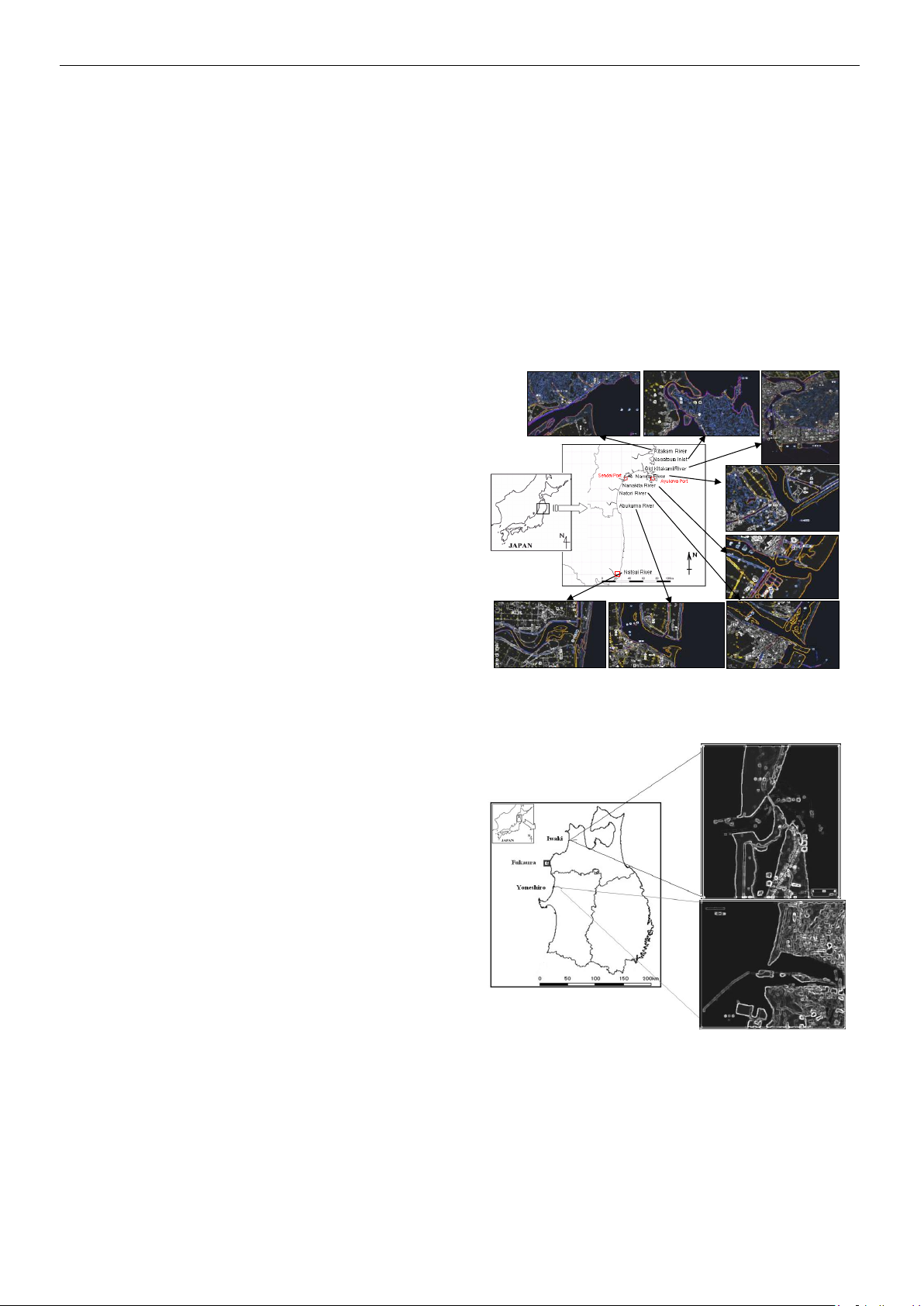
Hình 1 và hình 2 thể hiện vị trí của các cửa
sông chảy về phía biển Thái Bình Dương và
chảy về biển Nhật Bản. Quá trình dâng mực
nước tại khu vực cửa sông trong các cơn
bão có thể được gây ra bởi chênh lệch
trường áp suất, tốc độ gió và lưu lượng dòng
chảy sông. Do vậy, để loại bỏ các hiệu ứng
này trong nghiên cứu nước dềnh thì người ta
thường tiến hành đo đạc đồng bộ quá trình
thay đổi mực nước tại cửa sông và mực
nước triều khu vực lân cận có khoảng cách
đủ ngắn để trường áp suất không thay đổi
nhiều. Các kết quả phân tích thực nghiệm
này sau đó dùng để hiệu chỉnh và kiểm định
mô hình giải tích tính toán nước dềnh tại
khu vực cửa sông. Kết quả của mô hình giải
tích này rất hữu dụng cho các nhà quản lý
cũng như các kỹ sư trong việc thiết kế các
công trình tại khu vực cửa sông cũng như
cho việc nghiên cứu mô phỏng biến đổi hình
thái cửa sông được đầy đủ hơn.
Onahama
Port
Hình 1: Vị trí các cửa sông chảy ra biển
Thái Bình Dương
Hình 2: Vị trí các cửa sông chảy ra biển
Nhật Bản
2. PHƯƠNG PHÁP NGHIÊN CỨU
Tác giả sử dụng các phương pháp nghiên
cứu sau: Phương pháp phân tích thống kê;
phương pháp kế thừa các kết quả nghiên cứu
đã có sau đó phát triển mô hình giải tích mới;
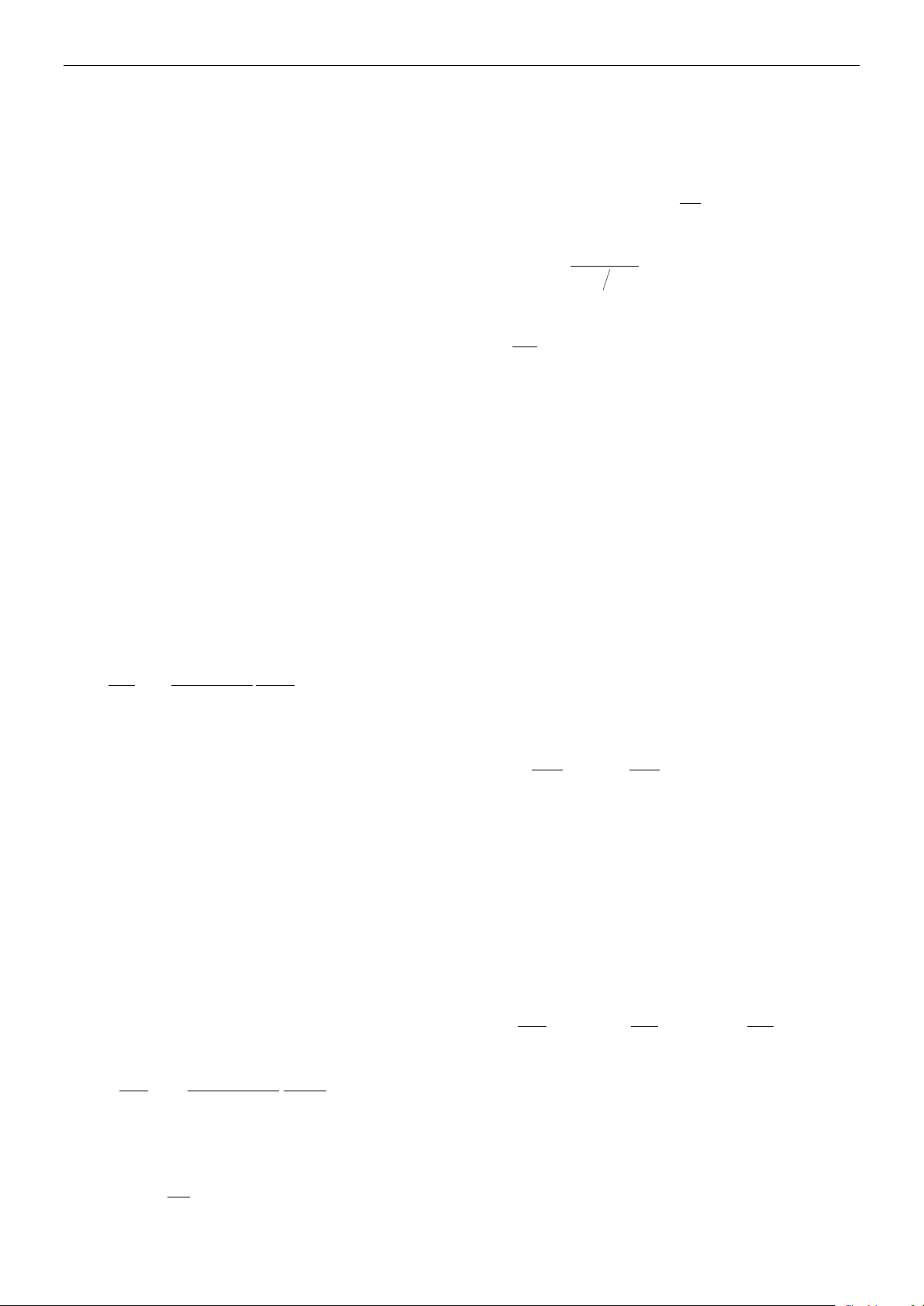
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
411
phương pháp khảo sát, điều tra và đo đạc
thực địa vùng nghiên cứu.
3. KẾT QUẢ NGHIÊN CỨU
Có nhiều công trình đã nghiên cứu để tính
toán hiện tượng nước dềnh và nước hạ do
sóng vỡ gây ra nhưng chủ yếu là tập trung ở
vùng bãi biển, nghiên cứu nước dềnh tại khu
vực cửa sông là tương đối ít do khó khăn về
mặt đo đạc số liệu và tương tác giữa sóng với
dòng chảy sông. Lý thuyết cơ bản đã được đề
xuất bởi Longuet-Higgins và Stewart (1963)
cho thấy các thành phần ứng suất bức do
sóng đóng một vai trò trong việc gây ra nước
dềnh hay nước rút trên một bãi biển dốc.
Bowen et al. (1968) đã tiến hành đo đạc chi
tiết nước dềnh và nước rút trong phòng thí
nghiệm và kết quả một lần nữa khẳng định
tính đúng đắn của lý thuyết đưa ra bởi
Longuet-Higgins và Stewart. Phương trình
động lực chính cho nước dềnh và nước rút
trên một bờ biển dốc theo hướng x có dạng
đơn giản hóa như sau;
bw
xx
dx
dS
hgdx
d
)(1
(1)
Ở đây,
là biến thiên của mực nước trung
bình và mực nước tĩnh dưới tác động của sóng,
xx
S
là ứng suất bức xạ do sóng, h là độ sâu cục
bộ, g là gia tốc trọng trường,
là mật độ nước,
w
và
là ứng suất ma sát tại mặt và tại đáy,
tuy nhiên hai thành phần này thường được bỏ
qua trong các nghiên cứu về nước dềnh.
Trong trạng thái ổn định, thông lượng
động học theo hướng vuông góc với bờ phải
phụ thuộc vào x. Khi độ cáo sóng giảm do
hiệu ứng sóng vỡ thì ứng suất bức xạ
xx
S
cũng giảm. Phương trình cân bằng động học
(1) khi đó trở thành;
dx
dS
hgdx
dxx
)( 1
(2)
Trong đó:
2
16
3gHSxx
(3)
Thay phương trình (3) vào phương trình
(2) rồi lấy tích phân theo x chúng ta có
nghiệm giải tích cho
như sau:
bb hhhK 2
16
1
(4)
ở đây:
2
381 1
K
là hệ có thực nghiệm;
= 0.78 là chỉ số sóng vỡ theo lý thuyết;
b
bH
h
là độ sâu tại vị trí sóng vỡ;
b
H
là độ
cao sóng vỡ; h là độ sâu cục bộ và trong
nghiên cứu này chúng tôi giả thiết độ sâu cục
bộ h bằng với độ sâu trung bình tại cửa
sông
R
h
. Thay các giá trị này vào phương
trình (4) ta có:
Rb hH 19.0
(5)
Komar và Gaughan (1972) đã thu được
một công thức thực nghiệm dựa trên lý thuyết
sóng biên độ nhỏ cho chiều cao sóng vỡ như
là một hàm của độ dốc sóng khu vực nước
sâu. Sunamura (1983) đã tiếp tục phát triển
giả thiết này để tính thêm ảnh hưởng của độ
dốc bãi biển. Quan hệ này được viết như sau:
0.25
0.2
b0
00
HH
i
HL



(6)
ở đây:
i
là độ dốc bãi biển;
0
H
là độ cao sóng
ngoài khơi (m); và
0
L
là độ dài sóng ngoài
khơi (m).
Chia cả hai vế phương trình (5) cho
0
H
và
thế phương trình (6) vào chúng ta được
phương trình giải tích hoàn chỉnh cho nước
dềnh khu vực cửa sông như sau;
0
2.0
25.0
0
0
0
19.0 H
h
i
L
H
HR
(7)
Phương trình này được áp dụng cho các
bộ dữ liệu tại các cửa sông tại Nhật Bản với
giá trị độ dốc sóng thay đổi từ 0,04 tới 0,08.
Độ dốc đáy biển trong toàn bộ khu vực
nghiên cứu là xấp xỉ bằng 0,024. Kết quả so
sánh với số liệu thực đo nước dềnh trong
các cơn bão đã chỉ ra rằng mô hình giải tích
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
412
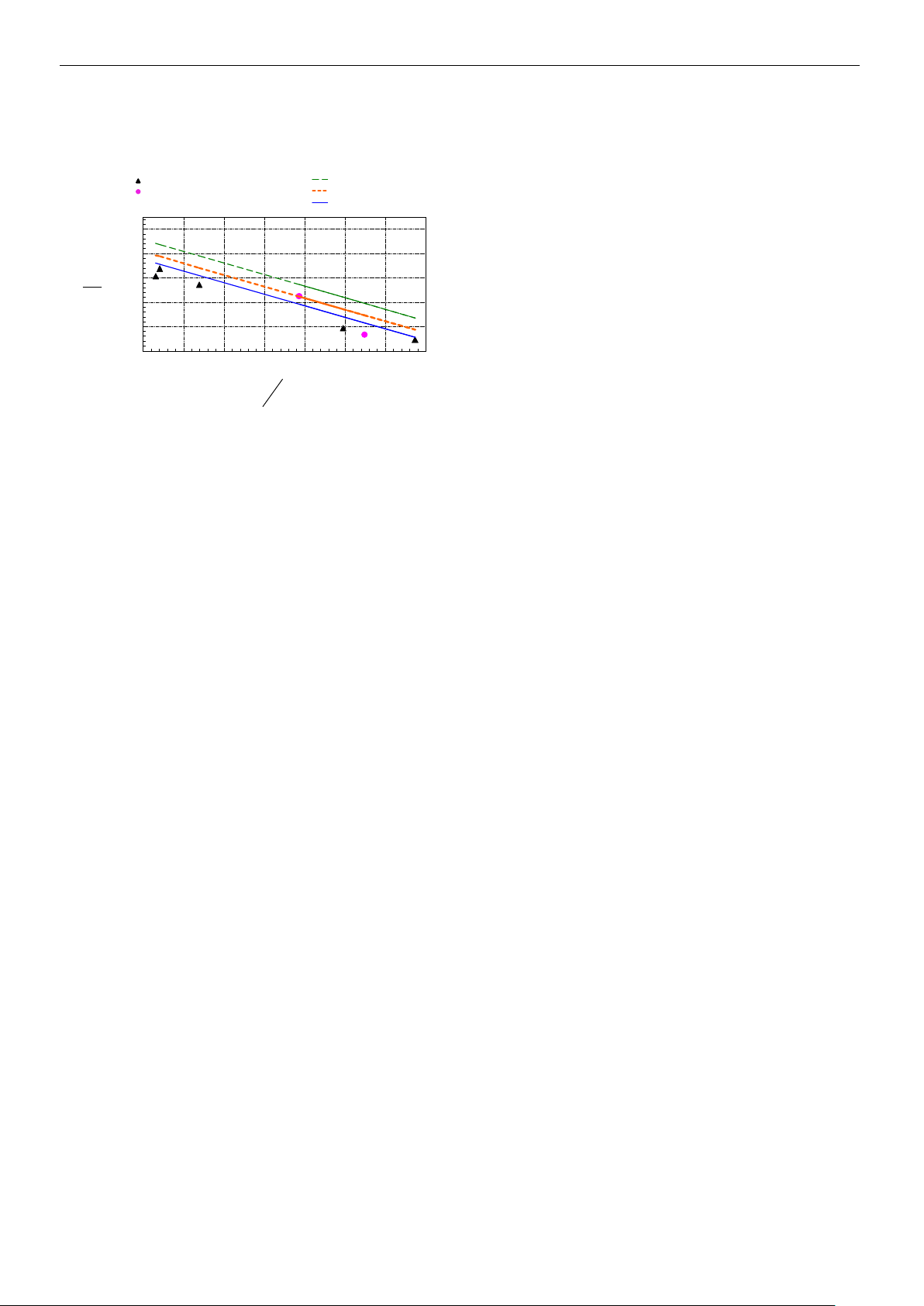
này cho kết quả khá phù hợp và có độ tin
cậy cao (hình 3).
0
0.04
0.08
0.12
0.16
0.2
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Facing the Pacific Ocean
Facing the Sea of Japan
Ho/Lo = 0.04
Ho/Lo = 0.06
Ho/Lo = 0.08
0
H
Empirical results
0
H
hR
Analytical results: Eq. (8), K= 0.19
Facing the Pacific Ocean
Facing the Pacific Ocean
Mô hình giải tích, khi K=0.19Số liệu thực đo
Sông phía Thái Bình Dương
Sông phía biển Nhật Bản
Hình 3: Kết quả so sánh mô hình giải tích
4. KẾT LUẬN
Kết quả tính phân tích thực nghiệm về
nước dềnh tại các khu vực cửa sông tại Nhật
cho thấy độ cao nước dềnh bằng 0.2% đến
14% độ cao sóng ngoài khơi. Giá trị này nhỏ
tại cửa sông rộng và sâu, ngược lại tại các
cửa sông hẹp và nông thì ảnh hưởng của
nước dềnh là rất đáng kể.
Đã phát triển thành công mô hình giải tích
đơn giản tính toán biến thiên nước dềnh tại
khu vực cửa sông. Kết quả so sánh với số liệu
thực nghiệm thể hiện mô hình có tính dự báo
và độ chính xác tương đối cao.
5. TÀI LIỆU THAM KHẢO
[1] Bowen, A.J., Inman, D.L. and Simmons,
V.P., 1968: Wave ‘set-down’ and set-up,
Journal of Geophysical Research, Vol.73,
No.8, pp.2569-2577.
[2] Komar, P.D.,Gaughan,M.K., 1972: Airy
wave theory and break height prediction.
Proceedings of 13th International
Conference on Coastal Engineering, Vol.1,
pp. 405–418.
[3] Longuet-Higgins, M.S., Stewart, R.W.,
1963: A note on wave set-up. Journal of
Marine Research,Vol.21, pp. 4–10.
[4] Sunamura, T. 1983: A predictive model for
shoreline changes on natural beaches caused
by storm and post-storm waves,
Transactions, Japanese Geomorphological
Union, Vol.4, pp.1-10.
[5] Tinh N. X., Tanaka H., Umeda M., Sasaki
M. and Nagabayashi H. 2009: Wave setup
due to the extreme events at different river
mouth morphologies in Japan, Journal of
Hydroscience and Hydraulic Engineering
JSCE, Vol.53, pp.199-204.