MÔ HÌNH PORTFOLIO

MÔ HÌNH PORTFOLIO

CHƯƠNG 8

Financial Modeling 15

8.1 TỔNG QUAN

Khung tình huống • Hàm mục tiêu: TSSL danh mục -> Max Hoặc RR danh mục -> Min • Biến số ra quyết định: Tỷ trọng đầu tư vào các chứng khoán (xi) • Ràng buộc: - Ràng buộc về vốn đầu tư. - Ràng buộc về đầu tư hết. - Giới hạn về trần rủi ro hoặc sàn TSSL. - Ràng buộc về bán khống và đa dạng hóa.

1

Financial Modeling 16

8.2 CÁC KÝ HIỆU

• E(ri) là tỷ suất sinh lợi mong đợi của tài sản i • Var(ri) phương sai của tỷ suất sinh lợi tài sản

i

• Cov(ri;rj) là hiệp phương sai của giữa tài sản i

và tài sản j. Cov(ri;rj) là σij

• Var(ri) là σii

Financial Modeling 17

8.3 MÔ HÌNH 2 CHỨNG KHOÁN

• Từ số liệu giá đóng cửa vào cuối mỗi tháng (tuần,

ngày) của mỗi cổ phiếu, chúng ta tính toán tỷ suất sinh lợi hàng tháng (tuần, ngày) của mỗi cổ phiếu.

=

ln

r At

P At P

tA

- 1,

   

   

• Đây là công thức tính theo kỳ ghép lãi liên tục, trong

trường hợp có cổ tức, chúng ta có thể tính: +

Div

t

=

ln

r At

P At P

- 1,

tA

   

   

2

Financial Modeling 18

8.3 MÔ HÌNH 2 CHỨNG KHOÁN • Giả định rằng các dữ liệu tỷ suất sinh lợi trong 12 tháng qua thể hiện phân phối tỷ suất sinh lợi của cổ phiếu này trong những tháng (tuần, ngày) sắp tới. • Tính TSSL mong đợi như sau:

n

=

r

jr

∑

1 N

= 1j

• Tính phương sai của TSSL:

N

=

Var

(

r

r

2)

j

∑

1 N

= 1

j

• Tính hiệp phương sai giữa 2 chứng khoán

A,B

-

,

)

[

[*)]

)]

rCov ( A

r B

r At

rE ( A

r Bt

rE ( B

1 = ∑ N

t

- -

Financial Modeling 19

8.3 MÔ HÌNH 2 CHỨNG KHOÁN

• Sử dụng các hàm Average( ), Varp( ), và Stdevp( ) và COVAR() trong Excel để tính TSSL mong đợi, Phương sai, độ lệch chuẩn và hiệp phương sai.

• Tính toán hệ số tương quan giữa chứng

khoán:

)r,r(Cov BA

=

AB

BA

• Hoặc dùng hàm Correl () trong Excel Hệ số tương quan luôn luôn nằm giữa +1và –1 hay –1≤ ρAB≤+1 • • Nếu hệ số tương quan là +1, khi đó tỷ suất sinh lợi giữa 2 chứng khoán có

tương quan xác định hoàn toàn.

• Nếu hệ số tương quan là –1, khi đó tỷ suất sinh lợi giữa 2 chứng khoán sẽ

có tương quan phủ định hoàn toàn.

r s s

3

Financial Modeling 20

8.3 MÔ HÌNH 2 CHỨNG KHOÁN

• Giá trị trung bình tỷ suất sinh lợi của danh mục là bình quân

gia quyềnvới trọng số là tỷ lệ vốn ñầu tư vào mỗi cổ phiếu

thành phần.

• Gọi xA là tỷ trọng vốn ñầu tư vào cổ phiếu A, ta có:

• E(rp) = xAE(rA) + (1–xA)E(rB)

• Phương sai danh mục không phải là bình quân gia quyền

của các phương sai (vì có mối tương quan trong biến ñộng

TSSL của các cổ phiếu)

• Var(rp) = xA

2 Var(rA) + (1– xA)2 Var(rB) + 2 xA(1–xA)Cov(rA,rB)

• σp

2 = xA

2 σA

2 + (1– xA)2 σB

2 + 2 xA(1–xA)ρABσAB

Financial Modeling 21

8.3 MÔ HÌNH 2 CHỨNG KHOÁN

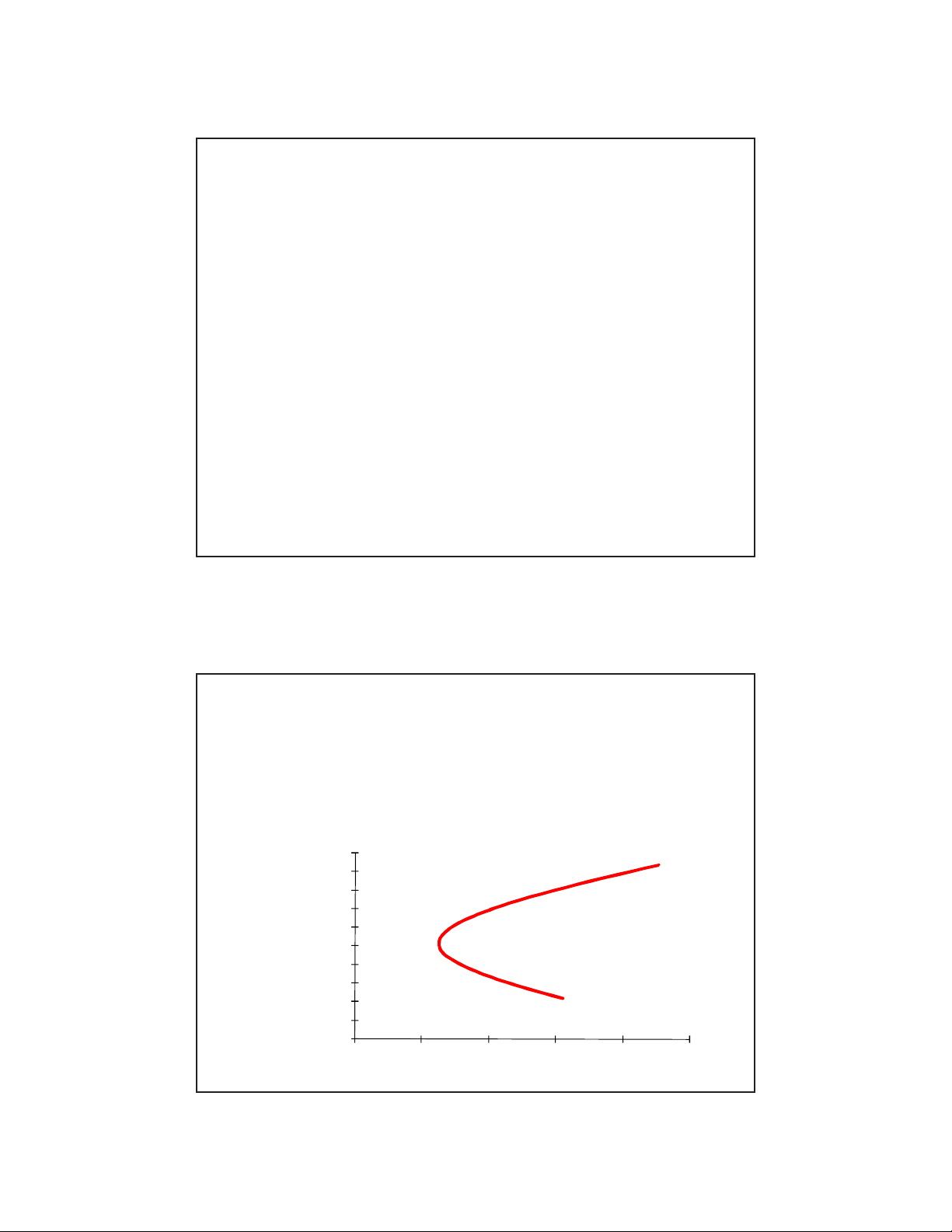
• Đường hiệu quả danh mục:

ðường hiệu quả của danh mục

3.50%

3.45%

3.40%

3.35%

c ụ m h n a d

3.30%

a ủ c

3.25%

3.20%

n â u q h n

ì

3.15%

3.10%

b L S S T

3.05%

3.00%

3.50%

4.50%

5.50%

6.50%

7.50%

8.50%

Financial Modeling 22

ðộ lệch chuẩn của danh mục

4

8.4 MÔ HÌNH NHIỀU CHỨNG KHOÁN

• Trong trường hợp tổng quát với N chứng khoán (hay N tài sản), giả định rằng tỷ lệ vốn đầu tư vào chứng khoán i trong danh mục là xi, như vậy ta có ma trận cột X các tỷ trọng vốn đầu tư vào danh mục như sau:

x

1

x

2

=

x

X

    3  ....   x 

       

n

• Chúng ta có thể viết XT như là ma trận đảo của ma trận cột X: • XT = [x1, x2, x3, ….xn]

Financial Modeling 23

8.4 MÔ HÌNH NHIỀU CHỨNG KHOÁN

• Bây giờ ta viết E(r) như là ma trận cột của tỷ suất sinh lợi

các chứng khoán

=

)r(E

)r(E 1 )r(E 2 )r(E 3

     ....   

       

)r(E N • E(r)T như là ma trận hàng của tỷ suất sinh lợi các chứng

khoán:

• E(r)T = [E(r1), E(r2), E(r3), ….E(rn)]

5

Financial Modeling 24

8.4 MÔ HÌNH NHIỀU CHỨNG KHOÁN

• Tỷ suất sinh lợi mong đợi của danh mục dưới

dạng công thức ma trận như sau:

N

T

T

=

=

X)r(E)r(EX)r(Ex

)r(E p

i

i

=∑

1i

• Hoặc có thể dùng hàm SUMPRODUCT () của 2

vector hàng hoặc 2 vector cột.

-

Financial Modeling 25

8.4 MÔ HÌNH NHIỀU CHỨNG KHOÁN

• Phương sai danh mục: • Gọi ma trận có σij trong hàng thứ i và cột thứ j là ma

trận phương sai – hiệp phương sai:

...

11

12

13

N1

s s s s

...

21

22

23

N2

s s s s

=

...

S

N3

32 .....

33 .....

.....

s s s s

...

NN

3N

1N

    31  .....   

       

2N • Phương sai của danh mục là Var(rp) = XTSX

s s s s

6

Financial Modeling 26

8.5 TÍNH TOÁN MA TRẬN HIỆP PHƯƠNG SAI

• Cách 1: • Dựa trên công thức thống kê và các hàm của Excel, chúng ta có thể tính ma trận phương sai – hiệp phương sai:

• A là ma trận chênh lệch tỷ suất sinh lợi các

....

chứng khoán

1

- -

....

r N r N

2

r N r N

=

A

r 1 r 1 ....

.....

- -

....

 r 11  r  12  ....  

     

r 1

M

r 1

r NM

r N

- - Financial Modeling 27

8.5 TÍNH TOÁN MA TRẬN HIỆP PHƯƠNG SAI

• Ma trận chuyển vị của ma trận A:

....

....

r 1

r 12

r 1

r M1

r 1

- - -

....

....

r N

r 2N

r N

r NM

r N

 r 11  .....   r  1N

    

tính như sau:

• Ma trận phương sai – hiệp phương sai được ] [ s= =

S

ij

T A.A M

- - -

7

Financial Modeling 28

8.5 TÍNH TOÁN MA TRẬN HIỆP PHƯƠNG SAI

• Sử dụng hàm COVAR kết hợp với hàm Offset

• Hàm Covar(array1;array2…): dùng để tính hiệp phương sai của 2 mảng dữ liệu (2 chuỗi TSSL quan sát)

• Hàm Offset(initial cells, rows, columns) sẽ tham chiếu khối các ô tương đồng về hình dáng với các ô gốc ban đầu nhưng thay đổi vị trí sang các hàng và cột khác.

b+

Financial Modeling 29

8.5 TÍNH TOÁN MA TRẬN HIỆP PHƯƠNG SAI ~ a= R

~ R

x

i

i

~ e+ i

• Mô hình chỉ số đơn i • Giả định của mô hình là tỷ suất sinh lợi của mỗi một tài sản có thể được hồi quy tuyến tính từ các chỉ số của thị trường:

a=

b+

(E

(E

~ )R i

i

~ )R x

i

• Từ đó, chúng ta có 2 lập luận: lập luận thứ nhất giống mô hình CAPM và lập luận thứ 2 dùng để tính ma trận phương sai – hiệp phương sai: b=

ij

i

j

2 x

s b s

8

Financial Modeling 30