TR NG Đ I H C S PH M K THU T TP.HCMƯỜ Ạ Ọ Ư Ạ Ỹ Ậ
KHOA: ĐI N TỆ Ử
B MÔN: C C K THU T ĐI N TỘ Ơ Ở Ỹ Ậ Ệ Ử
Tên h c ph n: TR NG ĐI N Tọ ầ ƯỜ Ệ Ừ Mã h c ph n:0141040ọ ầ
S ĐVHT:3ố
Trình đ đào t o:Đ i h cộ ạ ạ ọ
A - NGÂN HÀNG CÂU H I KI M TRA ĐÁNH GIÁ KI U T LU N.Ỏ Ể Ể Ự Ậ
Ch ng 1: M Đ Uươ Ở Ầ
Các n i dung ki n th c t i thi u mà sinh viên ph i n m v ng sau khi h c xong ch ng 1 ộ ế ứ ố ể ả ắ ữ ọ ươ
Các đ i l ng vect đ c tr ng cho tr ng đi n t :ạ ượ ơ ặ ư ườ ệ ừ
E: vect c ng đ đi n tr ng ơ ườ ộ ệ ườ
H: vect c ng đ t tr ng ơ ườ ộ ừ ườ
D:vect điơ ện cảm
B: vect tơ ừ cảm
J: vect m t đ dòng điơ ậ ộ ện dẫn
H ph ng trình Maxwell :ệ ươ
RotH = J +
t
D
∂
∂
rotE = -
t
B
∂
∂
divB = 0
divD = ρ
D=εE; B=μH; J=γE
Bài toán 1:cho đi n tr ng E ,tìm t tr ng H = ?ệ ườ ừ ườ
Bài toán 2: cho t tr ng H,tìm đi n tr ng E = ? ừ ườ ệ ườ
Bài toán 3: cho đi n tr ng E ,tìm ệ ườ
?=
ρ
Các m c tiêu ki m tra đánh giá và d ng câu h i ki m tra đánh giá g i ý ch ng 1ụ ể ạ ỏ ể ợ ươ
M c tiêu ki m tra đánh giáụ ể N i dungộ
M c đ Nh ứ ộ ớ các ki n th c c n nh :ế ứ ầ ớ
RotH = J +
t
D
∂
∂
rotE = -
t
B
∂
∂
divB = 0
1
Bi u m u 3aể ẫ
divD = ρ
D=εE; B=μH; J=γE
M c đ Hi u đ c cácứ ộ ể ượ
ki n th c đã h c ế ứ ọ Hi u các ý nghĩa c a hể ủ ệ ph ng trình Maxwell:ươ
a) 2 ph ng trình (1) và (2) nêu lên m i quan h khăng khít gi aươ ố ệ ữ
tr ng đi n bi n thiên và tr ng tườ ệ ế ườ bi n thiênừ ế
b) 2 ph ng trình (3) và (4) nêu lên d ng hình h c c a tr ngươ ạ ọ ủ ườ
đi n vệ à tr ng tườ ừ
c) C 4 ảph ng trình nêu lên m i quan h khăng khít gi a tr ngươ ố ệ ữ ườ
đi n tệ và môi tr ng ch từ ườ ấ
Kh năng v n d ng cácả ậ ụ
ki n th c đã h c ế ứ ọ các ki n th c mà sinh viên ph i bi t v n d ng :ế ứ ả ế ậ ụ
sinh viên ph i bi t cách tính các toán t vect nh grad,div,ả ế ử ơ ư
rot,divgrad trong các h tr c t a đ khác nhau b ng cách s d ngệ ụ ọ ộ ằ ử ụ
b ng các toán t vect đã đ c cho tr c.ả ử ơ ượ ướ
Kh năng t ng h p: ả ổ ợ Bài toán 1:cho đi n tr ng E ,tìm t tr ng H = ?ệ ườ ừ ườ
Bài toán 2: cho t tr ng H,tìm đi n tr ng E = ? ừ ườ ệ ườ
Bài toán 3: cho đi n tr ng E ,tìm ệ ườ
?=
ρ
Ngân hàng câu h i và đáp án chi ti t ch ng 1ỏ ế ươ
tt Lo iạN i dungộĐi mể
1 Câu h iỏCho tr ng đi n ườ ệ
( )
αα α
sin.cos.
1
2ee
r
Er+=
.Hãy tính ρ=? 1
Đáp án Theo ph ng trinh Maxwell,ta có ươ ρ= divD =div(εE)= εdivE
Trong h tr c t a đ tr ta có:ệ ụ ọ ộ ụ
divE =
=
0
coscos
33 =+
−
rr
αα
v y ậ
0=
ρ
1
2 Câu h iỏTrong môi tr ng ườ ε=const, µ=const, γ=0, có tr ng đi nườ ệ
z
etbyaxE .cos.sin.sin
ω
=
1.Tìm H =?
2.CMR :
µεω
..
222 =+ ba
2,5
Đáp án Ta có :
1
2
Z
E
r
E
rr
rE zr
∂
∂
+
∂
∂
+
∂
∂
α
α
)(
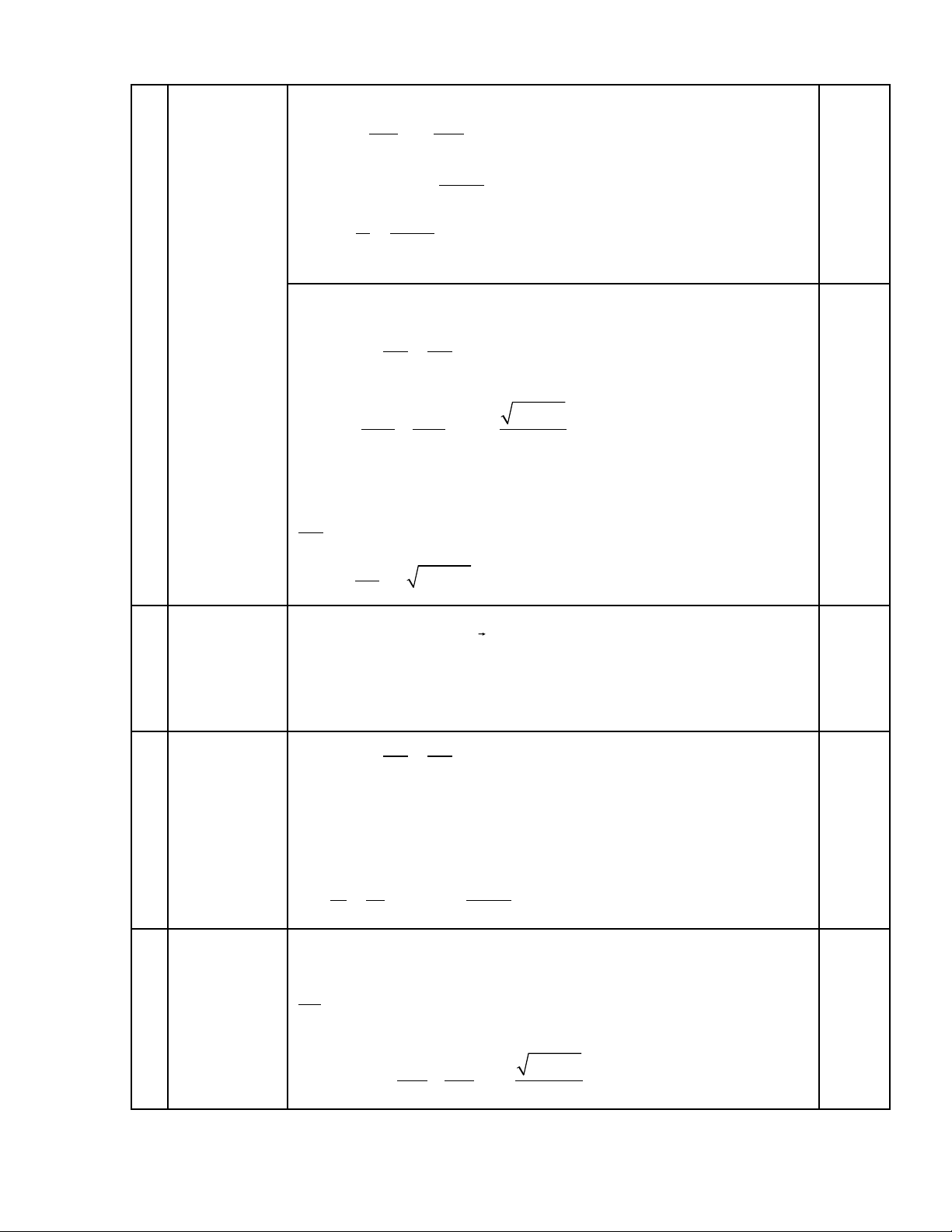
mà
cos ( cos sin cos sin )
y
z
x y x y
E
E
rotE e e t b by axe a ax bye
y x
ω
∂
∂
= − = −
∂ ∂
sin ( cos sin . sin cos . )
y x
t
B rotEdt a ax by e b ax by e
ω
ω
→ = − = −
∫
0
sin ( cos sin . sin cos . )
y x
B t
H a ax by e b ax by e
ω
µ µ ω
→ = = −
Ta có :
( 0)
D D
rotH J J E
t t
γ
∂ ∂
= + = = =
∂ ∂
2 2
0
( ) sin sin sin .
yx
z z
HHa b
rotH e ax by t e
x y
ω
ωµ
∂∂+
= − = −
∂ ∂
Mà :
0
0
sin sin cos .
sin sin sin .
z
z
D E ax by t e
Dax by t e
t
ε ε ω
ε ω ω
= =
∂= −
∂
2 2 2
0 0
D
rotH a b
t
ω ε µ
∂
= → + =
∂
1.5
3 Câu h iỏTrong môi tr ng ườ ε=const, µ=const, γ=0, có tr ng tườ ừ
z
etbyaxH .cos.sin.sin
ω
=
1.Tìm E =?
2.CMR :
µεω
..
222 =+ ba
2,5
Đáp án
( 0)
D D
rotH J J E
t t
γ
∂ ∂
= + = = =
∂ ∂
mà
sin cos cos . cos sin cos .
x y
rotH b ax by t e a ax by t e
ω ω
= −
suy ra:
0 0
1 sin ( cos sin . sin cos . )
y x
D t
E rotHdt a ax by e b ax by e
ω
ε ε ωε
= = = −
∫
1
Ta có :
0
0
sin sin cos .
sin sin sin .
z
z
B H ax by t e
Bax by t e
t
µ µ ω
µ ω ω
= =
∂= −
∂
Mà :
2 2
0
( ) sin sin sin .
yx
z z
EEa b
rotE e ax by t e
x y
ω
ωε
∂∂+
= − =
∂ ∂
1,5
3
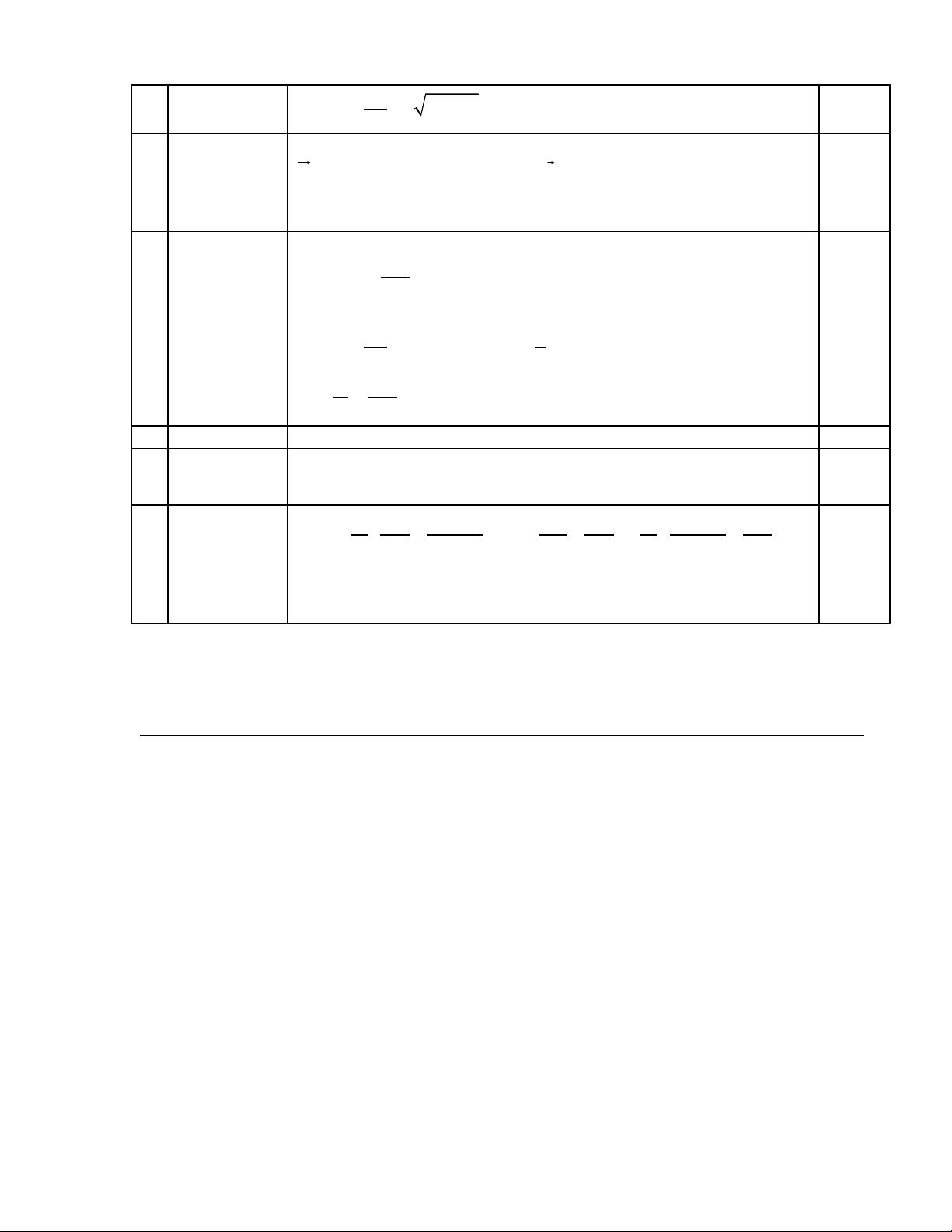
2 2 2
0 0
B
rotE a b
t
ω ε µ
∂
= − → + =
∂
4 Câu h iỏTrong môi tr ng ườ ε=ε , µ=µ , γ=0, có tr ng đi nườ ệ
( )
x
ezttzE
ππ
4.010.6cos.100),( 7−=
1.Tìm H =?
2.Tr ng đi n trên có tính ch t th hay không?ườ ệ ấ ế
2
Đáp án Ta có:
( )
7
4 cos 6 10 0.4
x
y y
E
rotE e e t z
z
π π π
−
∂
= − = − −
∂
mà :
( )
( )
7
7
0
2sin 6 10 0.4
3
2sin 6 10 0.4
3
y
y
B
rotE B rotEdt t z e
t
B
H t z e
π π
π π
µ µ
−
−
∂
= − → = − = −
∂
= = −
∫
1,5
Vì
0rotE ≠
nên tr ng đi n đã cho không có tính ch t thườ ệ ấ ế 0,5
5 Câu h iỏCho tr ng đi n ườ ệ
2 3
r z
E e .5r e .r.cos e .r
φ
= + φ+
ur ur uur uur
. Tr ng đi n trênườ ệ
có tính ch t th hay không?ấ ế
1
Đáp án
( ) ( )
2
3 2cos 0
r z r z z r
z
rE rE
e E E E e E
rotE e
r z z r r r
r e e
α α
α
α
α α
α
∂ ∂
∂ ∂ ∂ ∂
= − + − + − =
÷ ÷
÷
∂ ∂ ∂ ∂ ∂ ∂
= − + ≠
v y tr ng đi n không có tính ch t thậ ườ ệ ấ ế
1
Ch ng 2: TR NG ĐI N T TĨNHươ ƯỜ Ệ Ừ
Các n i dung ki n th c t i thi u mà sinh viên ph i n m v ng sau khi h c xong ch ng 2ộ ế ứ ố ể ả ắ ữ ọ ươ
Các đ i l ng vect đ c tr ng cho tr ng đi n tĩnh:ạ ượ ơ ặ ư ườ ệ
D: vect điơ ện cảm
,E: vect c ng đ đi n tr ngơ ườ ộ ệ ườ
Các đ i l ng vect đ c tr ng cho tr ng t tĩnh:ạ ượ ơ ặ ư ườ ừ
B: vect tơ ừ cảm
H: vect c ng đ t tr ngơ ườ ộ ừ ườ
H ph ng trình Maxwell c a tr ng đi n t tĩnhệ ươ ủ ườ ệ ừ
tr ng đi n tĩnhườ ệ
rotE = 0; divD = ρ;
E: vect c ng đ đi n tr ngơ ườ ộ ệ ườ
D:vect điơ ện cảm; D=εE
tr ng t tĩnhườ ừ
RotH = 0; divB = 0;
4
H: vect c ng đ t tr ng ơ ườ ộ ừ ườ
B: vect tơ ừ cảm; B=μH
Bài toán 1: Tìm đi n tr ng ệ ườ
E
ur
,
D
ur
, ϕ = ? b ng ph ng pháp gi i ph ng trình Laplace-Poissonằ ươ ả ươ
Bài toán 2: Tìm đi n tr ng ệ ườ
E
ur
,
D
ur
, ϕ= ? b ng ph ng pháp s d ng đ nh lu t Gauss . ằ ươ ử ụ ị ậ
Các m c tiêu ki m tra đánh giá và d ng câu h i g i ý ch ng 2ụ ể ạ ỏ ợ ươ
M c tiêu ki m tra đánh giáụ ể N i dungộ
M c đ Nh ứ ộ ớ các ki n th c c n nh :ế ứ ầ ớ
a) ph ng trình Laplace-Poisson: ươ ∆φ = -ρ/ε
b) đ nh lu t Gauss: ị ậ
.
s
D ds q=∑
∫Ñ
M c đ Hi u ứ ộ ể -sinh viên c n ph i hi u : tr ng đ ên tĩnh và tr ng t tĩnh là haiầ ả ể ườ ị ườ ừ
m t c a tr ng đ ên t tĩnh, chúng hoàn toàn đ c l p v i nhau.ặ ủ ườ ị ừ ộ ậ ớ
-sinh viên ph i hi u các tính ch t c a tr ng đi n tĩnh,khái ni mả ể ấ ủ ườ ệ ệ
v năng l ng tr ng đi n , đi n dung:ề ượ ườ ệ ệ
-năng l ng tr ng đi n :ượ ườ ệ
2
1 1 1
. . .
2 2 2
E
V
W D EdV QU C U= = =
∫
-đi n dung : ệ
Q
CU
=
Kh năng v n d ng cácả ậ ụ
ki n th c đã h c ế ứ ọ sinh viên ph i bi t v n d ng ph ng trình Laplace – Poisson vàả ế ậ ụ ươ
đ nh lu t Gauss đ tìm tr ng đi n tĩnh..ị ậ ể ườ ệ
Kh năng t ng h p: ả ổ ợ Bài toán 1: Tìm đi n tr ng ệ ườ
E
ur
,
D
ur
, ϕ = ? b ng ph ng pháp gi iằ ươ ả
ph ng trình Laplace-Poisson?ươ
Bài toán 2: Tìm đi n tr ng ệ ườ
E
ur
,
D
ur
, ϕ= ? b ng ph ng pháp sằ ươ ử
d ng đ nh lu t Gauss ? ụ ị ậ
Ngân hàng câu h i thi và đáp án chi ti t ch ng 2ỏ ế ươ
tt Lo iạN i dungộĐiể
m
1 Câu
h iỏCho qu c u bán kính aả ầ , mang đi n tích v i m t đ đi n tích kh i ệ ớ ậ ộ ệ ố ρ=kR,đ tặ
môi tr ng không khí.ườ Hãy xác đ nh ị
E
ur
,
D
ur
, ϕ do qu c u này gây ra b ngả ầ ằ
ph ng pháp s d ng đ nh lu t Gaussươ ử ụ ị ậ ? (bi t r ng th t i tâm c a qu c uế ằ ế ạ ủ ả ầ
b ng 0 vàằ môi tr ngườ trong qu c u cóả ầ ε=const).
2,5
Đáp
án Söû duïng h tr c t a đ c u (ệ ụ ọ ộ ầ HTTÑC), ta coù:
0;0;0 =
∂
∂
=
∂
∂
≠
∂
∂
θφ
R
0.5
Tröôøng hôïp 1: R < a 1
5