KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 88 (3/2024)
50
BÀI BÁO KHOA HỌC
NGHIÊN CỨU ỨNG DỤNG THUẬT TOÁN ĐIỀU KHIỂN TRƯỢT
CHO ĐIỀU KHIỂN QUỸ ĐẠO CHUYỂN ĐỘNG CỦA ROBOT SCARA
Đoàn Yên Thế
1
, Nguyễn Xuân Biên
1
Tóm tắt: Một trong những yêu cầu bắt buộc khi thiết kế, chế tạo và điều khiển Robot là phải xây dựng
quỹ đạo chuyển động dành cho Robot. Để đảm bảo việc điều khiển quỹ đạo chuyển động của Robot bám
sát với quỹ đạo đặt cho trước cần lựa chọn bộ điều khiển phù hợp nhất và từ đó tính toán các tham số
của bộ điều khiển. Bài báo này nghiên cứu ứng dụng thuật toán điều khiển trượt (SMC) áp dụng xây
dựng quỹ đạo chuyển động cho robot SCARA ba bậc tự do (3-Dof). Thuật toán này giải quyết được vấn
đề kháng nhiễu cao giúp hệ thống hoạt động ổn định nên được sử dụng để điều khiển cho cả hệ thống
tuyến tính và phi tuyến. Để làm rõ khả năng kháng nhiễu khi ứng dụng thuật toán này, bài báo này so
sánh các đáp ứng quỹ đạo chuyển động của robot khi sử dụng bộ điều khiển trượt và bộ điều khiển PID.
Kết quả mô phỏng được trình bày bằng phần mềm Matlab-Simulink cho thấy bộ điều khiển trượt hoạt
động tốt trong cả hai trường hợp có nhiễu và không có nhiễu, giúp cho quỹ đạo thực của robot bám với
quỹ đạo đặt cho trước.
Từ khóa: Robot SCARA, 3-Dof, điều khiển trượt (SMC), quỹ đạo chuyển động.
1. ĐẶT VẤN ĐỀ
*
Robot công nghiệp là những thiết bị tự động
linh hoạt, thực hiện các chức năng lao động công
nghiệp của con người dưới một hệ thống điều
khiển theo những chương trình đã được lập trình
sẵn. Việc nghiên cứu phát triển robot công nghiệp
bao gồm hai vấn đề chính cần thực hiện đó là tính
toán, thiết kế, chế tạo cơ khí cho robot và lựa
chọn, tính toán bộ điều khiển phù hợp. Về mặt
thiết kế chế tạo cơ khí cho robot ngày càng hoàn
thiện với các công cụ trong tính toán thiết kế mô
phỏng. Trong bài báo này tác giả muốn tập trung
nghiên cứu về mặt điều khiển cho robot. Cụ thể
hóa là nhóm tác giả lựa chọn mô hình robot
SCARA 3-DoF làm mục tiêu nghiên cứu về việc
điều khiển quỹ đạo chuyển động.
Loại robot SCARA là một trong những loại
robot phổ biến trong công nghiệp, được giới thiệu
và sản xuất tại Nhật Bản vào năm 1979 (Shimon
Y. Nof, 1999), kể từ đó đã được nhiều nhà sản
xuất áp dụng và phát triển. Do khả năng thích ứng
cũng như chức năng của robot SCARA giúp giảm
chi phí sản xuất của các sản phẩm, đặc biệt là các
1
Khoa Cơ khí, Trường Đại học Thủy lợi
hàng điện tử, điều này giúp mang lại nhiều ưu thế
so với các đối thủ cạnh tranh. Bất chấp sự phát
triển liên tục của các loại robot, SCARA vẫn được
sử dụng rất rộng rãi với các ứng dụng đa năng của
nó. Điển hình như robot SG400 của hãng
YASKAWA (Hình 1) là một trong những loại
robot SCARA thông dụng ngày nay. Robot
SCARA có ưu điểm là độ chính xác và tốc độ cao
do cấu trúc nhẹ, kích thước nhỏ gọn, chuyển động
linh hoạt ổn định… SCARA được sử dụng ở các
kích cỡ khác nhau trong tất cả các ngành công
nghiệp như điện tử, ô tô, và y học….
Về mặt điều khiển, thuật toán PID đã được sử
dụng hầu hết cho các ngành điều khiển robot. Cụ
thể với robot SCARA, thuật toán này cũng đã
được trình bày trong một số tài liệu như điều
khiển mô hình robot SCARA 2-Dof (M. Kemal
Ciliz, et al 2005), thiết kế xây dựng và điều khiển
mô hình SCARA 3-Dof (M. S. Dutra, et al 2007),
thiết kế phát triển robot SCARA 4-Dof (K. S.
Mohamed Sahari, et al 2012), hay mô hình hóa và
điều khiển PID cho robot SCARA 3-Dof (M. A.
Sen, et al 2017) đã biểu diễn mô hình robot trên
SolidWorks và chuyển đổi sang Matlab/Simulink.
Tuy nhiên thuật toán PID không cung cấp độ
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 88 (3/2024)
51
chính xác cao cho các yêu cầu làm việc tốc độ cao
của robot khi mà có những sự thay đổi đột ngột
của tham số hoặc các trường hợp có tác động của
nhiễu ngoại. Hơn nữa, các mô hình chính xác của
hệ thống robot đều là mô hình phi tuyến với các
hiệu ứng ma sát và thay đổi của tải do đó việc sử
dụng bộ điều khiển PID sẽ mang đến hiệu suất
thấp. Để khắc phục điều này, một thuật toán điều
khiển tốt hơn đã được áp dụng đó là điều khiển
trượt (SMC). Thuật toán này được sử dụng cho cả
điều khiển hệ thống tuyến tính và phi tuyến.
Hình 1. Robot SG400
Đã có một số kết quả nghiên cứu ứng dụng
thuật toán điều khiển trượt cho robot SCARA về
việc tiết kiệm năng lượng cho robot SCARA 2-
Dof bằng cách sử dụng điều khiển trượt (L. A.
Soriano, et al 2021), tuy nhiên trong nghiên cứu
chưa đề cập đến trường hợp có nhiễu tác động. Có
một số bài báo đã nghiên cứu điều khiển trượt khi
robot hoạt động ở tốc độ cao (M.C. Lee, et al
1995) và bộ điều khiển trượt thích nghi cho robot
SCARA 3-Dof (F. Adelhedi, et al 2015), tuy nhiên
kết quả của nghiên cứu chưa thể hiện rõ kết quả áp
dụng thuật toán điều khiển trượt so với bộ điều
khiển PID khi có nhiễu tác động.
Bài báo này tập trung nghiên cứu ứng dụng
thuật toán điều khiển trượt SMC để điều khiển
quỹ đạo chuyển động cho robot SCARA 3-Dof
trong các trường hợp có và không có tác động của
nhiễu. Hơn nữa kết quả mô phỏng thể hiện sự
khác biệt giữa điều khiển trượt SMC và thuật toán
điều khiển PID. Các kết quả mô phỏng được xây
dựng trên phần mềm Matlab-simulink có thể áp
dụng cho việc chế tạo thử nghiệm robot với áp
dụng của bộ điều khiển mới.
2. PHƯƠNG PHÁP NGHIÊN CỨU
2.1. Mô hình toán học robot Scara
Theo các tài liệu nghiên cứu bộ điều khiển trượt
thích nghi (F. Adelhedi, et al 2015) và bộ quan sát
nhiễu cho robot SCARA (A. Dehak, et al 2019),
mô hình động học của robot SCARA 3-Dof có liên
kết cứng được trình bày như công thức (1):
()+(,)+()=−′ (1)
Trong đó với n=3:
∈
: là vecto vị trí đo của khớp nối.
∈
: là vecto tốc độ đo của khớp nối.
∈
: là vecto gia tốc đo của khớp nối.
()∈

là ma trận quán tính, bị chặn và
xác định dương.
(,)∈
: Là ma trận ly tâm Coriolis.
()∈
: là vecto lực hấp dẫn.
=∈
: là vecto momen điều khiển bên
ngoài, hay chính là vecto lực tác động tại mỗi khớp.
′∈
: là vecto momen nhiễu phi tuyến tác
động đến các khớp như ma sát, giảm chấn…
Từ mô hình toán học sẽ đi đến thiết kế bộ điều
khiển cho robot. Với bộ điều khiển PID cơ bản,
tham số bộ điều khiển được tính toán dựa trên bộ
PID toolbox, tác giả sẽ không trình bày cấu trúc
điều khiển, bài báo này sẽ tập trung vào trình bày
cấu trúc của bộ điều khiển trượt.
2.2. Thuật toán điều khiển trượt
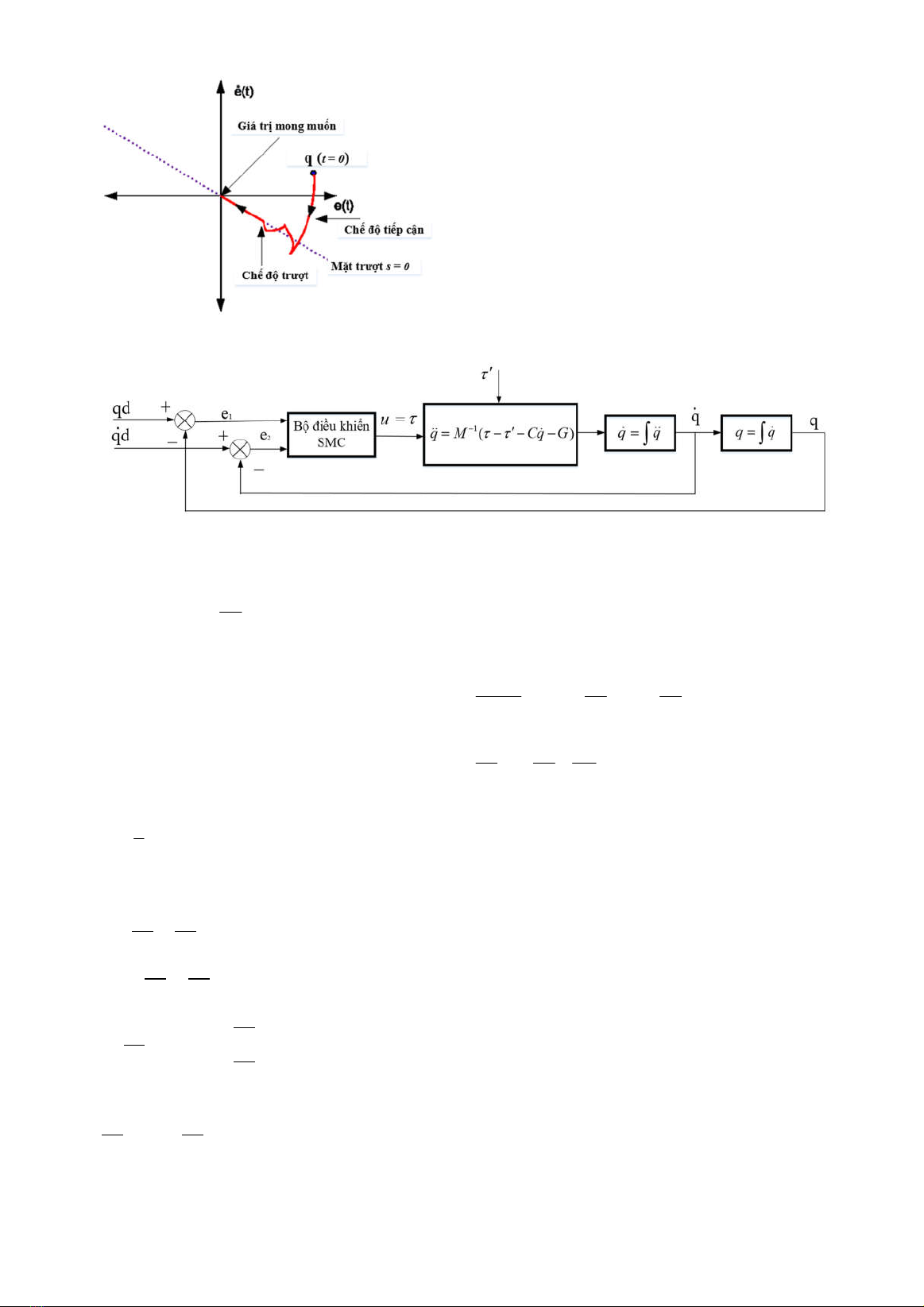
Điều khiển trượt là phương pháp điều khiển
dựa trên thiết kế của luật điều khiển chuyển mạch
tốc độ cao nhằm điều khiển quỹ đạo của hệ thống
trên bề mặt trượt (Hình 2). Điều khiển trượt đã
được nghiên cứu rộng rãi trong nhiều năm (V.
Utkin, 1992) và được sử dụng rộng rãi trong các
ứng dụng thực tế điển hình như các hệ thống cơ
điện (V. Utkin, et al 1999). Các ưu điểm chính của
điều khiển trượt cần phải kể đến bao gồm cấu trúc
đơn giản, thời gian hội tụ hữu hạn, đáp ứng động
học tốt và bất biến trước các thay đổi và nhiễu của
tham số. Hiệu suất của hệ thống được đảm bảo bởi
tính bền vững của điều khiển trượt ngay cả khi các
tham số hoặc mô hình không chắc chắn chính xác.
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 88 (3/2024)
52
Hình 2. Điều khiển trượt SMC
Áp dụng phương pháp điều khiển trượt trên cơ
sở cấu trúc động lực học robot. Từ mô hình động
học của robot (1) chuyển vế ta thu được:
1
( )q M Cq G
q q
q q
(2)
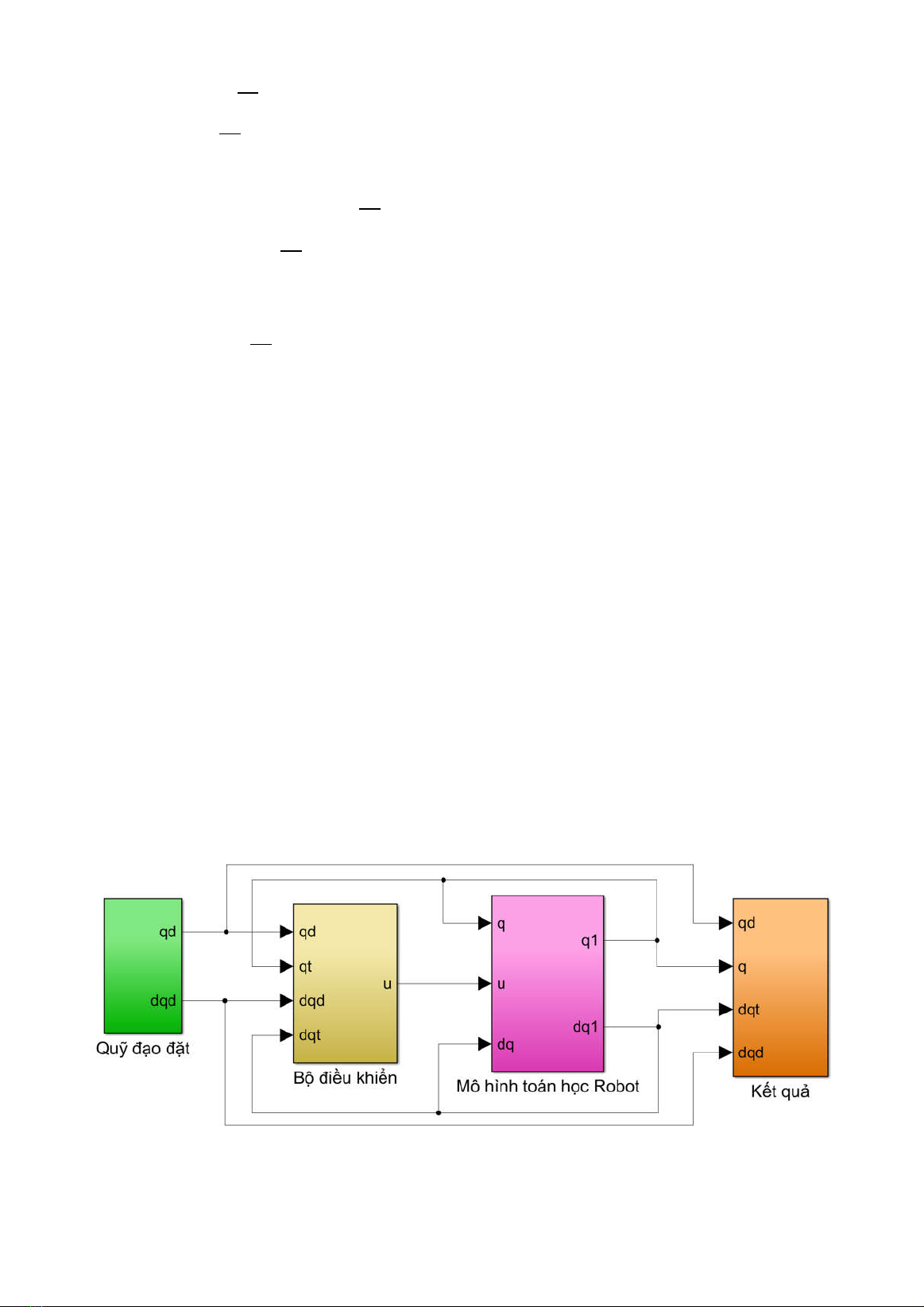
Áp dụng công thức (2), sơ đồ hệ thống điều
khiển trượt cho Robot có dạng:
Hình 3. Sơ đồ hệ thống điều khiển trượt SMC
Chọn mặt trượt tuyến tính có dạng:
1 0 1 2
( )s e a e e= +
và
1
2
de e
dt =
(3)
Ở đây
1d
e q q= -
là sai lệch vị trí,
2d
e q q
là sai lệch tốc độ,
0
a
là tham số mặt trượt. Chọn
0
0a
để phương trình
0
( )P s a s
thỏa mãn đa
thức Hurwitz.
Để đảm bảo tính ổn định của hệ thống, sử dụng
lý thuyết ổn định Lyapunov, hàm Lyapunov có
dạng như sau:
2
1 1
1
( )
2
V s s
=
(4)
Tiếp theo, nhiệm vụ thiết kế điều khiển sao cho
1
( ) 0V s
·<
tại vùng lân cận của điểm cân bằng. Do
đó, ta có:
1 1
1
( ) 0 0
dV s ds
s
dt dt
< Û < 11
sgn( (e)) 0
ds s
dt
Û <
(5)
Mặt khác:
1 1 2
0
ds de de
a
dt dt dt
= +
(6)
Thay công thức (6) vào công thức (5) thu được:
Thay công thức (6) vào công thức (5) thu được:



+



()<0 (7)
↔


+


=<0ℎ
()>0
>0ℎ
()<0 (8)
↔


=<−


ℎ
()>0
>−


ℎ
()<0 (9)
Suy ra:

=−


−

()∀
>0 (10)
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 88 (3/2024)
53
↔
−=−


−

()∀
>0 (11)
↔=
+


+

() (12)
Thay
q
từ công thức (2) vào (12) thu được:

(−
−−)=
+

+
(
()) (13)
↔==
+


+
(
())+++
(14)
Từ công thức (14), coi giá trị của nhiễu là không biết trước và tín hiệu điều khiển không phụ thuộc
vào ảnh hưởng của nhiễu ta thu được:

=
+


++

=
(
()) (15)
Trong đó: +
eq
u
là thành phần kéo sai lệch vị trí
tiến đến mặt trượt.
+
sw
u
là thành phần giữ sai lệch vị trí trượt trên
mặt trượt và tiến về giá trị 0.
Công thức (15) là các đại lượng đặc trưng của bộ
điều khiển trượt, được sử dụng để xây dựng bộ điều
khiển quỹ đạo chuyển động cho mô hình robot
SCARA 3-Dof. Đối với luật điều khiển trượt cơ bản,
các tham số a
0
và k
0
cần phải thỏa mãn điều kiện
dương. Khi a
0
và k
0
càng lớn, thời gian hội tụ càng
nhanh, tuy nhiên việc lựa chọn giá trị a
0
và k
0
sẽ ảnh
hưởng đến năng lượng hệ thống. Giá trị a
0
và k
0
càng lớn sẽ cần nguồn cấp năng lượng càng cao.
3. KẾT QUẢ VÀ THẢO LUẬN
3.1. Mô hình xây dựng trên phần mềm
Matlab-Simulink
Bài toán đặt ra: Thiết kế quỹ đạo chuyển động
của robot di chuyển theo một quỹ đạo cho trước
trong khoảng thời gian 5s, kiểm tra đáp ứng
chuyển động của các biến khớp khi có và không
có nhiễu tác động. Quỹ đạo đặt của các biến khớp
có dạng:
1
2
3
0.5sin(1.4 )
0.6sin(2 )
280 10 (2.5 )
d
d
d
q t
q t
q sign t
(16)
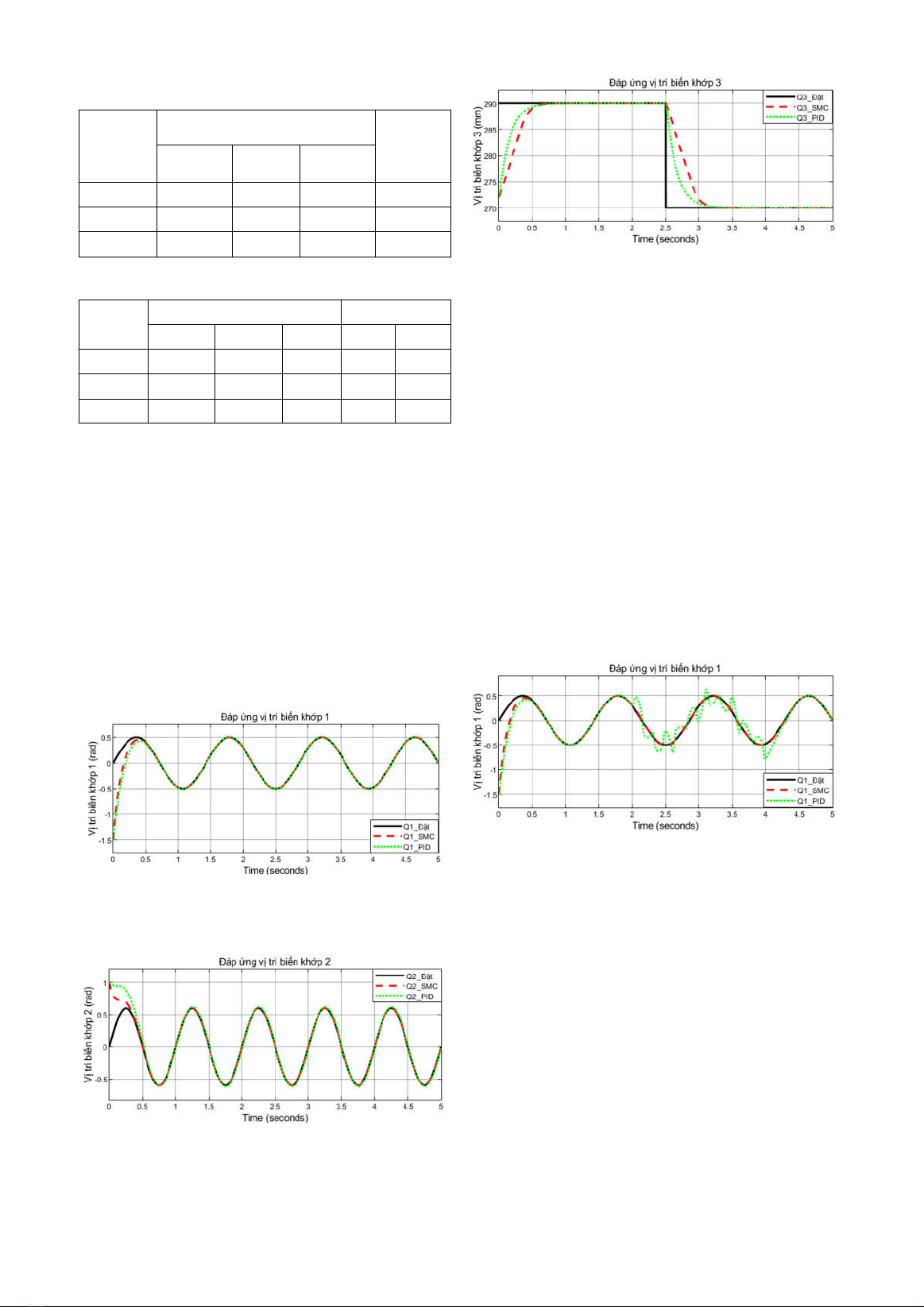
Sử dụng phần mềm Matlab-Simulink để xây
dựng tính toán mô phỏng quỹ đạo chuyển động
cho robot Scara. Mô hình hệ thống được biểu diễn
như Hình 4 bao gồm các khối: quỹ đạo đặt, bộ
điều khiển (SMC hoặc PID), mô hình toán học
Robot và kết quả mô phỏng. Tham số mô hình và
tham số bộ điều khiển được sử dụng có giá trị như
trong Bảng 1 và Bảng 2.
Hình 4. Mô hình hệ thống mô phỏng điều khiển cho Robot SCARA
KHOA HỌC KỸ THUẬT THỦY LỢI VÀ MÔI TRƯỜNG - SỐ 88 (3/2024)
54
Bảng 1. Tham số mô hình
Khâu Vị trí trọng tâm (mm) Khối
lượng
(kg)
x
c
y
c
z
c
1 -250 0 0 5
2 -225
0 0 5
3 0 0 -150
5
Bảng 2. Tham số bộ điều khiển
Khâu PID Trượt
P I D a
0
k
0
1 3658 235.5 132 200 150
2 1890 124.5 89.4 200 150
3 2037 108.6 115 150 120
3.2. Kết quả mô phỏng
Trường hợp 1: Khi không có nhiễu tác động:
0
Với kết quả mô phỏng, đáp ứng vị trí của từng
biến khớp được thể hiện như (Hình 5,6,7). Kết quả
cho thấy với cả hai bộ điều khiển PID và điều
khiển trượt SMC, giá trị thực của vị trí biến khớp
bám sát giá trị đặt. Thời gian đáp ứng của biến
khớp 1, 2 là khoảng 0,5s và thời gian đáp ứng của
biến khớp 3 là khoảng 0,7s.
Hình 5. Đáp ứng vị trí biến khớp 1
khi không có nhiễu tác động
Hình 6. Đáp ứng vị trí biến khớp 2
khi không có nhiễu tác động
Hình 7. Đáp ứng vị trí biến khớp 3
khi không có nhiễu tác động
Trường hợp 2: Khi có nhiễu tác động: 0
Để kiểm tra sự hiệu quả của bộ điều khiển
trượt trong việc kháng nhiễu, tại thời điểm 2s =>
4s ta bổ sung một nhiễu phi tuyến có dạng hình
sine
0.8*sin(10 *t)
1.2*sin(10 * )
0
t
tác động vào khớp 1
và khớp 2 của robot. Nhiễu tác động
được
đưa vào mô hình bằng cách cộng trực tiếp với
tín hiệu điều khiển u theo công thức (14). Giá trị
của Kết quả mô phỏng được thể hiện trong
Hình 8 và Hình 9.
Hình 8. Đáp ứng vị trí biến khớp 1
khi có nhiễu tác động
Kết quả cho thấy khi có nhiễu tác động, với bộ
điều khiển PID, quỹ đạo chuyển động của các biến
khớp bị dao động mạnh, như trong Hình 8 ta thấy
rằng độ quá điều chỉnh lớn nhất sấp sỉ 50%, với
Hình 9 độ quá điều chỉnh lớn nhất lên đến 150%.
Đối với bộ điều khiển trượt SMC, khi có nhiễu tác
động, quỹ đạo chuyển động của các biến khớp vẫn
bám sát theo giá trị đặt, sai lệch quỹ đạo là không
đáng kể, điều đó chứng tỏ bộ điều khiển trượt
SMC giúp cho robot luôn hoạt động chính xác
theo quỹ đạo cho trước.