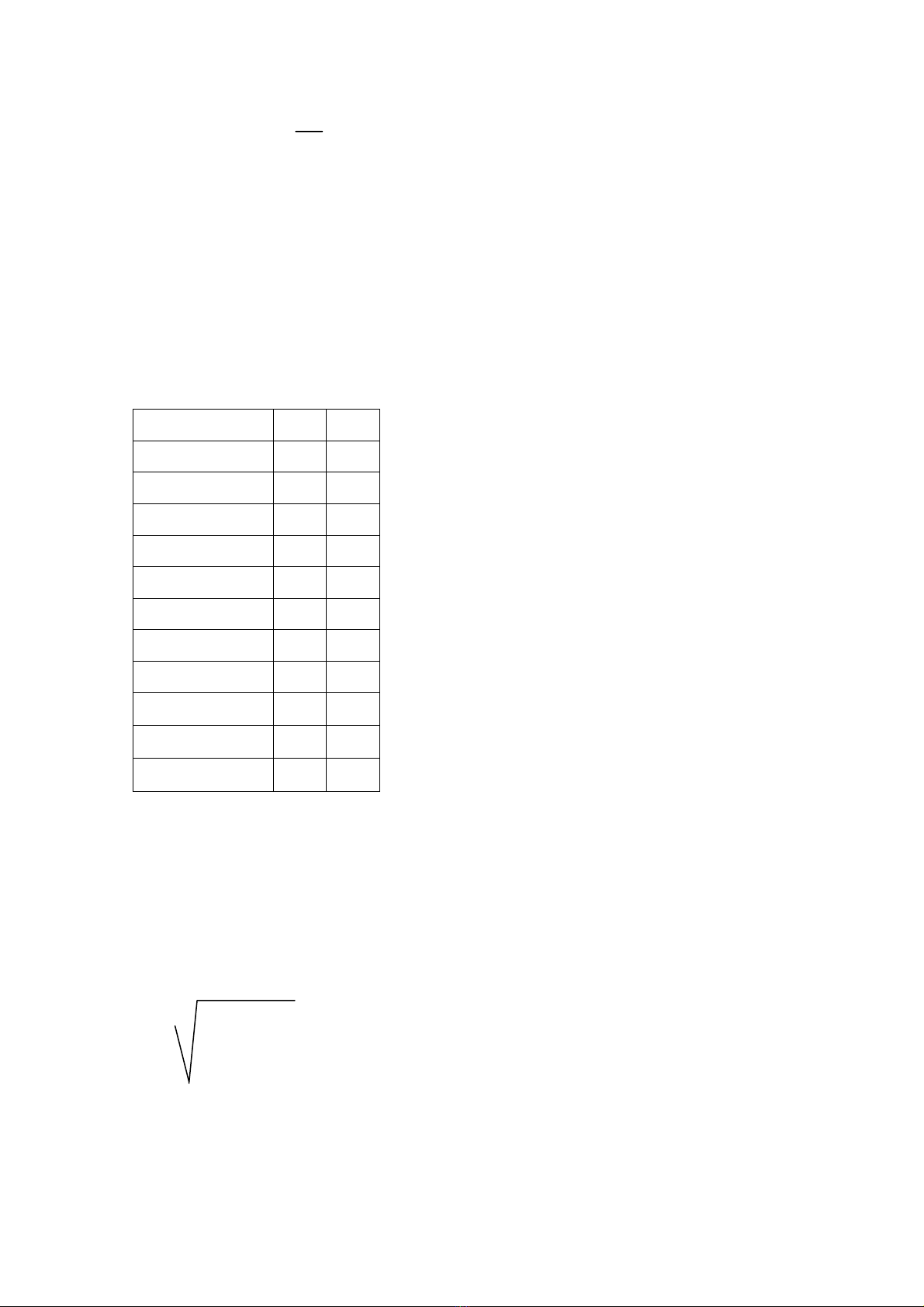
- Tìm T lý thuyết với bậc tự do là 9; α = 0,025: Ta tìm hàm TINV(9, 0,05)= 2,262;
Như vậy, ⎜T ⎜ kiểm định = 3,456 >T lý thuyết = 2,262 ta bác bỏ Ho, nghĩa là năng
suất lao động của công nhân sau khi áp dụng công nghệ mới khác với công nghệ cũ.
Vì Ď = 4,9 > Do nên µx - µy > 0, nghĩa là ở mức ý nghĩa 5% áp dụng công nghệ
mới đã làm tăng năng suất so với công nghệ cũ.
b) Trường hợp lấy mẫu độc lập:
+ Bài toán:
Giả sử ta có nx và ny là số đơn vị mẫu được chọn ngẫu nhiên, độc lập từ hai tổng thể
X và Y có phân phối chuẩn, thể hiện ở bảng sau:
Quan sát X Y
1 X1 Y1
2 X2 Y2
3 X3 Y3
. . .
. . .
N Xn Yn
Số quan sát nx n
y
Trung bình mẫu x ŷ
Trung bình µx µy
Phương sai δ2x δ2y
Độ lệch chuẩn δ x δy
+ Nguyên tắc kiểm định: Có 2 trường hợp xảy ra
1) Nếu nx ,ny ≥ 30, với X, Y tuân theo phân phối chuẩn và δ2 x ≠ δ2y
Tính tiêu chuẩn kiểm định Z (Z thực nghiệm):
µx Trung bình của tổng thể X
µy Trung bình của tổng thể Y
x
ˆ, ŷ là trung bình của 2 mẫu chọn ngẫu nhiên từ
2 tổng thể X ; Y
δ2 x và δ2y là phương sai của tổng thể X và Y
Với mức ý nghĩa α, cần kiểm định giả thuyết sau:
Ho: µx - µy = Do (Do là giá trị cho trước Do=0)
H1: µx - µy ≠ Do
Hay:
Ho: µx - µy = 0 ; H1: µx - µy ≠ 0
Trong đó:
– ŷ‐Dx
ˆo Do : Giá trị cụ thể cho trước (Do =0)
Z = --------------- , ŷ : Trung bình của 2 mẫu x
ˆ
δ2x δ2y δ2 x và δ2y : Phương sai của tổng thể X và Y
----- + ------ nx ,ny : Số đơn vị mẫu quan sát của tổng thể X và Y
nx ny Z: Tiêu chuẩn kiểm định (Z thực nghiệm)
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 100
- Tìm Z lý thuyết:
Tìm Zα/2 bằng cách tra bảng hoặc dùng hàm NORMSINV với α/2 trong EXCEL.
Quy tắc kiểm định được tóm tắt như sau:
Giả thuyết Bác bỏ Ho khi
Ho : µx - µy = Do
H1 : µx - µy ≠ Do
Z > Zα/2 hoặc Z <- Zα/2
hay ⎜Z⎜> Zα/2
Ho : µx - µy = Do hoặc µx - µy ≥ Do ;
H1 : µx - µy < Do
Z <- Zα
Ho : µx - µy = Do hoặc µx - µy ≤ Do ;
H1 : µx - µy > Do
Z > Zα
Chú ý:
+ Nếu ⎜Z⎜ ≤ Zα/2 ta chấp nhận giả thuyết Ho, coi µx - µy = Do
+ Nếu ⎜Z⎜ > Zα/2 ta bác bỏ giả thuyết Ho, coi µx - µy ≠ Do và khi đó :
Nếu > ŷ ta xem µx > µy
x
ˆ
Nếu < ŷ ta xem µx < µy
x
ˆ
+ Nếu chưa biết phương sai của tổng thể, mà số đơn vị mẫu lớn (nx ,ny ≥ 30 ) ta vẫn
dùng công thức trên để tính Z kiểm định, thay phương sai tổng thể bằng phương sai mẫu
(δ2 x = s2x và δ2y= s2y ).
Thí dụ: Một trại chăn nuôi gà tiến hành thí nghiệm sử dụng 2 loại thức ăn A và B
trên cùng một giống. Sau một thời gian thử nghiệm cho ăn, người ta điều tra 50 con
nuôi bằng thức ăn A và 40 con nuôi bằng thức ăn B thu được các số liệu sau:
Bảng 5.6. Một số chỉ tiêu của 2 mẫu thí nghiệm cho ăn 2 loại thức ăn A và B
Diễn giải ĐVT Thức ăn A Thức ăn B
1. Số đơn vị mẫu quan sát con 50 40
2. Khối lượng trung bình 1 con Kg/con 2,2 1,2
3. Độ lệch chuẩn Kg/con 1,25 1,02
Yêu cầu: Anh, chị hãy cho biết khối lượng trung bình 1 con sử dụng ở 2 loại thức
ăn sau thời gian nuôi có khác nhau không với mức ý nghĩa là 5%?
Giải:
- Gọi µx và µy là khối lượng trung bình 1 con sau khi nuôi sử dụng thức ăn A và
B;
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 101
- Đặt giả thuyết: Ho : µx - µy = 0
H1 : µx - µy ≠ 0
- Tính tiêu chuẩn kiểm định Z:
– ŷ‐D
x
ˆo 2,2 - 1,2 - 0 1
Z = -------------------- = ---------------------------- = --------- = 4,179
δ2x δ2y 1,252 1,022 0,2392
------ + ------ ------- + --------
nx ny 50 40
- Tìm Z lý thuyết qua hàm NORMSINV với α = 0,025 trong EXCEL ta được Z lý
thuyết = 1,96.
- ⎜Z⎜= 4,179 > Zα/2 = 1,96 ta bác bỏ giả thuyết Ho, coi µx - µy ≠ 0.
Vì =2,2 kg/con > ŷ = 1,2 kg/con nên ta xem µx > µy, chứng tỏ khối lượng
trung bình 1 con nuôi bằng thức ăn A lớn hơn nuôi bằng thức ăn B.
x
ˆ
2) Nếu nx, ny < 30 với X; Y đều tuân theo phân phối chuẩn và δ2 x = δ2y
Với mức ý nghĩa α, Ta cần kiểm định giả thuyết sau:
Ho: µx - µy = Do (Do là giá trị cho trước Do = 0)
H1: µx - µy ≠ Do
Hay:
Ho: µx - µy = 0 ; H1: µx - µy ≠ 0
- Tính tiêu chuẩn kiểm định T:
Trong đó:
– ŷ‐Dx
ˆo Do : Giá trị cụ thể cho trước (Do = 0)
T = -------------------- , ŷ : Trung bình của 2 mẫu x
ˆ
1 1 nx, ny: Số đơn vị mẫu quan sát của tổng thể
s2 ---- + ----- X và Y
nx ny T: Tiêu chuẩn kiểm định (T thực nghiệm)
s2 được tính theo công thức sau:
(nx-1) s2x + (ny- 1)s2y
s2 = -----------------------------
(nx + ny –2)
- T×m T lý thuyÕt:
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 102
Tõ α cho tr−íc, tra b¶ng ph©n phèi student víi bËc tù do lµ (nx + ny – 2) ®Ó t×m
T (nx + ny – 2; α/2) , hoÆc tra hµm TINV ((nx + ny – 2; α) trong EXCEL;
- Quy t¾c kiÓm ®Þnh ®−îc tãm t¾t nh− sau:
Gi¶ thuyÕt B¸c bá Ho khi
Ho : µx - µy = Do
H1 : µx - µy ≠ Do
T> Tnx + ny –2; α/2 hoÆc T <- T nx + ny –2; α/2
hay ⎜T⎜> T nx + ny –2; α/2
Ho : µx - µy = Do hoÆc µx - µy ≥ Do
H1 : µx - µy < Do
T < - T nx + ny –2; α
Ho : µx - µy = Do hoÆc µx - µy ≤ Do
H1 : µx - µy > Do
T > T nx + ny –2; α
- So s¸nh T thùc nghiÖm víi T lý thuyÕt:
NÕu ⎜T ⎜ ≤ T(nx + ny –2; α/2) ta chÊp nhËn gi¶ thuyÕt Ho.
NÕu ⎜T ⎜ > T(nx + ny –2; α/2) ta b¸c bá gi¶ thuyÕt Ho vµ khi ®ã:
NÕu > ŷ ta xem µx > µy
x
ˆ
Nếu < ŷ ta xem µx < µy
x
ˆ
Thí dụ: (Lấy lại ví dụ trên)
Một trại chăn nuôi gà tiến hành thí nghiệm sử dụng 2 loại thức ăn A và B trên cùng
một giống. Sau một thời gian thử nghiệm cho ăn, người ta điều tra 20 con nuôi bằng
thức ăn A và 15 con nuôi bằng thức ăn B thu được các số liệu sau:
Bảng 6.6. Một số chỉ tiêu của 2 mẫu thí nghiệm cho ăn 2 loại thức ăn A và B
Diễn giải ĐVT Thức ăn A Thức ăn B
1. Số đơn vị mẫu quan sát Con 20 15
2. Khối lượng trung bình 1 con Kg/con 2,2 1,2
3. Độ lệch chuẩn Kg/con 1,25 1,02
Yêu cầu: Anh chị hãy cho biết khối lượng trung bình 1 con sử dụng ở 2 loại thức ăn
sau thời gian nuôi có khác nhau không với mức ý nghĩa là 5%?
Giải:
- Gọi µx và µy là khối lượng trung bình 1 con sau khi nuôi sử dụng thức ăn A và
B;
- Đặt giả thuyết: Ho : µx - µy = 0
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 103
H1 : µx - µy ≠ 0
- Vì số mẫu quan sát nx, ny < 30, ta giả định phương sai của 2 tổng thể bằng nhau.
- Tính tiêu chuẩn kiểm định T:
- Tìm T lý thuyết:
Tra hàm TINV với bậc tự do là 33; α = 0,05 ta được T lý thuyết = 2,03.
Như vậy ⎜T ⎜ = 6,39 > T(nx + ny –2; α/2) = 2,03 ta bác bỏ giả thuyết Ho.
Vì x = 2,2 kg/con > ŷ = 1,2 kg/con nên ta xem µx > µy, chứng tỏ khối lượng
trung bình 1 con nuôi bằng thức ăn A lớn hơn nuôi bằng thức ăn B.
1.2.4. Kiểm định giả thuyết về sự bằng nhau giữa 2 phương sai của 2 tổng thể:
a) Bài toán
Giả sử ta có nx và ny là số đơn vị mẫu được chọn ngẫu nhiên, độc lập từ hai tổng thể
X và Y có phân phối chuẩn , thể hiện ở bảng sau:
Quan sát X Y
1 X1 Y1
2 X2 Y2
3 X3 Y3
. . .
. . .
n Xn Yn
Số quan sát nx n
y
Trung bình mẫu x ŷ
µx : Trung bình của tổng thể X
µy : Trung bình của tổng thể Y
x
ˆ , ŷ : Trung bình của 2 mẫu chọn ngẫu nhiên
từ 2 tổng thể X ; Y
δ2x và δ2y : Phương sai của tổng thể X và Y
s2x và s2y : Phương sai của 2 mẫu nx và ny
Với mức ý nghĩa α ta cần kiểm định
giả thuyết sau:
Ho : δ2x = δ2y
H1 : δ2x ≠ δ2y
– ŷ‐Dx
ˆo 2,2 - 1,2 - 0 1
T = -------------------- = ---------------------------- = --------- = 6,39
1 1 1 1 0,1564
s2 ---- + ---- 1,34 (------ + -----)
nx ny 20 15
s2 được tính theo công thức sau:
(nx-1) s2x + (ny- 1)s2y (20-1)1,252 + (15-1)1,022 44,2531
s2 = ------------------------ = ------------------------------- = --------------- = 1,34
( nx + ny –2) (20+15-2) 33
Trường Đại học Nông nghiệp Hà Nội – Giáo trình Nguyên Lỹ Thống kê…………………………… 104