π
/2
x
2
x
1
GV: Lê Văn Long – DĐ: 0915714848 – Tr ng THPT Lê L iườ ợ
Chúng ta bi t r ng t năm 2007 tr l i đây, B đã chuy n đ i hình th c thi môn v tế ằ ừ ở ạ ộ ể ổ ứ ậ
lý t t lu n sang tr c nghi m. V i cách thi nh v y đòi h i các em có r t nhi u k năng:ừ ự ậ ắ ệ ớ ư ậ ỏ ấ ề ỹ
k năng phân tích, d đoán, lo i tr ,… và đ c bi t là k năng gi i nhanh các bài toán.ỹ ự ạ ừ ặ ệ ỹ ả
Trong kỳ thi tuy n sinh 2012, Th y th y đa s các em đ u than th i gian quá ng n (so v iể ầ ấ ố ề ờ ắ ớ
đ ki n th c trong đ ) nên bài làm ch a th t t t l m. Trong ph m vi ki n th c c a mình,ề ế ứ ề ư ậ ố ắ ạ ế ứ ủ
Th y xin gi i thi u v i các em các cách gi i khác nhau c a m t s bài đi n hình trong đầ ớ ệ ớ ả ủ ộ ố ể ề
thi Đ i h c 2012. Sau đây là m t s ví d .ạ ọ ộ ố ụ
Có th có các cách gi i nh sau:ể ả ư
Cách 1: Gia s ư
cos Asinx A t v t
ω ω ω
= = −
.
* T i t: ạ
cosA t
ω
= 5.
* T i t + T/4: ạ
Asin Acos Acos 50
2
v t t v t
π
ω ω ω ω ω ω
� �
= − + = − = =
� �
� �
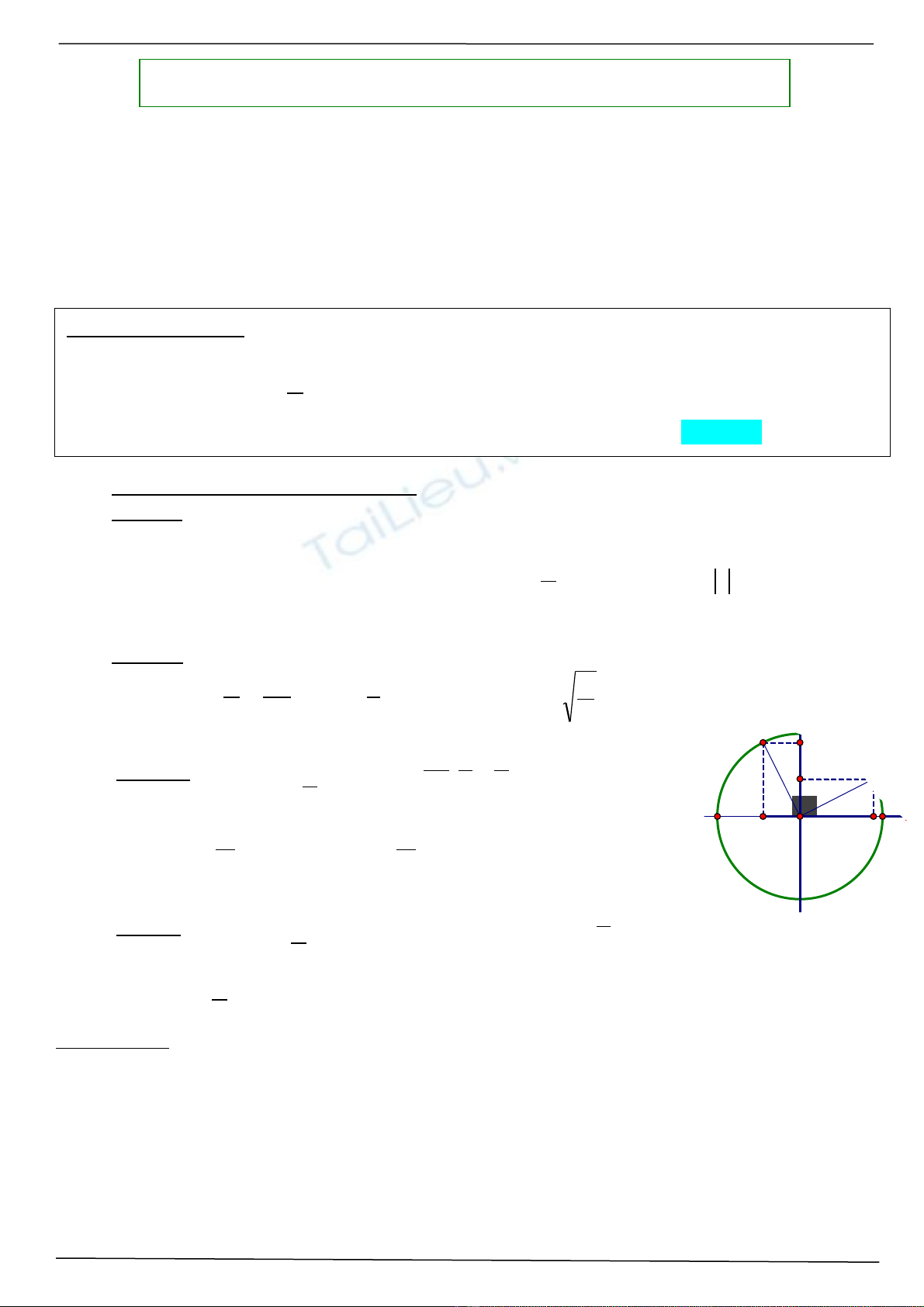
Cách 2: Hai v trí cách nhau T/4 => Hai v trí l ch pha nhau góc π/2. Theo đ ng trònị ị ệ ườ
l ng giác: ượ
A
v
A
x
ω
=
=> ω =
x
v
= 10rad/s. Mà
kgm
m
k0,1== >=
ω
(hình bên).
Cách 3: Ta có:
1
2 2 2
1 2
2
:2.4 2
:
4
t x Tx x A
TT
t x
π π
α
∆ = = + =� �
+
. M tặ
khác
2
2 2
2
2
v
x A
ω
� �
+ =
� �
� �
nên
2
22
1
0 1
v
x m kg
ω
� �
− = =�
� �
� �
(hình bên).
Cách 4 : Ta có
1 1
2 2
: ,
: ,
4
t x v
T
t x v
+
. Do kho ng th i gian là ả ờ
4
T
nên góc
quét
2
π
α
∆ =
. Áp d ng ụ
2 1
10 / 1 .v x rad s m kg
ω ω
= = =�� �
* Nh n xét:ậ Theo ý ki n c a cá nhân thì th y cách 3 gi i khá hay (vì ki n th c này theoế ủ ấ ả ế ứ
m ch t duy c a các em). Cách 1: có v dài h n và yêu c u các em n m ki n th c l ngạ ư ủ ẻ ơ ầ ắ ế ứ ượ
giác (chuy n t sin sang cos). Tuy nhiên, tùy s tr ng c a mình mà các em có th ch nể ừ ở ườ ủ ể ọ
cho mình cách gi i phù h p.ả ợ
NHỮNG CÁCH GI IẢ HAY TRONG ĐỀ VẬT LÝ
Câu 1 (mã đ ề 958 ): M t con l c lò xo g m lò xo nh có đ c ng 100N/m và v t nh kh iộ ắ ồ ẹ ộ ứ ậ ỏ ố
l ng m. Con l c dao đ ng theo ph ng ngang v i chu kì T. Bi t th i đi m t v t có lyượ ắ ộ ươ ớ ế ở ờ ể ậ
đ 5cm, th i đi m ộ ở ờ ể
4
T
t
+
v t có v n t c 50cm/s. Giá tr m b ngậ ậ ố ị ằ
A. 0,5kg. B. 1,2kg. C. 0,8kg. D. 1,0kg.
GV: Lê Văn Long – DĐ: 0915714848 – Tr ng THPT Lê L iườ ợ
Có th có cách gi i sau:ế ả
Cách 1: Do M, N là hai vân sáng và trên MN có 10 vân t i => có 10 kho ng vân => iố ả 1
= 2mm. M t khácặ:
3
10
5
3
2
2
1
2
1
== >==
i
i
i
λ
λ
mm => trên MN có
=
2
i
MN
6 kho ng vânả
=> có 7 vân sáng.
Cách 2:
* Khi
1
λ
: Do M, N là v trí c a 2 vân sáng và trên đo n MN = 20mm có 10 vân t i nênị ủ ạ ố
1
1
1
2( )
10 10. 20 .
D D mm
MN i mm
a a
λ
λ
= = = =
* Khi
2 1
2
1
5 2 10
: . . . .
3 3
s
D
x k k k mm
a
λ λ
λλ
= = =
. M là m t vân giao thoa, ta co thê chon ộ $ %
M O
, vi vây & % s vân sáng trên đo n OM b ng s vân sáng trên đo n MN. Do đó ố ạ ằ ố ạ sô vân sang cân$ $ &
tim la& &
10
0 . 20 0 6 7
3
k k N
 =����
(co thê chon $ %
10
10 . 10
3
k
−
).
Cách 3:
* Khi
1
λ
: Có 10 vân t i, mà M và N là hai vân sáng ố
có 11 vân sáng
có 10 kho ng vânả
i1 = 2mm.
* Khi
2
λ
: Do
2 1 2 1
5 5
3 3
i i
λ λ
= =�
(i t l v i ỷ ệ ớ
λ
)
có 6 kho ng vân ả
có 7 vân sáng.
Cách 4: Ta có
1
2i mm
=
(lý lu n nh trên). Do i t l ậ ư ỷ ệ
λ
nên
2
10
3
i mm
=
. T i M làạ
vân sáng nên s vân sáng trong kho ng MN là ố ả
2
20 1 7
s
Ni
= + =
.
Cách 5: Ta có
1
2i mm
=
(lý lu n nh trên) ậ ư
1
1
2( )
i a a mm
D D
λ
= =�
. Mà
1 2
2 2
5 10 10
( ) ( )
3 3 3
Da mm i mm
D a
λ λ
λ
= = = =� �
s vân sáng c n tìm: ố ầ
2
6
MN
ni
= =
s vân sáng 7.ố
* Nh n xét:ậ Nhìn chung các cách gi i đ u na ná nh nhau. Tùy s tr ng c a em mà ch nả ề ư ở ườ ủ ọ
cho mình cách gi i phù h p nh t.ả ợ ấ
Câu 4 (mã đ ề 958 ): Trong thí nghi m Y-âng v giao thoa ánh sáng, ngu n sáng phát ra ánhệ ề ồ
sáng đ n s c có b c sóng ơ ắ ướ
1
λ
. Trên màn quan sát, trên đo n th ng MN dài 20 mm (MNạ ẳ
vuông góc v i h vân giao thoa) có 10 vân t i, M và N là v trí c a hai vân sáng. Thay ánhớ ệ ố ị ủ
sáng trên b ng ánh sáng đ n s c có b c sóng ằ ơ ắ ướ
1
2
5
3
λ
λ
=
thì t i M là v trí c a m t vân giaoạ ị ủ ộ
thoa, s vân sáng trên đo n MN lúc này làố ạ
A.7. B. 5. C. 8. D. 6.
GV: Lê Văn Long – DĐ: 0915714848 – Tr ng THPT Lê L iườ ợ
Có th có các cách gi i sau:ể ả
Cách 1 (ph ng pháp lo i tr ):ươ ạ ừ Ta có R =
100 3
Ω
; ZC = 200Ω.
* N u ZếL > ZC. Đi u ki n t n t i: ề ệ ồ ạ
AM
ϕ
> π/3
ZL > 300 Ω
Đáp án A và B lo i.ạ
* ZL = Zc
Hi n t ng c ng h ng ệ ượ ộ ưở
0
tan 49
C
Z
R
ϕ ϕ
= =�
Lo i đáp án Dạ
Đáp án
đúng là A.
Cách 2 (dùng công th c):ứ Ta có:
3
AM
π
ϕ ϕ
− =
3
1 .
AM
AM
tg tg
tg tg
ϕ ϕ
ϕ ϕ
−=
+
3(1 . )
AM AM
tg tg tg tg
ϕ ϕ ϕ ϕ
− = +�
3 1 .
L C L C
L L
Z Z Z Z
Z Z
R R R R
− −
� � � �
− = +�� � � �
� � � �
( )
2
2 4
10 0 100 0
L L C L
Z Z Z Z− + = − =� �
1
100 .
L
Z L
π
= =� �
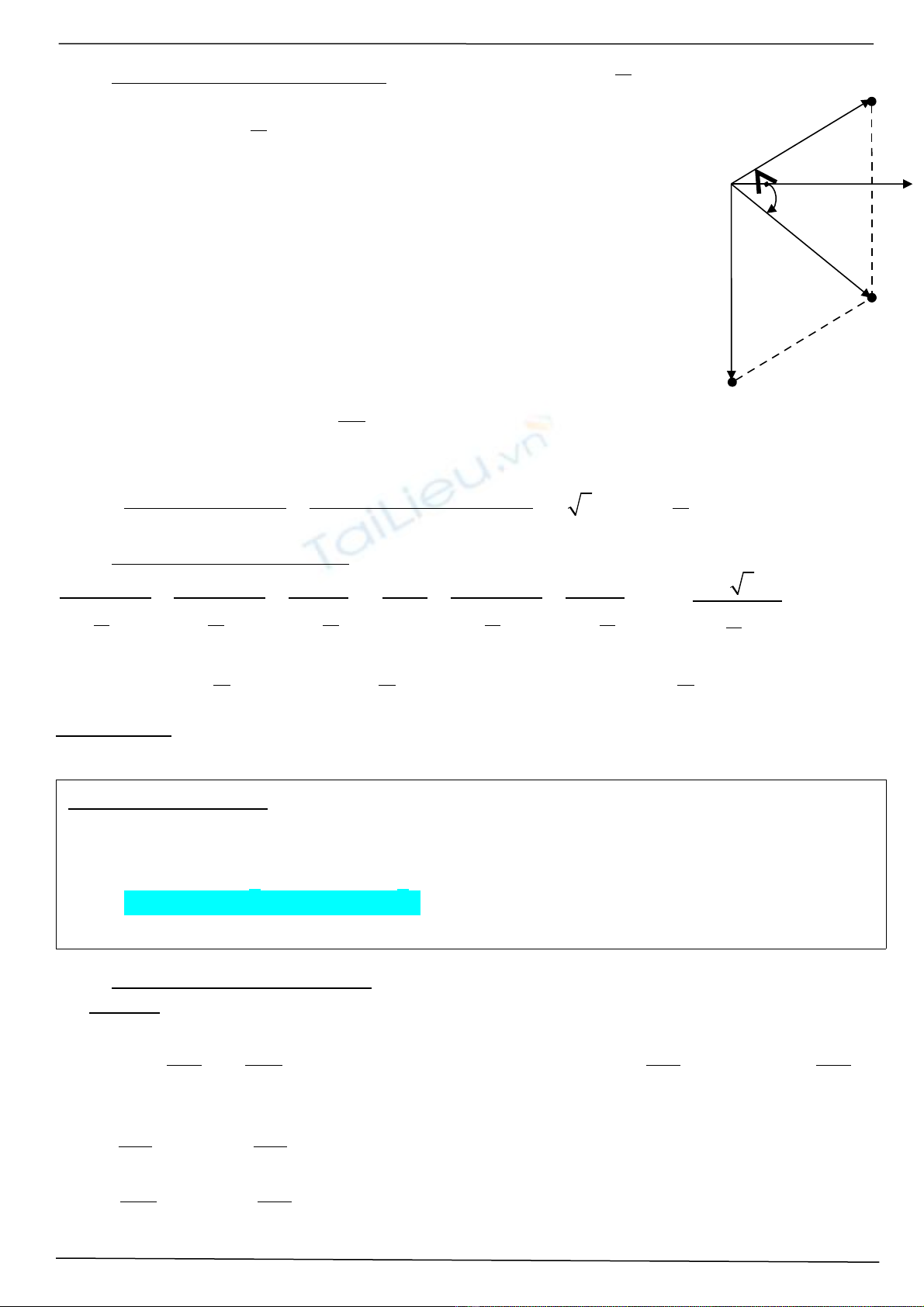
Cách 3 (dùng gi n đ véct ):ả ồ ơ Ta co $
3 3
2 2
C R C
R Z U U
= =� �
AM
OUU
∆
có đ ng cao ườ
3
2
R AM
OU U U
=
AM
OUU
∆
đ uề
tan 6
L R
U U
π
=
1.
3
L
R
Z L
π
= =� �
* Nh n xét:ậ Cách gi i 1 có v nhanh h n cách 2, tuy nhiên không ph iả ẻ ơ ả
bào nào c ng lo i tr đ c. Cách 2 là cách gi i c b n, dù h i dài.ủ ạ ừ ượ ả ơ ả ơ
Cách 3 yêu c u các em n m ch c gi n đ véct và ph i nhanh trongầ ắ ắ ả ồ ơ ả
vi c nh n xét ệ ậ
3
2
R C
U U
=
.
Có th có các cách gi i sau:ể ả
Câu 7 (mã đ ề 958 ): Đ t đi n áp u = Uặ ệ 0cos100πt (V) vào hai đ u đo n m ch AB g mầ ạ ạ ồ
hai đo n m ch AM và MB m c n i ti p. Đo n m ch AM g m đi n tr thu n ạ ạ ắ ố ế ạ ạ ồ ệ ở ầ
100 3
Ω
m c n i ti p v i cu n c m thu n có đ t c m L. Đo n m ch MB ch có t đi n có đi nắ ố ế ớ ộ ả ầ ộ ự ả ạ ạ ỉ ụ ệ ệ
dung
4
10
2F
π
−
. Bi t đi n áp gi a hai đ u đo n m ch AM l ch pha ế ệ ữ ầ ạ ạ ệ
3
π
so v i đi n áp gi aớ ệ ữ
hai đ u đo n m ch AB. Giá tr c a L b ngầ ạ ạ ị ủ ằ
A.
3H
π
.B.
2H
π
.C.
1H
π
.D.
2H
π
.
Câu 11 (mã đ ề 958 ): Hai dao đ ng cùng ph ng l n l t có ph ng trình xộ ươ ầ ượ ươ 1 =
1
cos( )
6
A t
π
π
+
(cm) và x2 =
6cos( )
2
t
π
π
−
(cm). Dao đ ng t ng h p c a hai dao đ ng này cóộ ổ ợ ủ ộ
ph ng trình ươ
cos( )x A t
π ϕ
= +
(cm). Thay đ i Aổ1 cho đ n khi biên đ A đ t giá tr c c ti uế ộ ạ ị ự ể
thì
A.
.
6rad
π
ϕ
= −
B.
.rad
ϕ π
=
C.
.
3rad
π
ϕ
= −
D.
0 .rad
ϕ
=
U
AM
O
U
R
U
C
U
L
π
/3
GV: Lê Văn Long – DĐ: 0915714848 – Tr ng THPT Lê L iườ ợ
Cách 1 (dùng công th c):ứ Ta có
1 1
cos( )
6
x A t cm
π
π
= +
;
2
6cos( )
2
x t cm
π
π
= −
. Biên đ dao đ ng t ng h pộ ộ ổ ợ
( )
2
2 2 2 2
1 2 1 2 1 1 1
2
2 os 6 36 3 27 27
3
A A A A A c A A A
π
� �
= + + = − + = − +
� �
� �
min 1
3A A A
= =�
. Khi đó
( ) ( )
( ) ( )
1 1 2 2
1 1 2 2
3sin / 6 6sin / 2
sin sin
tan 3 .
os os 3 os / 6 6 os / 2 3
A A
A c A c c c
π π
ϕ ϕ π
ϕ ϕ
ϕ ϕ π π
+ −
+
= = = − = −�
+ + −
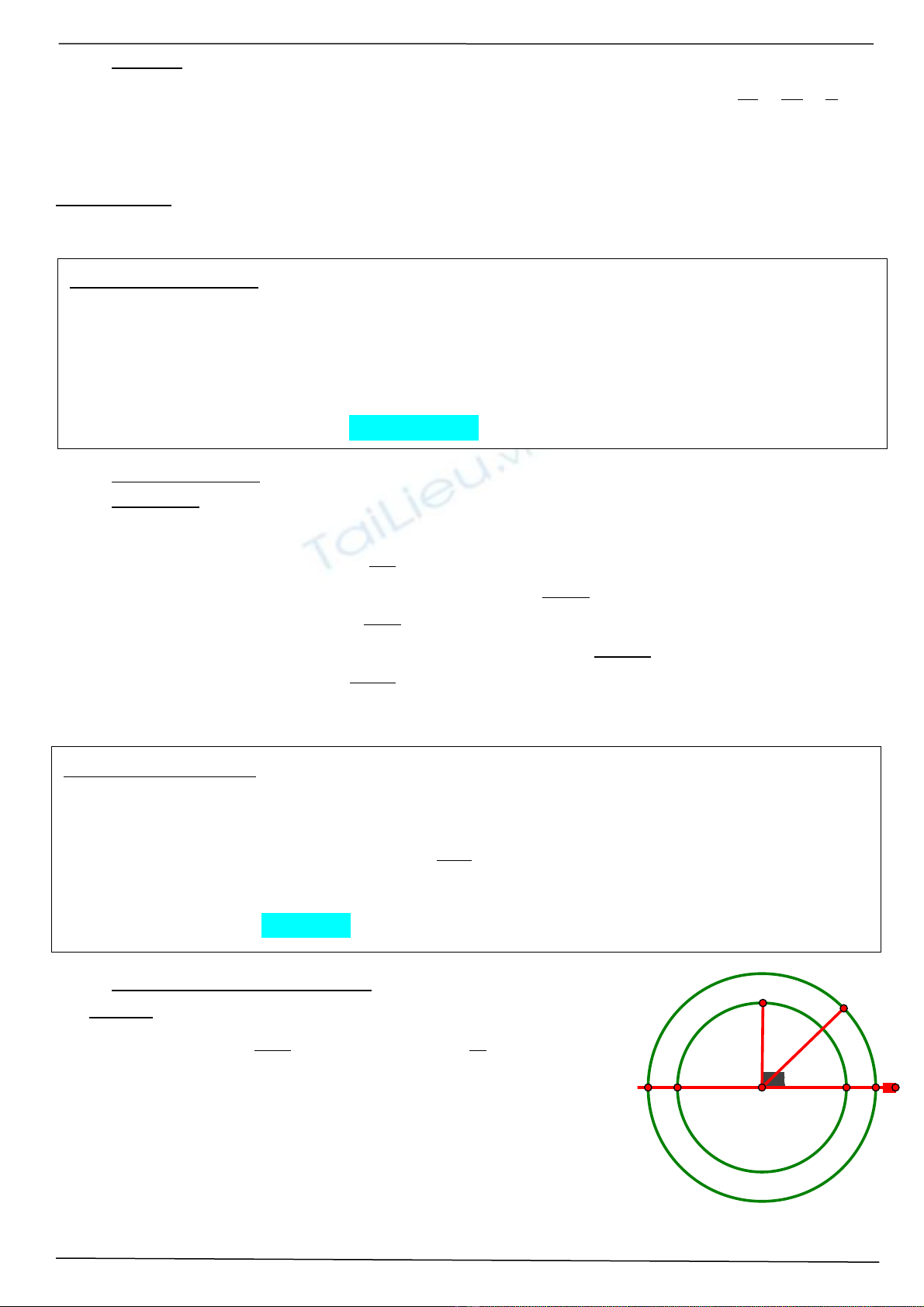
Cách 2 (dùng đ nh lý sin):ị Áp d ng đ nh lý sin cho ụ ị
∆
OA1A:
1 2 1
6
os
sin( ) sin( ) sin( ) sin( ) sin( )
2 6 3 6 3
A A A
A A
c
π π π π π
ϕ
ϕ ϕ ϕ
= = = =�
− + +
3 3
sin( )
6
A
πϕ
=�
+
min
:sin( ) 1
6 3
A A
π π
ϕ ϕ
= + = =� �
. Do
ϕ
d i tr c ướ ụ
∆
nên
3
π
ϕ
= −
.
* Nh n xét:ậ Cách 2 gi i nhanh h n nh ng yêu c u ả ơ ư ầ cac em $n m đ c đ nh lý sin và vắ ượ ị ẽ
đ c gi n đ véct .ượ ả ồ ơ
Có th có các cách gi i sau:ể ả
Cách 1: V trí vân có màu gi ng vân trung tâm t i đó có s trùngc a 2 vân sáng:ị ố ạ ự ủ
1 2 1 1
1 2 1 2 1 2 12 1 12 12 12 12
4 5 20 5 5 5
Min
D D D D
x x k k k k k k k x k x
a a a a
λ λ λ λ
= = = = = = =� � � � �
Trong kho ng 2 vân cùng màu vân trung tâm:ả
1 1
1 12min 1 1
2 1 2 2
2 12min
0 5. 0 5 1,2,3,4
0 4 1, 2,3
0 5.
D D
k x k k
a a
D D k k
k x
a a
λ λ
λ λ
< < =
< < =
� �
�
� � �
< < =
� �
< < =
Có 4 vân sáng
1
λ
; 3 vân sáng
2
λ
.
∆
1
A
r
2
A
r
A
r
/ 6
π
ϕ
O
Câu 18 (mã đ ề 958 ): Trong thí nghi m Y-âng v giao thoa ánh sáng, ngu n sáng phátệ ề ồ
đ ng th i hai ánh sáng đ n s c ồ ờ ơ ắ λ1, λ2 có b c sóng l n l t là 0,48 ướ ầ ượ µm và 0,60 µm. Trên
màn quan sát, trong kho ng gi a hai vân sáng g n nhau nh t và cùng màu v i vân sángả ữ ầ ấ ớ
v i vân sáng trung tâm cóớ
A. 4 vân sáng λ1 và 3 vân sáng λ2.B. 5 vân sáng λ1 và 4vân sáng λ2.
C. 4 vân sáng λ1 và 5vân sáng λ2.D. 3 vân sáng λ1 và 4vân sáng λ2.
GV: Lê Văn Long – DĐ: 0915714848 – Tr ng THPT Lê L iườ ợ
Cách 2: Mu n t i v trí nào đó có màu cùng v i màu c a vân trung tâm thì t i đó ph iố ạ ị ớ ủ ạ ả
là v trí trùng nhau c a 2 vân sáng c a 2 b c x . Do đó ị ủ ủ ứ ạ
1 2
1 1 2 2
2 1
5
4
k
k k k
λ
λ λ λ
= = =�
. Do
gi a vân trung tâm và ví trí trùng nhau đo không con vân sáng nào trùng nhau n a nênữ ữ
trong kho ng đó có 4 vân sáng c a ả ủ λ1 và 3 vân sáng λ2.
* Nh n xétậ : Cách 2 là cách gi i hay (nhanh, ít tính toán, đ n gi n).ả ơ ả
G i ý cách gi i ợ ả
Nh n xét:ậ Công su t nhà máy P và đi n tr đ ng dây R không đ i.ấ ệ ở ườ ổ
G i Pọ0 là công su t tiên th c a m t h dân. Ta cóấ ụ ủ ộ ộ
2
02
2
0 1 2
2
0 2 0 2
2
2
0 3
02
120
:120
2 :144 144 4
4 :
16
P
P R P
U
U P RI P P
U P RI P P R P
U
U nP RI P P
nP R P
U
+ =
+ =
+ = + =� �
� �
� �
+ =
+ =
2
02
2
02
3
24 4150.
15
( 120) 16
RP
PUn
RP
n P U
=
=�
− =
Có cách gi i khác nh ng th y th y cách này ng n nên th y ch ch n cách này.ả ư ầ ấ ắ ầ ỉ ọ
Có th có các cách gi i sau:ể ả
Cách 1
* Sau th i gian ờ
1( )
400 4
u
t s t
π
ϕ ω
∆ = ∆ = ∆ =
. Trên đ ngườ
tròn l n ng ớ ứ
u
M
.
* Giá tr i = 0 , đang gi m, trên đ ng tròn nh ng v i ị ả ườ ỏ ứ ớ
i
M
.
Câu 24 (mã đ ề 958 ): Đi n năng t m t tr m phát đi n đ c đ a đ n m t khu tái đ nh cệ ừ ộ ạ ệ ượ ư ế ộ ị ư
b ng đ ng dây truy n t i m t pha. Cho bi t, n u đi n áp t i đ u truy n đi tăng t Uằ ườ ề ả ộ ế ế ệ ạ ầ ề ừ
lên 2U thì s h dân đ c tr m cung c p đ đi n năng tăng t 120 lên 144. Cho r ng chiố ộ ượ ạ ấ ủ ệ ừ ằ
tính đ n hao phí trên đ ng dây, công su t tiêu th đi n c a các h dân đ u nh nhau,ế ườ ấ ụ ệ ủ ộ ề ư
công su t c a tr m phát không đ i và h s công su t trong các tr ng h p đ u b ngấ ủ ạ ổ ệ ố ấ ườ ợ ề ằ
nhau. N u đi n áp truy n đi là 4U thì tr m phát huy này cung c p đ đi n năng choế ệ ề ạ ấ ủ ệ
A. 168 h dân.ộB. 150 h dân.ộC. 504 h dân.ộD. 192 h dân.ộ
Câu 29 (mã đ ề 958 ): Đ t đi n áp u = 400cos100ặ ệ πt (u tính b ng V, t tính b ng s) vào haiằ ằ
đ u đo n m ch AB g m đi n tr thu n 50 ầ ạ ạ ồ ệ ở ầ Ω m c n i ti p v i đo n m ch X. C ng đắ ố ế ớ ạ ạ ườ ộ
dòng đi n hi u d ng qua đo n m ch là 2 A. Bi t th i đi m t, đi n áp t c th i gi a haiệ ệ ụ ạ ạ ế ở ờ ể ệ ứ ờ ữ
đ u AB có giá tr 400 V; th i đi m ầ ị ở ờ ể
1
400
t+
(s), c ng đ dòng đi n t c th i qua đo nườ ộ ệ ứ ờ ạ
m ch b ng không và đang gi m. Công su t tiêu th đi n c a đo n m ch X là ạ ằ ả ấ ụ ệ ủ ạ ạ
A. 400 W. B. 200 W. C. 160 W. D. 100 W.
π
/4
M
i
M
U
O