TR NG THPT H U L C 2ƯỜ Ậ Ộ Đ THI TH Đ I H C L N 1 - NĂM H C 2008 - 2009Ề Ử Ạ Ọ Ầ Ọ
Môn: TOÁN
Th i gian làm bài: 180 phút, không k th i gian phát đờ ể ờ ề
PH N CHUNG CHO T T C CÁC THÍ SINHẦ Ấ Ả
Câu I (2 đi m)ể
Cho hàm s ố
( ) ( )
3 2 2 2
y x 3mx 3 m 1 x m 1= − + − − −
(
m
là tham s ) (1).ố
1. Kh o sát s bi n thiên và v đ th c a hàm s (1) khi ả ự ế ẽ ồ ị ủ ố
m 0.
=
2. Tìm các giá tr c a m đ đ th hàm s (1) c t tr c hoành t i 3 đi m phân bi t có hoànhị ủ ể ồ ị ố ắ ụ ạ ể ệ
đ d ng .ộ ươ
Câu II (2 đi m)ể
1. Gi i ph ng trình: ả ươ
2sin 2x 4sin x 1 0.
6
π
� �
− + + =
� �
� �
2. Gi i h ph ng trình: ả ệ ươ
( )
( )
( )
( )
( )
2 2
2 2
x y x y 13 x, y .
x y x y 25
x− + =
−−
−+ − =
+
+
+
Câu III (1 đi m)ể
Cho hình chóp
S.ABCD
có đáy
ABCD
là hình ch nh t v i ữ ậ ớ
c nh ạ
SA
vuông góc v i đáy, c nh ớ ạ
SB
t o v i m t ph ng đáy m t góc ạ ớ ặ ẳ ộ
o
60 .
Trên c nh ạ
SA
l y đi mấ ể
M
sao cho
a 3
AM 3
=
. M t ph ng ặ ẳ
( )
BCM
c t c nh ắ ạ
SD
t i đi m ạ ể
N
. Tính th tích kh iể ố
chóp
S.BCNM.
Câu IV (2 đi m)ể
1. Tính tích phân:
6
2
dx
I2x 1 4x 1
=+ + +
+
2. Tìm giá tr l n nh t và giá tr nh nh t c a hàm s : y = 2sinị ớ ấ ị ỏ ấ ủ ố 8x + cos42x
PH N T CH N: Thí sinh ch n câu V.a ho c câu V.b Ầ Ự Ọ ọ ặ
Câu V.a.( 3 đi m ) ểTheo ch ng trình Chu nươ ẩ
1. Cho đ ng tròn (C) : ườ
( ) ( )
2 2
x 1 y 3 4− + − =
và đi m M(2;4) .ể
a) Vi t ph ng trình đ ng th ng đi qua M và c t đ ng tròn (C) t i hai đi m A, B saoế ươ ườ ẳ ắ ườ ạ ể
cho M là trung đi m c a AB ể ủ
b) Vi t ph ng trình các ti p tuy n c a đ ng tròn (C) có h s góc k = -1 .ế ươ ế ế ủ ườ ệ ố
2. Cho hai đ ng th ng song song dườ ẳ 1 và d2. Trên đ ng th ng dườ ẳ 1 có 10 đi m phân bi t, trên ể ệ
đ ng th ng dườ ẳ 2 có n đi m phân bi t (ể ệ
n 2n
). Bi t r ng có 2800 tam giác có đ nh là cácế ằ ỉ
đi m đã cho. Tìm n. ể
Câu V.b.( 3 đi m ) ểTheo ch ng trình Nâng caoươ
1. Áp d ng khai tri n nh th c Niut n c a ụ ể ị ứ ơ ủ
( )
100
2
x x+
, ch ng minh r ng:ứ ằ
99 100 198 199
0 1 99 100
100 100 100 100
1 1 1 1
100C 101C 199C 200C 0.
2 2 2 2
� � � � � � � �
− + − + =���
� � � � � � � �
� � � � � � � �
2. . Cho hai đưng tròn : (Cờ1) : x2 + y2 – 4x +2y – 4 = 0 và (C2) : x2 + y2 -10x -6y +30 = 0
có tâm l n l t là I, Jầ ượ
a) Ch ng minh (Cứ1) ti p xúc ngoài v i (Cế ớ 2) và tìm t a đ ti p đi m H .ọ ộ ế ể
b) G i (d) là m t ti p tuy n chung không đi qua H c a (Cọ ộ ế ế ủ 1) và (C2) . Tìm t a đ giao đi mọ ộ ể
K c a (d) và đ ng th ng IJ . Vi t ph ng trình đ ng tròn (C) đi qua K và ti p xúc v iủ ườ ẳ ế ươ ườ ế ớ
hai đ ng tròn (Cườ 1) và (C2) t i H .ạ
----------------------------- H t ế-----------------------------
Cán b coi thi không gi i thích gì thêm.ộ ả
trêng thpt hËu l éc 2
®¸p ¸n ®Ò thi thö ®¹ i häc l Çn 1 n¨m häc 2008 -
2009
M«n thi: to¸n
Thêi gian lµm bµi: 180 phót, kh«ng kÓ thêi
gian giao ®Ò
C©u Néi dung §iÓm
I
2.0®
1
1,25
®
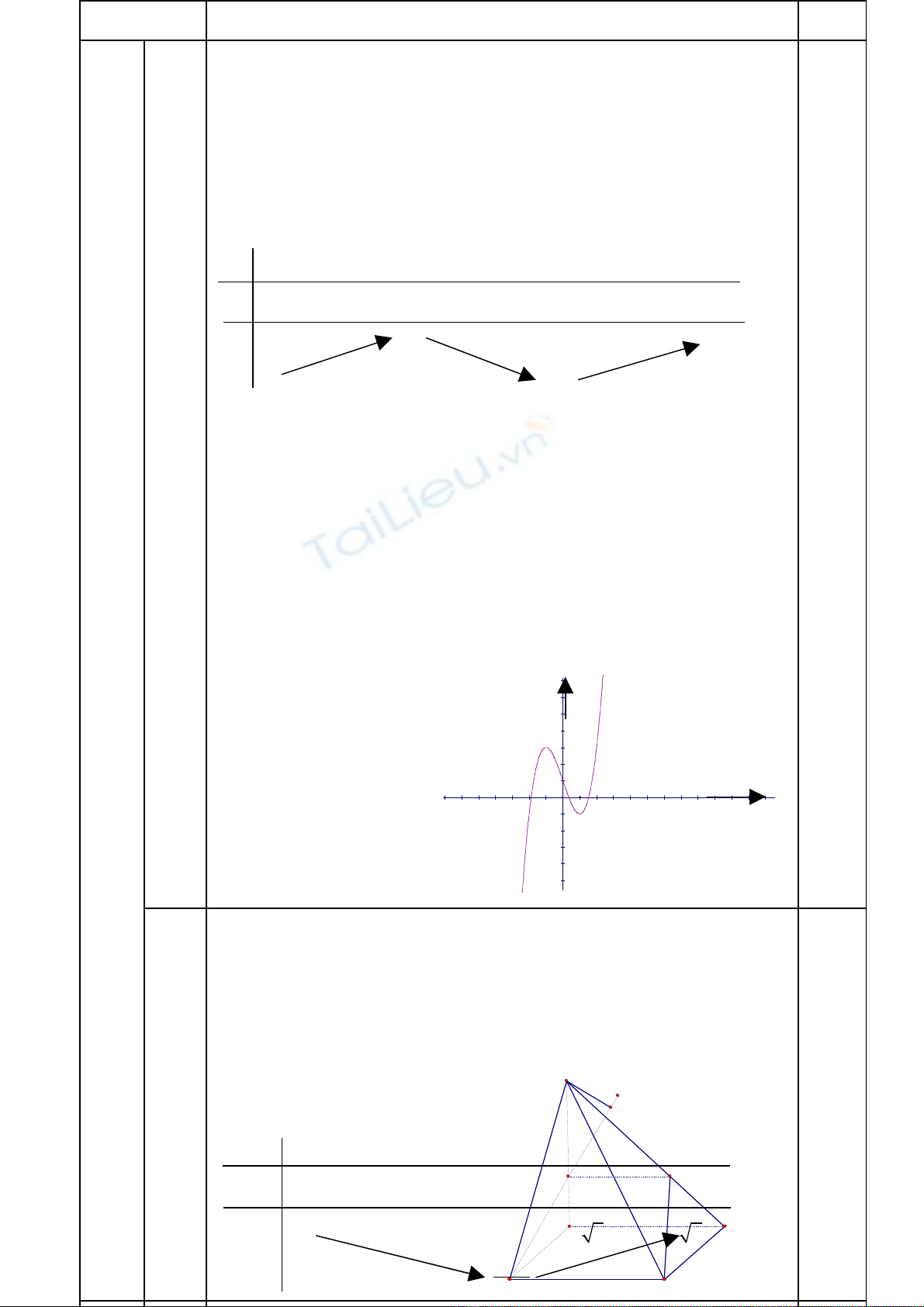
Víi m = 0 , ta cã :
y = x3 – 3x + 1
- TX§:
R
- Sù biÕn thiªn:
+ ) Giíi h¹n :
x x
Lim y ; Lim y
L−my +L
= −m= +L
+) B¶ng biÕn thiªn:
Ta cã : y’ = 3x2 – 3
y’ = 0
x = -1 hoÆc x = 1
Hµm sè ® ång biÕn trªn m çi kho¶ng
( )
; 1−1−
vµ
( )
1;+;
,
nghÞch biÕn trªn kho¶ng ( -1; 1)
Hµm sè ® ¹t cùc ® ¹i t¹i ®iÓm x = -1, gi¸ trÞ cùc ® ¹i
cña hµm sè lµ y(-1) = 3
Hµm sè ® ¹t cùc tiÓu t¹i ®iÓm x = 1, gi¸ trÞ cùc
tiÓu cña hµm sè lµ y(1) = -1
- §å thÞ
+ §iÓm uèn : Ta cã : y’’ = 6x , y" = 0 t¹i ®iÓm x =
0 vµ y" ®æ i dÊu tõ d¬ng sang ©m khi x qua ®iÓm x =
0 . VËy U(0 ; 1) lµ ®iÓm uèn cña ® å thÞ .
+ G iao ®iÓm víi trôc tung : (0 ;1)
+ §THS ®i qua c¸c ®iÓm :
A(2; 3) , B(1/2; -3/8)
C(-2; -1)
0,25
0,25
0,25
0,5
2
0.75
®
§Ó §THS (1) c¾t trôc hoµnh t¹i 3 ®iÓm ph©n biÖt cã
hoµnh ® é d¬ng, ta ph¶i cã :
( ) ( )
( )
1 2
y'
1
2
x x
0
x 0
x 0
y y 0
y 0 0
y>
>>
>
>>
>
><
<
<<
<
V
(I)
Trong ® ã : y’ = 3( x2 – 2mx + m2 – 1)
∆y’ = m2 – m2 + 1 = 1 > 0 víi mäi m
y’ = 0 khi x1 = m – 1 = xC§ vµ x2 = m + 1 = xCT .
(I)
( ) ( ) ( )
( )
2 2 2
2
m 1 0
m 1 0
3 m 1 2
m 1 m 3 m 2m 1 0
m 1 0
− >
−
−+ >
+< < +� �
�− − − − <
−
−− − <
−
0,25
0,5
Ta cã :
2sin 2x 4sin x 1 0.
6
π
� �
− + + =
� �
� �
y’
y
x
+’
−’
+
+’
−’
-1
+
00 -
1
3
-1
-
6
6
4
4
2
2
-2
2
-4
4
-5
5 5
5 10
y
x
x
N
N
D
D
B
BC
C
A
A
S
S
M
M
H
t
f’(t)
f(t)
-1 1/3 1
+
0
-
3
1
27
1