TNU Journal of Science and Technology
229(10): 456 - 466
http://jst.tnu.edu.vn 456 Email: jst@tnu.edu.vn
USING SECOND-ORDER CONE PROGRAMMING-BASED ITERATIVE
METHOD FOR LOAD FLOW ANALYSIS IN MESHED POWER
TRANSMISSION NETWORKS
Do Minh Hong, Pham Nang Van*, Nguyen Thi Hoai Thu
School of Electrical and Electronic Engineering - Hanoi University of Science and Technology
ARTICLE INFO
ABSTRACT
Received:
01/7/2024
Power transmission networks are often designed and operated as meshed
topologies. The power flow equations of these networks are nonlinear.
They are typically solved using iterative methods such as Newton-
Raphson. This research introduces an iterative method for analyzing power
flow in meshed power transmission networks using second-order cone
programming (SOCP). The proposed approach is extended from the SOCP
procedure for radial electrical networks by adding constraints for the
voltage phase angle on each branch in the transmission network.
Simultaneously, the proposed SOCP method integrates the power flow
equations into optimization problems. Therefore, optimization formulation
using the proposed SOCP model is convex, and the globally optimal
solution is attained. The proposed SOCP model is evaluated on a power
transmission network with six buses and IEEE thirty buses using the
GAMS programming language and the CPLEX commercial software. The
computational results indicate that, in comparison to the standard Newton-
Raphson approach, the solution of the suggested methodology has a very
small error, which can be entirely disregarded in real-world applications.
Revised:
01/8/2024
Published:
01/8/2024
KEYWORDS
Power transmission networks
Meshed power networks
Load flow analysis
Second-order cone
programming (SOCP)
Optimization methods
SỬ DỤNG PHƢƠNG PHÁP LẶP DỰA TRÊN QUY HOẠCH NÓN BẬC HAI
ĐỂ PHÂN TÍCH CHẾ ĐỘ XÁC LẬP CỦA LƢỚI ĐIỆN TRUYỀN TẢI
CÓ MẠCH VÕNG KÍN
Đỗ Minh Hồng, Phạm Năng Văn*, Nguyễn Thị Hoài Thu
Trường Điện ‒ Điện tử, Đại học Bách khoa Hà Nội
TÓM TẮT
Ngày nhận bài:
01/7/2024
Lưới điện truyền tải thường được thiết kế và vận hành với cấu trúc mạch
vòng kín. Hệ phương trình cân bằng công suất của lưới điện này là không
tuyến tính và thường được giải sử dụng các phương pháp lặp như
Newton-Raphson. Bài báo này đề xuất phương pháp lặp sử dụng quy
hoạch hình nón bậc hai (SOCP) nhằm xác định điện áp nút và dòng công
suất của lưới điện truyền tải trong chế độ xác lập. Phương pháp đề xuất
được mở rộng từ phương pháp SOCP cho lưới điện hình tia bằng cách bổ
sung ràng buộc về góc pha điện áp cho mỗi nhánh trong lưới điện truyền
tải. Đồng thời, phương pháp SOCP đề xuất giúp tích hợp hệ phương trình
cân bằng công suất vào các bài toán tối ưu hóa trong hệ thống điện. Các
bài toán tối ưu này có dạng lồi và đảm bảo tìm được nghiệm tối ưu toàn
cục. Phương pháp lặp đề xuất được đánh giá trên lưới điện truyền tải 6
nút và 30 nút IEEE sử dụng ngôn ngữ lập trình GAMS/CPLEX. Các kết
quả tính toán cho thấy phương pháp lặp đề xuất có sai số rất nhỏ so với
phương pháp Newton-Raphson chuẩn và sai số này hoàn toàn có thể
được bỏ qua trong các áp dụng thực tế.
Ngày hoàn thiện:
01/8/2024
Ngày đăng:
01/8/2024
DOI: https://doi.org/10.34238/tnu-jst.10686
* Corresponding author. Email: van.phamnang@hust.edu.vn
TNU Journal of Science and Technology
229(10): 456 - 466
http://jst.tnu.edu.vn 457 Email: jst@tnu.edu.vn
1. Giới thiệu
Lưới điện truyền tải có nhiệm vụ truyền tải điện năng từ các trung tâm sản xuất điện đến các
khu vực tiêu thụ và được coi là ―xương sống‖ của mạng lưới điện. Lưới điện này thường có cấu
trúc mạch vòng kín nhằm nâng cao độ tin cậy cung cấp điện. Ngày nay, mức độ thâm nhập ngày
càng tăng các nguồn năng lượng mới và tái tạo cùng với sự gia tăng không ngừng của phụ tải dẫn
đến sự phức tạp trong công tác quy hoạch và vận hành lưới điện này. Quy hoạch và vận hành lưới
điện truyền tải là các bài toán tối ưu phức tạp. Một trong những ràng buộc của bài toán tối ưu này
là hệ phương trình cân bằng công suất nút. Do tính phi tuyến của hệ phương trình này nên không
đảm bảo tìm được nghiệm tối ưu toàn cục của các bài toán tối ưu. Bài toán phân tích chế độ xác
lập của lưới điện và các phương pháp toán học nhằm tích hợp hệ phương trình này vào các mô
hình tối ưu đã được nghiên cứu trong một số bài báo.
Phân tích chế độ xác lập của lưới điện thường được thực hiện bằng các phương pháp lặp như
phương pháp Gauss-Seidel [1] hoặc phương pháp Newton-Raphson [2]. Đặc tính hội tụ của
phương pháp Gauss-Seidel có dạng tuyến tính và cần nhiều thời gian khi tính toán cho các lưới
điện có kích cỡ lớn. Phương pháp Newton-Raphson (NR) tính toán ở dạng số thực và có đặc tính
hội tụ bậc hai. Tuy nhiên, các tác giả [3] chỉ ra rằng phương pháp này không tìm được nghiệm
trong một số trường hợp như lưới điện có tỷ số R/X lớn. Ngoài ra, phương pháp NR không phù
hợp trong các áp dụng thời gian thực do không đáp ứng về mặt thời gian tính toán. Do đó, các tác
giả trong [4] đã đề xuất phương pháp tách biến nhanh (Fast Decoupled Power Flow ‒ FDPF).
Phương pháp này được phát triển từ phương pháp NR với mục đích cải thiện thời gian tính toán.
Phương pháp FDPF xem xét mối liên hệ yếu giữa công suất tác dụng và mô-đun điện áp, công
suất phản kháng và góc pha điện áp. Đồng thời, ma trận Jacobi được coi là hằng số khi tính toán
với phương pháp FDPF. Tuy nhiên, kỹ thuật này không thể áp dụng với các lưới điện mang tải
nặng hoặc điện áp định mức dưới 220 kV. Với sự phi điều tiết trong lĩnh vực điện và xây dựng
thị trường mua bán điện năng, phương pháp trào lưu công suất một chiều (Direct Current Power
Flow ‒ DCPF) đang ngày càng được quan tâm [5], [6]. Hệ phương trình cân bằng công suất theo
phương pháp DCPF có dạng tuyến tính và chỉ góc pha điện áp là các biến cần tìm. Nghiên cứu
[7] áp dụng phương trình trào lưu công suất một chiều có xét tổn thất công suất tác dụng cho bài
toán quy hoạch mở rộng mạng điện truyền tải. Tuy nhiên, phương pháp trào lưu công suất tuyến
tính không xét vấn đề điện áp trong hệ thống điện. Các bài báo [8], [9] áp dụng mô hình quy
hoạch hình nón bậc hai (SOCP) trong các bài toán phân tích trào lưu công suất, trào lưu công suất
tối ưu và ổn định điện áp của hệ thống điện. Bài báo [10] áp dụng mô hình SOCP để xác định
dòng công suất cho lưới điện hình tia có tích hợp các nguồn điện phân tán. Tuy nhiên, nghiên cứu
[10] chưa xét trường hợp lưới điện có mạch vòng kín, đặc biệt là lưới điện truyền tải thường có
nhiều mạch vòng kín.
Bài báo này có mục đích xây dựng phương pháp lặp dựa trên mô hình SOCP để phân tích chế
độ xác lập của lưới điện truyền tải có mạch vòng kín. Các đóng góp của bài báo này bao gồm:
Đề xuất phương pháp lặp dựa trên mô hình SOCP để giải bài toán phân tích chế độ xác lập
của lưới điện truyền tải.
So sánh kết quả tính toán của kỹ thuật lặp đề xuất với phương pháp Newton-Raphson.
Bài báo có cấu trúc gồm bốn phần. Phần 1 giới thiệu tổng quan về nội dung nghiên cứu. Cơ sở
lý thuyết của phương pháp đề xuất được trình bày ở phần 2. Phần 3 trình bày kết quả nghiên cứu
cho lưới điện truyền tải 6 nút. Phần 4 trình bày các kết luận và hướng nghiên cứu trong tương lai.
2. Cơ sở lý thuyết
2.1. Mô hình quy hoạch hình nón bậc hai
Xét lưới điện truyền tải hai nút có sơ đồ thay thế được mô tả trong Hình 1.
TNU Journal of Science and Technology
229(10): 456 - 466
http://jst.tnu.edu.vn 458 Email: jst@tnu.edu.vn
1
2
sh
ik
jb
1
2
sh
ik
jb
ii
V
kk
V
i
k
ik ik
r jx
H nh 1. Sơ đồ thay thế của lưới điện truyền tải
hai nút [11]
Dòng công suất trên nhánh ik tại nút i được
tính toán như sau:
2cos sin
ik ik i i k ik ik ik ik
P g V VV g b

(1)
2sin cos
2
sh
ik
ik ik i i k ik ik ik ik
b
Q b V VV g b




(2)
trong đó:
và
ik ik
PQ
lần lượt là dòng công suất tác dụng và phản kháng trên nhánh ik tại nút i;
và
ik ik
gb
lần lượt là phần thực và ảo của tổng dẫn dọc nhánh ik;
2 2 2 2
;
ik ik
ik ik
ik ik ik ik
rx
gb
r x r x

(3)
sh
ik
b
là phần ảo của tổng dẫn ngang nhánh ik;
và
ik
VV
lần lượt là mô-đun điện áp tại nút i và k;
ik
là sự chênh lệch góc pha điện áp giữa hai nút i và k.
Với lưới điện truyền tải có N nút, ta giả sử tổng số nút PQ là
D
N
thì số nút PV (trừ nút cân
bằng) là
GD
1.N N N
Hệ phương trình mô tả lưới điện truyền tải có N nút trong chế độ xác
lập được viết như sau:
2
G D D G
1,k 1,k
cos sin ;
NN
ik ik i i k ik ik ik ik i i
k i k i
P g V VV g b P P i N N


(4)
2
G D D
1,k 1,k
sin cos ;
2
sh
NN
ik
ik ik i i k ik ik ik ik i i
k i k i
b
Q b V VV g b Q Q i N





(5)
trong đó,
GG
và
ii
PQ
lần lượt là công suất tác dụng và phản kháng của nguồn điện tại nút i;
DD
và
ii
PQ
lần lượt là công suất tác dụng và phản kháng của phụ tải tại nút i.
Biểu thức (4) và (5) mô tả
DG
2NN
phương trình với tổng số biến
,
ii
V
là
DG
2NN
. Tuy
nhiên, hệ phương trình trên là phi tuyến. Đặt
2, cos
i i ik i k ik
v V c VV

và
sin
ik i k ik
s VV
, hệ
phương trình (4)-(5) được viết lại như sau:
G D D G
1,k 1,k
;
NN
ik ik i ik ik ik ik i i
k i k i
P g v g c b s P P i N N

(6)
G D D
1,k 1,k
;
2
sh
NN
ik
ik ik i ik ik ik ik i i
k i k i
b
Q b v g s b c Q Q i N




(7)
Do
và
ik ki ik ki
c c s s
nên phương trình (6) và (7) biểu diễn
DG
2NN
phương trình tuyến
tính với tổng số biến
, , ,
i i ik ik
v c s
là
DG
22N N L
. Bên cạnh đó, 2L phương trình được biểu
diễn qua mối liên hệ giữa
, và
ik ik ik
cs
cho mỗi nhánh ik:
22
L
;
i k ik ik
v v c s ik
(8)
L
arctan ;
ik
ik
ik
sik
c




(9)
trong đó, L là tổng số nhánh của mạng điện truyền tải;
L
là tập các nhánh của lưới điện
truyền tải;
i
là góc pha điện áp nút i và
k
là góc pha điện áp nút k.
Biểu thức (8) là ràng buộc không lồi. Do đó, biểu thức này được biến đổi về dạng hình nón:
22
L
;
i k ik ik
v v c s ik
(10)
TNU Journal of Science and Technology
229(10): 456 - 466
http://jst.tnu.edu.vn 459 Email: jst@tnu.edu.vn
Khi đó, bài toán phân tích chế độ xác lập (6), (7) và (10) có dạng hình nón và có thể được giải
sử dụng quy hoạch toán học. Tuy nhiên, các biểu thức (6), (7) và (10) chỉ đúng cho lưới điện hình
tia. Do lưới điện truyền tải thường có cấu trúc mạch vòng kín nên (6), (7) và (10) không đảm bảo
rằng tổng chênh lệch góc pha điện áp cho mỗi vòng kín bằng 0. Do đó, biểu thức (9) được bổ
sung vào mô hình nón bậc hai cho lưới điện có mạch vòng kín. Vì hàm arctan là hàm không lồi
nên các tác giả đề xuất biến đổi (9) thành dạng tuyến tính bằng cách áp dụng khai triển Taylor.
( ) ( ) ( )
L
( ) 2 2
( ) ( )
arctan ;
r r r
ik ik ik ik ik
ik
rrr
ik ik ik
s s c c s ik
csc




(11)
trong đó,
( ) ( )
và
rr
ik ik
sc
là các giá trị xấp xỉ của
và
ik ik
cs
ở bước lặp thứ r.
2.2. Phân tích chế độ xác lập của lưới điện truyền tải sử dụng phương pháp lặp dựa trên quy
hoạch hình nón bậc hai
Để bắt đầu quá trình lặp, xấp xỉ đầu của các biến
và
ik ik
cs
được lựa chọn như sau:
(0) (0)
1 và 0.
ik ik
cs
Sự lựa chọn xấp xỉ này phản ánh sự thật rằng mô-đun điện áp lệch rất ít so với 1
pu
1 pu
ik
VV
và chênh lệch góc pha điện áp giữa hai nút liền kề cũng rất nhỏ
ik

khi hệ
thống điện vận hành ở chế độ xác lập. Các trị số xấp xỉ này phù hợp tốt với tất cả các lưới điện vận
hành ở trạng thái xác lập và thuật toán hội tụ thường sau 3 bước lặp. Nhấn mạnh rằng, thuật toán có
thể không hội tụ hoặc hội tụ rất chậm nếu các trị số xấp xỉ đầu không được lựa chọn phù hợp.
Giả sử rằng ta đã biết các giá trị
( ) ( )
và
rr
ik ik
sc
ở bước lặp thứ r, mô hình quy hoạch hình nón bậc
hai (SOCP) để tính toán các giá trị ở bước lặp (r+1) được mô tả như sau:
L
max ik
ik
c

(12)
thỏa mãn các điều kiện:
G D D G
1,k 1,k
;
NN
ik ik i ik ik ik ik i i
k i k i
P g v g c b s P P i N N

(13)
G D D
1,k 1,k
;
2
sh
NN
ik
ik ik i ik ik ik ik i i
k i k i
b
Q b v g s b c Q Q i N




(14)
22
L
;
i k ik ik
v v c s ik
(15)
( ) ( ) ( )
L
2 2 ( )
( ) ( )
arctan ;
r r r
ik ik ik ik ik
ik r
rr ik
ik ik
s c c s s ik
c
sc




(16)
L
0;
ik
c ik
(17)
L
;;
ik ki ik ki
c c s s ik
(18)
D
0;
i
v i N
(19)
2
G
;
ii
v V i N
(20)
2; 0;
i i i
v V i ref
(21)
Thuật toán lặp dựa trên mô hình SOCP để tính toán chế độ xác lập của mạng điện truyền tải
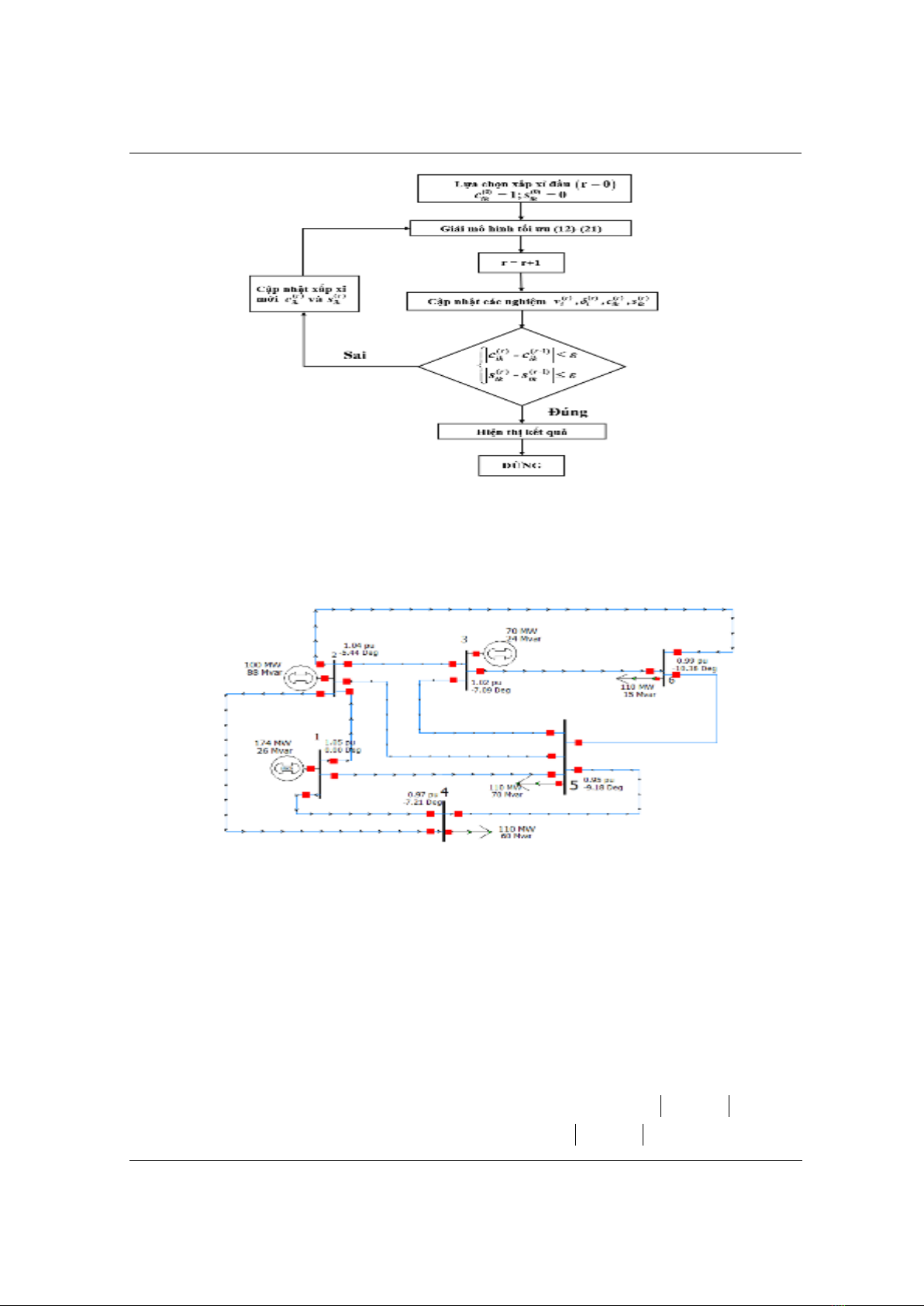
có mạch vòng kín gồm các bước như sau (xem Hình 2):
Bƣớc 0: Bắt đầu đếm chỉ số bước lặp
0r
. Lựa chọn xấp xỉ ban đầu là
(0) (0)
1; 0
ik ik
cs
.
Bƣớc 1: Giải mô hình nón bậc hai (12)-(21). Tăng chỉ số bước lặp r lên 1, biểu diễn các
nghiệm của mô hình tối ưu
( ) ( ) ( ) ( )
, , ,
r r r r
i i ik ik
v c s
.
Bƣớc 2: Kiểm tra điều kiện hội tụ. Nếu
( ) ( 1) ( ) ( 1)
và
r r r r
ik ik ik ik
c c s s


đều nhỏ hơn hoặc bằng
6
10
thì thuật toán dừng và in ra các nghiệm. Nếu không thì cập nhật các xấp xỉ mới
( ) ( )
và
rr
ik ik
cs
và
quay lại Bước 1.
TNU Journal of Science and Technology
229(10): 456 - 466
http://jst.tnu.edu.vn 460 Email: jst@tnu.edu.vn
H nh 2. Lưu đồ thuật toán đề xuất
3. Kết quả nghiên cứu
Mục này trình bày kết quả tính toán chế độ xác lập của lưới điện truyền tải 6 nút và 30 nút
IEEE [12] sử dụng phương pháp lặp dựa trên mô hình SOCP. Hình 3 mô tả sơ đồ lưới điện truyền
tải 6 nút trên phần mềm POWERWORLD [13].
H nh 3. Tính toán trào lưu công suất bằng phần mềm POWERWORLD
Mô hình tối ưu dựa trên quy hoạch hình nón bậc hai được giải bằng bộ giải thương mại
GAMS/CPLEX [14] trên máy tính Intel Core i5-6300HQ 2,3-GHz, 8 GB RAM. Kết quả tính
toán của kỹ thuật đề xuất được so sánh với phương pháp Newton-Raphson truyền thống.
3.1. Lưới điện 6 nút
3.1.1. Dữ liệu tính toán
Bảng 1 và Bảng 2 trình bày thông số đường dây và dữ liệu tại các nút của lưới điện truyền tải
6 nút. Điện áp danh định của mạng điện 6 nút là 230 kV. Điện áp tại nút cân bằng là 1,05 pu (nút
1). Tất cả các dữ liệu được mô tả trong hệ đơn vị tương đối với công suất cơ bản bằng 100 MVA.
3.1.2. Kết quả tính toán
Phương pháp lặp dựa trên mô hình tối ưu SOCP hội tụ với 3 bước lặp. Bảng 3 mô tả giá trị
,
ik ik
cs
ở bước lặp thứ nhất. Đồng thời, kết quả bước lặp thứ nhất cho thấy
( ) ( 1)rr
ik ik
cc
có giá trị
lớn nhất là 0,0875 pu (tại nhánh 1-2 và lớn hơn 10-6 pu) và
( ) ( 1)rr
ik ik
ss
có giá trị lớn nhất là