Giaïo trçnh QUI HOAÛCH THUÍY LÅÜI ThS. Lã Anh Tuáún
----------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------
Chæång 4: LÆÛA CHOÜN PHÆÅNG AÏN ÂÁÖU TÆ
66
PHUÛ CHÆÅNG 4
QUI HOAÛCH TUYÃÚN TÊNH
--- oOo ---
Mäüt trong caïc phæång phaïp choün phæång aïn täúi æu, thuáût toaïn Qui hoaûch Tuyãún
tênh (Linear Programming) âæåüc sæí duûng nhiãöu trong phán têch kinh tãú. Sau âáy laì
caïc vê duû dáùn âãún caïc baìi toaïn Quy hoaûch Tuyãún tênh:
Vê duû thæï 1:
Näng dán Hai Luïa coï 50 ha âáút. Bãn caûnh kyî thuáût kinh nghiãûm canh taïc vaì tiãn
âoaïn thë træåìng tiãu thuû, dæûa vaìo âiãöu kiãûn âáút âai, nhán læûc vaì nguäön næåïc, Hai
Luïa quyãút âënh träöng 2 loaûi hoa maìu laì Bàõp vaì Âáûu. Säø tay Träöng troüt cuía Hai Luïa
cho biãút âãø coï 1 Táún saín pháøm tæìng loaûi hoa maìu thç cáön:
Hoa maìu Yãúu täú
saín xuáút
Âån vë
tênh Bàõp (1) Âáûu (2)
Nguäön taìi
nguyãn låïn nháút
Âáút âai
Nhán læûc
Nguäön næåïc
Ha/Táún
Ngæåìi - Vuû/Táún
10
6
m
3
/ Táún
2
6
20
3
4
5
50 Ha
90 Ngæåìi - Vuû
250 x 10
6
m
3
Tiãön låìi Tr.Â/ Táún 18 21
Haîy âënh phæång aïn huy âäüng nguäön taìi nguyãn âãø coï säú saín pháøm baïn låìi nháút.
Hæåïng giaíi:
Goüi X
1
laì säú táún thu hoaûch cho vuû Bàõp, X
2
laì säú táún thu hoaûch cho vuû Âáûu.
Giaï baïn cho säú saín pháøm naìy:
Z = 18.X
1
+ 21.X
2
(täøng låüi nhuáûn thu âæåüc theo phæång aïn saín xuáút)
Muûc tiãu cuía Hai Luïa laì coï giaï trë Zmax.
Goüi Z =
n
j
jj
XC
1
max. Z goüi laì haìm muûc tiãu (Objective Function).
trong âoï Cj laì låüi nhuáûn thu âæåüc cho 1 âån vë saím pháøm Xj . Trong baìi toaïn trãn,
giaï trë X
1
vaì X
2
bë raìng buäüc båíi caïc yãúu täú khaïc (yãúu täú haûn chãú taìi nguyãn):
Âáút âai (i=1): 2X
1
+ 3X
2
50 (ha)
Nhán læûc (i=2): 6X
1
+ 4X
2
90 (ngæåìi - vuû)
Nguäön næåïc (i=3): 20X
1
+ 5X
2
250 (10
6
m
3
)
Täøng quaït:
n
j
ijij
bXa
1
, våïi i = 1 .. m, j = 1 .. n
Caïc raìng buäüc naìy goüi laì caïc raìng buäüc chuí âäüng (Active Constrains)
Dé nhiãn, X
1
vaì X
2
biãøu thë saín pháøm nãn: X
1
0 vaì X
2
0
hay Xj 0 våïi j = 1 .. m
Goüi laì caïc raìng buäüc thuû âäüng (Inactive Constrains)
Giaïo trçnh QUI HOAÛCH THUÍY LÅÜI ThS. Lã Anh Tuáún
----------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------
Chæång 4: LÆÛA CHOÜN PHÆÅNG AÏN ÂÁÖU TÆ
67
Toïm laûi ta coï baìi toaïn täøng quaït:
Z =
n
jjj XC
1
max
n
j
ijij
bXa
1
, våïi i = 1 .. m, j = 1 .. n
Xj 0
Hãû phæång trçnh daûng naìy goüi laì baìi toaïn Qui hoaûch Tuyãún tênh daûng Chuáøn.
Vê duû thæï 2:
Coï 3 häö chæïa næåïc A, B vaì C, nãúu muäún khai thaïc coï låüi thç læåüng næåïc láúy âi phaíi
êt nháút láön læåüt laì 20, 30, vaì 50 Triãûu m
3
trong muìa khä. Hai huyãûn I vaì II coï nhu
cáöu næåïc täúi thiãøu âãø canh taïc trong muìa khä láön læåüt laì 40 vaì 60 Triãûu m
3
.
Chi phê khai thaïc næåïc cho åí baíng sau:
Chi phê khai thaïc næåïc (10
6
$/ Triãûu m
3
) Huyãûn
A (20 Triãûu m
3
) B (30 Triãûu m
3
) C (50 Triãûu m
3
)
I
II
2
3
4
6
5
7
Haîy âënh phæång aïn khai thaïc næåïc våïi chi phê nhoí nháút.
Hæåïng giaíi:
Goüi X
1
, X
2
vaì X
3
laì khäúi læåüng næåïc tæì häö A, B vaì C vãö huyãûn I.
X
4
, X
5
vaì X
6
laì khäúi læåüng næåïc tæì häö A, B vaì C vãö huyãûn II.
Dé nhiãn, X
1
, X
2
, X
3
, X
4
, X
5
vaì X
6
0
Täøng kinh phê khai thaïc nguäön næåïc phaíi nhoí nháút, nghéa laì:
Z = 2X
1
+ 4X
2
+ 5X
3
+ 3X
4
+ 6X
5
+7X
6
min
Âãø âaím baío nhu cáöu næåïc täúi thiãøu cho mäùi huyãûn, ta coï:
X
1
+ X
2
+ X
3
40 (huyãûn I)
X
4
+ X
5
+ X
6
60 (huyãûn II)
Mæïc khai thaïc næåïc täúi thiãøu coï låüi cho tæìng häö chæïa:
Häö A: X
1
+ X
4
20 (Triãûu m
3
)
Häö B: X
2
+ X
5
30 (Triãûu m
3
)
Häö C: X
3
+ X
6
50 (Triãûu m
3
)
Giaïo trçnh QUI HOAÛCH THUÍY LÅÜI ThS. Lã Anh Tuáún
----------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------
Chæång 4: LÆÛA CHOÜN PHÆÅNG AÏN ÂÁÖU TÆ
68
Täøng quaït (theo caïc kyï hiãûu trãn):
Z =
n
jjj XC
1
min
n
j
ijij
bXa
1
, våïi i = 1 .. m, j = 1 .. n
Xj 0
Daûng naìy goüi laì baìi toaïn Qui hoaûch Tuyãún tênh daûng Cå baín.
Trong træåìng håüp:
Z =
n
j
jj
XC
1
min
n
jijij
bXa
1
, våïi i = 1 .. m, j = 1 .. n
Xj 0
Daûng naìy goüi laì baìi toaïn Qui hoaûch Tuyãún tênh daûng Chênh tàõc.
Daûng täøng quaït chung:
Z =
n
j
jj
XC
1
max (min)
n
j
jij
Xa
1
b
i
, våïi i = 1 .. m, j = 1 .. n
Xj 0 hoàûc khäng haûn chãú
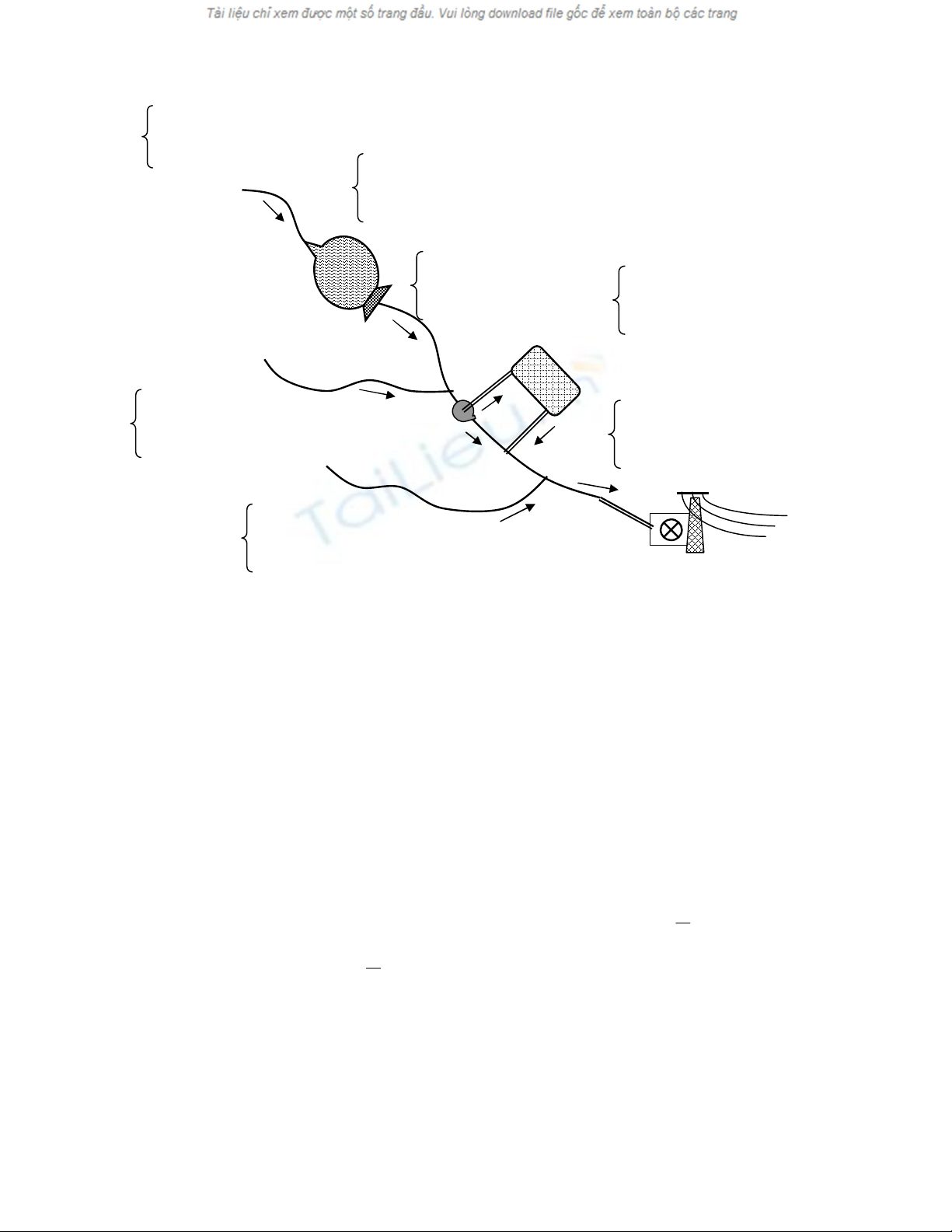
Vê duû: Mäüt hãû thäúng thuíy låüi nhæ hçnh veî, caïc dæî liãûu liãn quan âãún diãùn biãún cuía
cuía nguäön næåïc (âån vë laì triãûu m
3
) âæåüc xaïc âënh theo cå såí trung bçnh theo muìa
nhæ sau:
t =1 : Muìa xuán; t = 2 : Muìa haû;
t = 3 : Muìa thu; t = 4 : Muìa âäng.
Âiãöu kiãûn baìi toaïn:
Doìng chaíy âãún häö chæïa vaì doìng bäø xung hàòng nàm laì äøn âënh (thæûc tãú coï thãø
xeït theo táön suáút xuáút hiãûn)
Thåìi gian xeït laì 1 nàm thuíy vàn (tæì âáöu muìa xuán âãún cuäúi muìa âäng)
=
=
Giaïo trçnh QUI HOAÛCH THUÍY LÅÜI ThS. Lã Anh Tuáún
----------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------
Chæång 4: LÆÛA CHOÜN PHÆÅNG AÏN ÂÁÖU TÆ
69
Caïc biãún quyãút âënh:
K : dung têch häö chæïa
I : læåüng næåïc tæåïi cho näng trang/ nàm
E : håüp âäöng cung cáúp âiãûn
R
t
: læåüng næåïc xaí tæì häö nhàòm baío âaím doìng chaíy haû læu (cho giao
thäng, thuíy saín, caïc hoaût âäüng khaïc, ... )
S
t
: læåüng næåïc træî trong häö.
Haìm phaït âiãûn: E
t
= 0,144 Q
t
Q
t
: læåüng næåïc chaíy qua turbine åí muìa t
E
t
: nàng læåüng phaït ra åí muìa t
Viãûc saín xuáút nàng læåüng phaíi âæåüc phán bäú âãöu hàòng nàm:
4
E
E
t
Nàng luåüng thæìa:
)
4
(E
E
t
seî duìng båm næåïc tråí laûi häö.
Haìm muûc tiãu:
Tiãön låìi baïn âiãûn: 200 $/KWH/nàm
Tiãön tæåïi næåïc: 40 $/10
6
.m
3
/nàm
Tiãön baío dæåîng häö chæïa: 24 $/10
6
.m
3
/nàm
Læåüng xaí :
R
1
= 1,99 R
2
= 2,5
R
3
= 0,41 R
4
= 0,4
Näng trang
Nhu cáöu næåïc I (10
6
m
3
/nàm)
Häö chæïa næåïc coï
dung têch laì K,
læåüng træî laì S
t
Tæåïi
Læåüng træî tr
ong häö :
S
1
= 0,79 S
2
= 2,20
S
3
= 0 S
4
= 0,09
Læåüng næåïc âãún :
Z
11
= 0,4 Z
12
= 0,3
Z
13
= 0,5 S
14
= 1,1
Säng 1 bäø xung :
Z
21
= 0,79 S
22
= 2,20
Z
23
= 0 S
24
= 0,09
Säng 2 bäø xung :
Z
31
= 0,3 S
32
= 0,3
Z
33
= 0,6 S
34
= 1,3
Læåüng tæåïi:
K
1I
= 0,5.I K
2I
= 0,375.I
K
3I
= 0 K
4I
= 0,125.I
Læåüng næåïc traí vãö :
K’
1I
= 0,18.I K’
2I
= 0,12.I
K’
3I
= 0,12 K’
4I
= 0,08.I
Giaïo trçnh QUI HOAÛCH THUÍY LÅÜI ThS. Lã Anh Tuáún
----------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------
Chæång 4: LÆÛA CHOÜN PHÆÅNG AÏN ÂÁÖU TÆ
70
Giaíi:
Haìm muûc tiãu:
max Z = 200 E + 40 I - 24 K
Raìng buäüc:
Læåüng næåïc xaí:
R
t
S
t
+ Z
1t
våïi t = 1 .. 4
Cán bàòng næåïc häö chæïa:
St = St-1 + Z
1
t-1
- R
t-1
(xem læåüng bäúc håi vaì roì rè khäng âaïng kãø)
ÅÍ muìa xuán, t = 1, cho S
t-1
= S
4
(cuía nàm træåïc)
Dung têch häö chæïa:
S
t
+ Z
1t
- R
t
K
Doìng chaíy åí âiãøm láúy næåïc tæåïi:
Z
2t
+ R
t
- K
tI
0 våïi t = 1 .. 4
Læåüng næåïc cho nhaì maïy thuíy âiãûn phaíi låïn hån læåüng næåïc cáön thiãút cho
maïy chaûy:
Z
2t
+ R
t
- K
t
.I + K'
t
.I + Z
3t
144,04
E
våïi t = 1 .. 4
Caïc raìng buäüc thuû âäüng:
S
t
, R
t
, E, I vaì K 0
Caïc baìi toaïn qui hoaûch tuyãún tênh coï thãø giaíi bàòng caïc phæång phaïp sau:
Phæång phaïp âäö giaíi (Graphical method)
Phæång phaïp âån hçnh (Simplex method)
Phæång phaïp âäúi ngáùu (Dual method)
Hiãûn nay, coï ráút chæång trçnh maïy tênh âaî âæåüc láûp sàôn âãø giuïp viãûc giaíi caïc baìi
toaïn qui hoaûch tuyãún tênh, vê duû nhæ pháön mãöm QSB (Quantitative Systems for
Bussiness) cuía taïc giaí Yih-Long Chang vaì Robert S. Sullian, 1986.