Sáng kiến kinh nghiệm môn vật lý năm học 2018 - 2019
Giáo viên: Lê Thị Hiệp – Trường THCS Lương Thế Vinh Trang 1
MỤC LỤC
I. Phần mở đầu: ...................................................................................................2
1. Lý do chọn đề tài...............................................................................2
2. Mục tiêu, nhiệm vụ của đề tài. ..........................................................2
3. Đối tượng nghiên cứu........................................................................3
4. Giới hạn của đề tài............................................................3
5. Phương pháp nghiên cứu. .................................................................3
II. Phần nội dung ...................................................................... .........................3
1. Cơ sở lý luận.................................................................. 3
2.Thực trạng vấn đề nghiên cứu........................................ ...... 4
3. Nội dung và hình thức của giải pháp, biện pháp:.........................................4
a. Mục tiêu của giải pháp..........................................................5
b. Nội dung và cách thức thực hiện giải pháp...........................5
c. Mối quan hệ giữa các giải pháp, biện pháp.............. ............................14
d. Kết quả khảo nghiệm, giá trị khoa học của vấn đề nghiên cứu ……....14
III. Phần kết luận, kiến nghị ......................................... ..................................14
1. Kết luận: ......................................... .........................................................15
2.Kiến nghị: ......................................... .......................................................15
Tài liệu tham khảo ……………………………………………………………..16
Sáng kiến kinh nghiệm môn vật lý năm học 2018 - 2019
Giáo viên: Lê Thị Hiệp – Trường THCS Lương Thế Vinh Trang 2
BỒI DƯỠNG HỌC SINH GIỎI VỚI BÀI TOÁN ‘CỰC TRỊ’
TRONG VẬT LÝ
I. Phần mở đầu:
1. Lý do chọn đề tài.
Đảng ta chủ trương đẩy mạnh công tác giáo dục, và coi đây là một trong những yếu
tố đầu tiên, yếu tố quan trọng góp phần phát triển kinh tế - xã hội. Mục tiêu của giáo dục
là: “Nâng cao dân trí, đào tạo nhân lực và bồi dưỡng nhân tài”.
Bồi dưỡng nhân tài cho đất nước là một trong những nhiệm vụ của ngành giáo dục,
xem trọng “Hiền tài là nguyên khí của quốc gia” công tác bồi dưỡng học sinh giỏi ở các
trường THCS hiện nay đã được tổ chức thực hiện trong nhưng năm qua. Bồi dưỡng học
sinh giỏi là nhiệm vụ then chốt trong mỗi nhà trường, là thành quả để tạo lòng tin với
phụ huynh và là cơ sở tốt để xã hội hoá giáo dục.
Trong việc nâng cao chất lượng giáo dục và bồi dưỡng học sinh giỏi. Việc cải tiến
phương pháp học là rất quang trọng, bên cạnh việc bồi dưỡng kiến thức chuyên môn việc
phát huy yếu tố tích cực của học sinh hết sức quang trọng . Bởi vì xét cho cùng việc giáo
dục phải được tiến hành trên cơ sở nhận thức, tự hành động, việc khơi dậy phát truyển ý
thức năng lực tư duy bồi dưỡng năng lực tự học là con đường phát truyển tối ưu của giáo
dục.
Hiện nay có rất nhiều sách nâng cao và các tài liệu tham khảo, Internet,... song
chương trình bồi dưỡng của Huyện nhà chưa có sách hướng dẫn chi tiết, cụ thể từng tiết,
từng buổi học như trong chương trình chính khoá. Vì thế soạn thảo chương trình bồi
dưỡng là một việc làm hết sức quan trọng và rất khó khăn nếu như chúng ta không có sự
tham khảo, tìm tòi và chọn lọc tốt. Giáo viên cần soạn thảo nội dung bồi dưỡng dẫn dắt
học sinh từ cái cơ bản của nội dung chương trình học chính khoá, tiến dần tới chương
trình nâng cao (tức là trước hết phải khắc sâu kiến thức cơ bản của nội dung học chính
khoá, từ đó vận dụng để mở rộng và nâng cao dần).
Qua những năm giảng dạy bộ môn tại trường THCS Lương Thế Vinh , tôi cũng đã
thu được một số kết quả trong công tác ôn học sinh giỏi, đã có các học sinh đạt giải các
Sáng kiến kinh nghiệm môn vật lý năm học 2018 - 2019
Giáo viên: Lê Thị Hiệp – Trường THCS Lương Thế Vinh Trang 3
cấp. Ban thân nhận thấy qua các đề thi học sinh giỏi các cấp thì bài toán cực trị luôn xuất
hiện và nó thường là bài toán khó với học sinh
Với mong muốn công tác ôn luyện này đạt kết quả tốt, thường xuyên và khoa học
hơn, góp phần hoàn thành mục tiêu giáo dục, nâng cao chất lượng giáo dục của địa
phương, tôi chọn đề tài sáng kiến kinh nghiệm năm học này là: “Bồi dưỡng HSG với Các
bào toán cực trị trong vật lý ”.
2. Mục tiêu, nhiệm vụ của đề tài.
- Nghiên cứu các đề thi hoc sinh giỏi huyện, học sinh giỏi cấp tính, và thi vào các trường
chuyên
- Lựa chọn một số bài tập tính giá trị lớn nhất, giá trị nhỏ nhất ở các phần cơ học, điện
học, quang học.
- Tìm phương pháp giải và hướng dẫn học sinh giải bài tập tính giá trị lớn nhất, giá trị
nhỏ nhất ở các phần cơ học, điện học, quang học.
- Nghiên cưu qua quá trình nhận thức của học sinh và thời gian bồi dưỡng
3. Đối tượng nghiên cứu.
- Chương trình bồi dưỡng học sinh giỏi vật lý 9
- Đội tuyển học sinh giỏi vật lý 9 năm học 2017-2018
- Cách giải các bài toán tính giá trị lớn nhất, giá trị nhỏ nhất ở các phần cơ học, điện học,
quang học.
I.4. Giới hạn của đề tài.
- Các bài toán về cực trị của phần Cơ học, điện học, quang học.
- Đưa ra các chủ đề cần bồi dưỡng cho học sinh giỏi vật lý.
I.5. Phương pháp nghiên cứu.
- Thu thập thông tin qua sách, các đề thi, qua mạng internet.
- Phương pháp thử nghiệm.
- Phương pháp phân tích.
II. Phần nội dung
1. Cơ sở lý luận.
- Bài toán cực trị là một trong những dạng bài tập hay và khó trong quá trình bồi
dưỡng học sinh giỏi. Là một bài tập thường xuất hiện trong hầu hết các đề thi học
sinh giỏi tỉnh cũng như đề thi tuyển sinh vào trường chuyên lớp 10.
Sáng kiến kinh nghiệm môn vật lý năm học 2018 - 2019
Giáo viên: Lê Thị Hiệp – Trường THCS Lương Thế Vinh Trang 4
- Để giải được bài toán cực trị về điện học không những học sinh phải lập được biểu
thức mà cần phải áp dụng kiến thức toán học phù hợp để giải quyết
- Toán về cực trị thường chỉ có một số cách giải nhất định nhưng thuộc phần nâng
cao của môn toán nên nhiều học sinh thường chưa hiểu hay chưa từng được tiếp
xúc với dạng bài tập này.
2.Thực trạng vấn đề nghiên cứu.
a.Thuận lợi- khó khăn.
- Được sự chỉ đạo, quan tâm sâu sát và kịp thời của BGH, có những kế hoạch cụ
thể, lâu dài trong công việc bồi dưỡng HSG.
- Trường có cơ sở vật chất khá khang trang, trang thiết bị phục vụ tương đối đầy đủ
giúp cho việc dạy và học đạt kết quả tốt.
- Giáo viên có trình độ chuyên môn vững vàng, có nhiều kinh nghiệm trong công
tác bồi dưỡng HSG nhiều năm liền.
- Đa số học sinh chưa tiếp xúc với dạng bài tập này và chưa có kiến thưc toán để
giải và thế giáo viên cần phải dạy kiến thức toán trước khi áp dụng vào vật lý
- Đa số giáo viên dạy bồi dưỡng vừa phải bảo đảm chất lượng đại trà, vừa phải
hoàn thành chỉ tiêu chất lượng mũi nhọn và công tác kiêm nhiệm do đó cường độ làm
việc quá tải và việc đầu tư cho công tác bồi dưỡng HSG cũng có phần bị hạn chế. Vì thế
giáo viên bồi dưỡng thường chọn một số bài tập rồi hướng dẫn học sinh giải
- Học sinh học chương trình chính khóa phải học quá nhiều môn, cộng thêm
chương trình bồi dưỡng HSG nên rất hạn chế về thời gian tự học nên các em đầu tư ít thời
gian cho việc học bồi dưỡng HSG,
- Với kiến thức toán học còn hạn chế
b. Thành công - hạn chế.
- Đã đưa ra được một số phương pháp giải bài toán cực trị cho học sinh.
- Qua các năm khi học sinh tiếp xuc với bài tập cực trị cũng đã có hướng giải quyết
c. Mặt mạnh- mặt yếu.
- Có được đội ngũ học sinh giỏi ham học và ưu thích tìm hiểu tạo ra môi trường
học tập sôi động.
d. Các nguyên nhân, các yếu tố tác động.
3.Nội dung và hình thức các giải pháp
a. Mục tiêu của giải pháp.
Qua một thời gian tham gia công tác bồi dưỡng HSG, tôi nhận thấy để nâng cao
chất lượng trong công tác này cần thực hiện tốt những công việc sau đây:
- GV phải tự đặt ra mục tiêu về kiến thức kỹ năng cần rèn luyện cho đối tượng học
sinh mà mình đã lựa chọn,
- Lựa chọn hệ thống bài tập phù hợp với mục tiêu đó phân tích giải bài tập từ đó
đưa ra những khó khăn và sai lầm học sinh có thể mắc phải. Để đưa ra hệ thống câu hỏi
phù hợp
- Muốn có HSG phải có Thầy giỏi vì thế người thầy phải luôn luôn có ý thức tự
rèn luyện, tích lũy tri thức và kinh nghiệm, trau dồi chuyên môn, luôn xứng đáng là
Sáng kiến kinh nghiệm môn vật lý năm học 2018 - 2019
Giáo viên: Lê Thị Hiệp – Trường THCS Lương Thế Vinh Trang 5
“người dẫn đường tin cậy” cho học sinh noi theo. Phải thường xuyên tìm tòi các tư liệu,
có kiến thức nâng cao trên các phương tiện, đặc biệt là trên mạng internet. Lựa chọn trang
Web nào hữu ích nhất, tiện dụng nhất, tác giả nào hay có các chuyên đề hay, khả quan
nhất để sưu tầm tài liệu…
- Trong công tác BDHSG khâu đầu tiên là khâu tuyển chọn học sinh khâu này rất
quan trọng. Như phần trên tôi nói, đó là: Chúng ta lựa chọn đội tuyển ngay sau khi kết
thục năm học thông qua việc trao đổi với GV giảng dạy trước đó để lựa chọn những em
có khả năng, tư chất, trí tuệ, lòng đam mê vào đội tuyển, làm nguồn cho năm học kế tiếp.
- Đăc biệt biên soạn chương trình, nội dung bồi dưỡng rõ ràng, cụ thể, chi tiết cho
từng mảng kiến thức rèn luyện các kỹ năng ngôn ngữ theo số tiết quy định nhất định và
nhất thiết phải bồi dưỡng theo quy trình từ thấp đến cao, từ dễ đến khó để các em HS bắt
nhịp dần.
b. Nội dung và cách thức thực hiện giải pháp.
Một số bài tập trong đề thi học sinh giỏi cấp tỉnh đăk lăk trong những năm gần
đây:
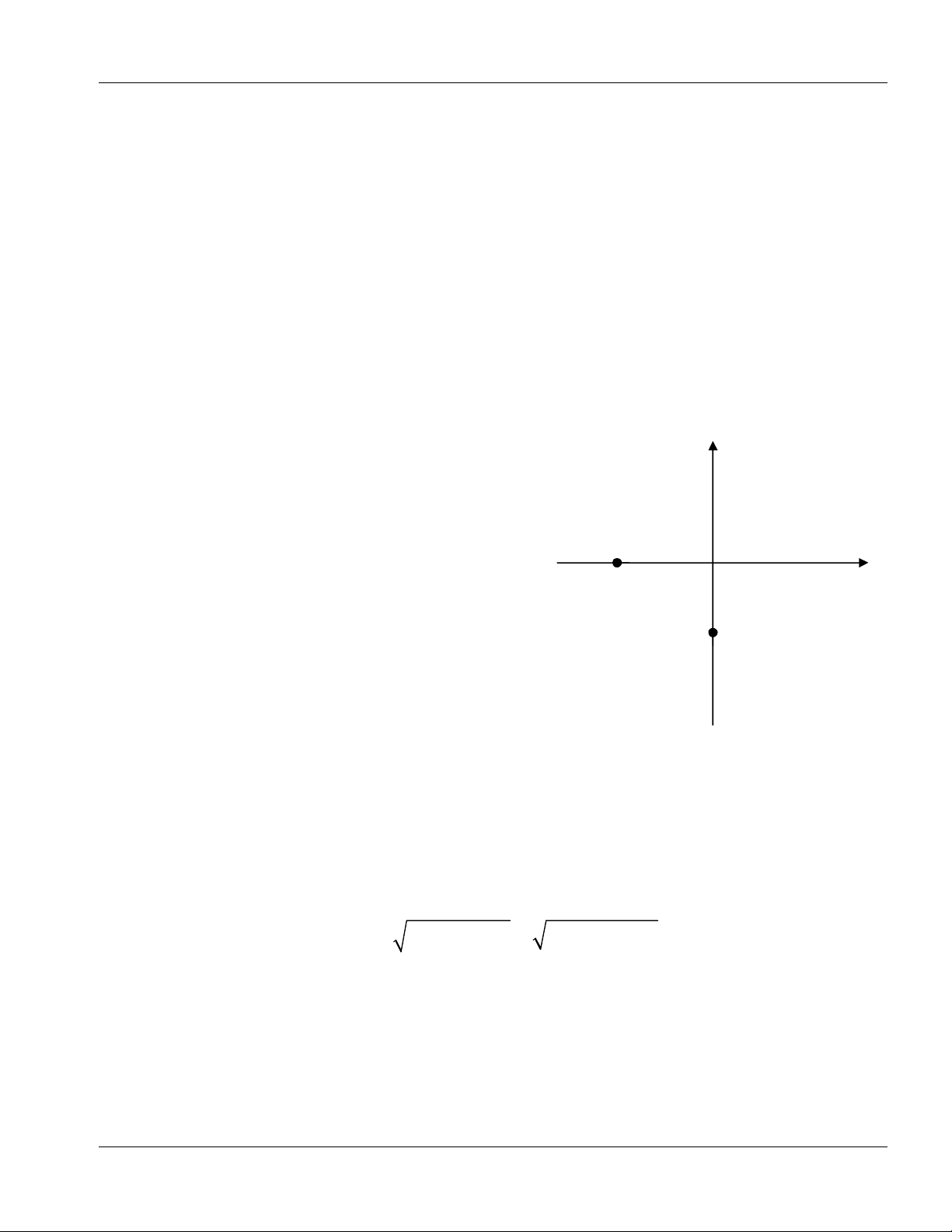
Bài 1 (HSG 2013) Hai Xe đạp đi theo hai
đường vuông góc, Xe A đi theo hướng từ
O đến x với tốc độ V1 = 25km/h; xe B đi
theo hướng từ O đến y với tốc độ v2 = 15km/h.
Luc 6 giờ hai xe cách giao điểm O của hai
đường là OA = 4,4km; OB = 4km, như hình
vẽ coi chuyển động thẳng đều.
1) Tính khoảng cách giữa hai xe tại thời điểm 6 giờ 15 phút .
2) Tính thời điểm mà khoản cách giữa hai xe là nhỏ nhất.
thời gian đi của mỗi xe là t = 6h15 phút - 6h00 = 15 phút = 0,25 h
quảng đường đi được của mỗi xe sau thời gian t là
s = v1.t = 25t = 25.0,25 = 6,25km
s2 = v2t = 15.0,25 = 3,75km
sau thời gian t xe 1 ở A1 xe 2 ở vị trí B1 như hình vẽ khoản cách giữa hai xe là L = A1B1
áp dụng định lý pytago ta có L =
2 2 2 2
1 2
OA OA 1,85 0,25
1,86km
tương tự khoản cách giữa hai xe sau thời gian t là
2 2 2
2 2
2 2
L (4,4 25t) (4 15t)
L 850t 340t 35,36
850t 340t 35,36 L 0
Để tồn tại giá trị của t thì phương trình * có nghiệm
A
B
O
x
y
