1
PHÒNG GDĐT VINH
TRƯỜNG THCS LÊ LỢI
SÁNG KIẾN KINH NGHIỆM
“HƯỚNG DẪN HỌC SINH KHAI THÁC CÓ HIỆU QUẢ
BÀI TOÁN VỀ BA ĐƯỜNG CAO TRONG TAM GIÁC”
Vinh, ngày 04 tháng 04 năm 2011
2
PHẦN I: ĐẶT VẤN ĐỀ
Học toán gắn liền với hoạt động giải toán. Thông qua việc hướng dẫn học
sinh giải toán, người giáo viên cần rèn luyện cho học sinh năng lực tư duy, tính
độc lập, linh hoạt, sáng tạo nhằm đáp ứng yêu cầu đào tạo con người mới. Việc
khai thác hiệu quả các bài toán là một trong những cách bồi dưỡng cho học sinh
những năng lực đó. Ngoài ra, việc khai thác có hiệu quả bài toán còn đem lại
cho học sinh những giờ học thú vị, lòng say mê hứng thú môn học, bởi tâm lý
học sinh nói chung luôn muốn biết và tìm tòi cái mới. Để rèn luyện kỹ năng giải
toán cho học sinh, một phương pháp hữu hiệu là từ một bài toán ban đầu và cách
giải bài toán đó, ta có thể hướng dẫn học sinh khai thác để phát biểu và giải
được nhiều bài toán khác.
Để khai thác và phát triển một bài toán, ta có thể sử dụng các cách sau:
- Sử dụng triệt để kết quả chứng minh được, lật ngược vấn đề và khai thác bài
toán đảo.
- Sử dụng kết quả bài toán và một số phép biển đổi hình học như đối xứng tâm,
đối xứng trục để tạo ra bài toán mới chứng minh được bằng cách sử dụng kết
quả bài toán đã có.
- Khái quát hoá đi đến bài toán tổng quát.
- Đặc biệt hoá để khai thác bài toán cực trị.
- Tương tự, mở rộng bài toán….
Việc hướng dẫn học sinh cách khai thác một bài toán là một trong những
vấn đề khó khăn đối với giáo viên, đòi hỏi người giáo viên cần phải có vốn kiến
thức sâu rộng, kiên trì và cần nhiều thời gian. Đối với học sinh, việc rèn luyện
kỹ năng khai thác là rất cần thiết, nhằm nâng cao khả năng tự học, sáng tạo, tư
duy độc lập và đặc biệt là gây được hứng thú học tập.
Qua thực tế giảng dạy, tôi nhận thấy rằng bài tập về đường tròn là rất quan
trọng đối với học sinh, đặc biệt là chương III hình học 9: “Góc với đường tròn”.
Mặt khác lượng kiến thức và bài tập về đường tròn tương đối nhiều và đa dạng
nên học sinh khá khó khăn trong việc hệ thống dạng bài tập cũng như cách giải.
Vì vậy, nếu từ một bài toán đơn giản ban đầu, nếu biết cách hướng học sinh tìm
3
lời giải rồi từ đó tạo ra được một số bài toán nhằm củng cố lại hệ thống kiến
thức đã học thì việc thu nhận và hệ thống kiến thức của chương trở nên dễ dàng
hơn đối với học sinh đại trà nói chung và phát triển tư duy cho học sinh khá giỏi
nói riêng.
Nhằm khắc phục những khó khăn trong việc hướng dẫn học sinh cách tự học
và cách khai thác bài toán có hiệu quả, tôi đã rút ra một số kinh nghiệm để củng
cố và phát triển tư duy cho học sinh. Trong đề tài này tôi xin trình bày việc
“Hướng dẫn học sinh khai thác có hiệu quả bài toán về ba đường
cao trong tam giác” để củng cố và nâng cao kiến thức chương III, Hình học
9 cho học sinh; đặc biệt là kỹ năng chứng minh tứ giác nội tiếp và khai thác các
tính chất của tứ giác nội tiếp để giải toán.
4
PHẦN II: NỘI DUNG
Ta bắt đầu từ bài tập 10 trang 104 - SGK Toán 9 - Tập Một.
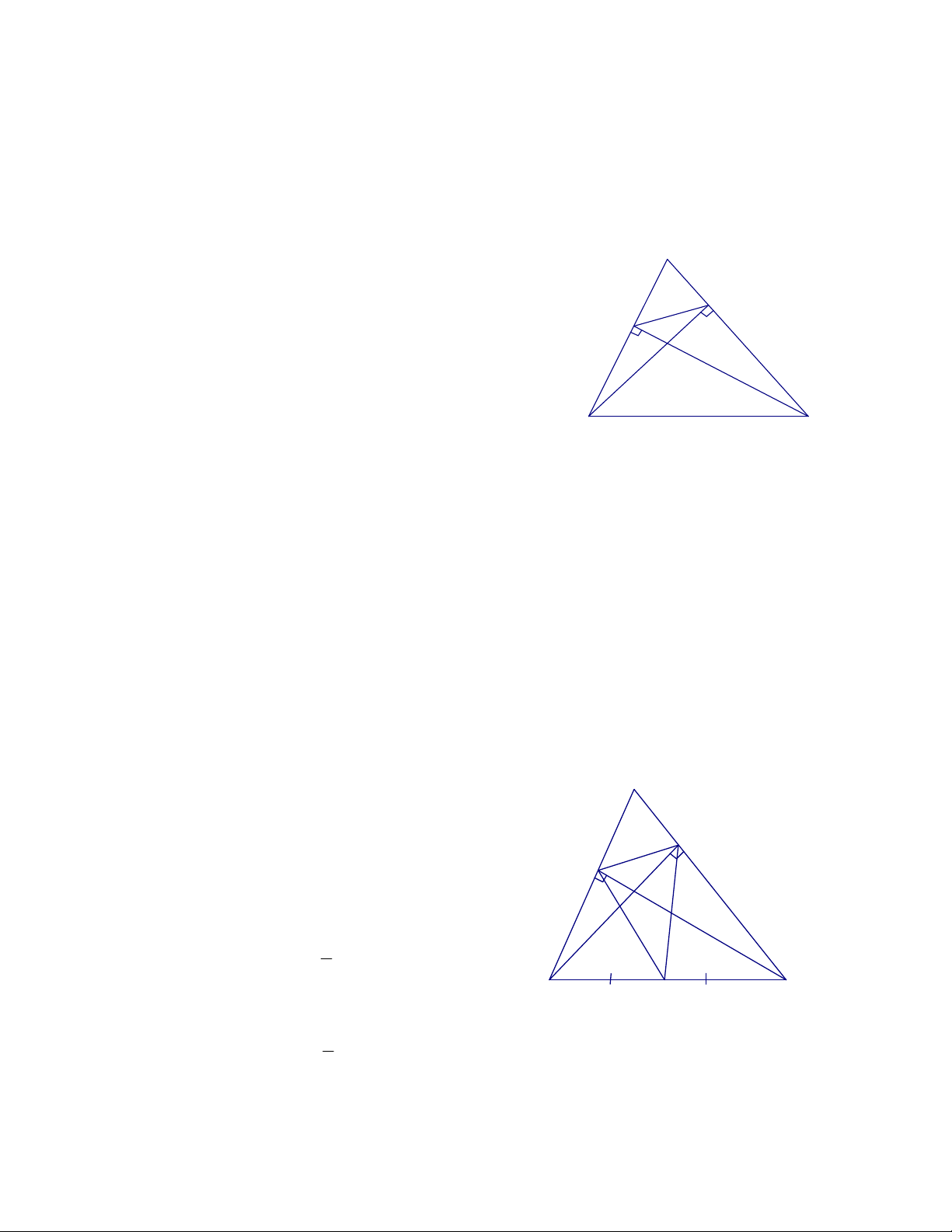
Bài toán 1: Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a. Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b. DE < BC.
Phân tích bài toán: Đây là bài toán thuộc
Chương II “Đường tròn” của chương trình Hình
học 9. Là bài tập nhằm củng cố lại định nghĩa
đường tròn và mối liên hệ giữa đường kính và
dây của đường tròn, nên để giải bài tập ta cần
chỉ rõ cho học sinh phương pháp. Cụ thể:
a) Để chứng minh 4 điểm B, E, C, D cùng thuộc một đường tròn ta có thể:
- Chỉ ra một điểm cách đều cả 4 điểm B, E, C, D (đó là trung điểm I của đoạn
BC) hoặc
- Chỉ ra có một đường tròn đi qua cả 4 điểm B, E, C, D là đường tròn đường
kính BC.
b) Từ kết quả chứng minh ở câu a) => ED và BC là hai dây của một đường
tròn và BC là đường kính của đường tròn đó => ED < BC (Định lí liên hệ giữa
dây và đường kính).
Từ đó ta có cách giải bài toán như sau:
Giải:
a) Cách 1:
Gọi I là trung điểm của đoạn BC.
∆ BEC vuông tại E (gt) => trung tuyến
EI = IB = IC =
1
2
BC
∆ BDC vuông tại D (gt) => trung tuyến
DI = IB = IC =
1
2
BC
A
BC
D
E
I
A
BC
D
E
5
Do đó IE = ID = IB = IC => 4 điểm B, C, D, E cùng thuộc một đường tròn,
đó là đường tròn tâm I, bán kính
1
2
BC.
Cách 2:
0
90
=> E
đường tròn đường kính BC
0
90
BDC
=> D
đường tròn đường kính BC
Do đó E, D thuộc đường tròn đường kính BC => 4 điểm B, E, D, C cùng
thuộc đường tròn đường kính BC.
b. Trong đường tròn đường kính BC: ED là dây, BC là đường kính
=> ED < BC (liên hệ giữa dây và đường kính trong một đường tròn).
* Nhận xét 1:
- Kết quả bài toán trên luôn đúng với mọi tam giác ABC.
- Nếu bài tập này được đưa ra sau bài “Tứ giác nội tiếp” của Chương III,
Hình học 9, ta có thể phát biểu kết quả câu a) dưới hình thức khác: Chứng
minh tứ giác BECD nội tiếp và dấu hiệu được sử dụng là hai đỉnh kề nhau
cùng nhìn cạnh chứa hai đỉnh còn lại dưới hai góc bằng nhau hoặc tứ giác
có 4 đỉnh cùng nằm trên một đường tròn. Từ bài toán này ta có thể khai thác
thành một số bài toán nhằm củng cố các kiến thức về góc với đường tròn và
phát triển tư duy cho học sinh. Cụ thể:
1. Đối với học sinh trung bình có thể cho học sinh nêu kết quả tương tự
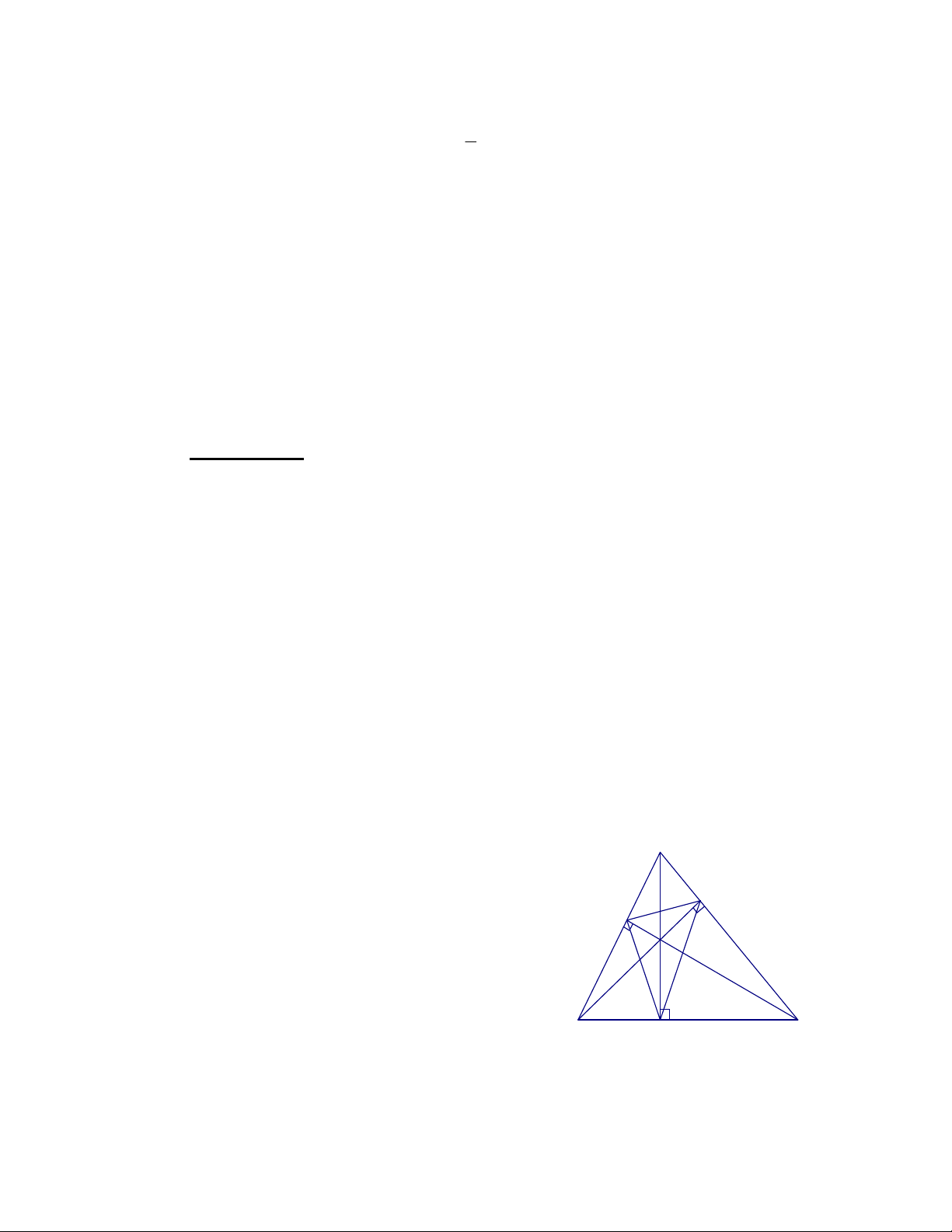
- Nếu gọi H là giao điểm của BD và CE => H là trực tâm của tam giác ABC
và AH
BC tại K.
Chứng minh tương tự ta có các kết quả sau:
a. Bốn điểm:
C, K, E, A cùng thuộc đường tròn đường
kính AC;
A, D, K, B cùng thuộc đường tròn đường
kính AB;
A, E, H, D cùng thuộc đường tròn đường kính AH;
C, D, H, K cùng thuộc đường tròn đường kính CH;
E
D
C
B
A
K
H