Taøi lieäu oân thi TN THPT. Naêm hoïc 2010 - 2011
* KHAÛO SAÙT VAØ VEÕ ÑOÀ THÒ HAØM SOÁ *
1. Khaûo saùt vaø veõ ñoà thò haøm soá:
SÔ ÑOÀ KHAÛO SAÙT HAØM SOÁ
Haøm soá baäc 3: y = f(x) = ax3 + bx2 + cx + d (a ≠ 0)
• Taäp xaùc ñònh: D = R
• y' = f'(x)
y' = 0: giaûi phöông trình y’ = 0
• y'' = f''(x)
y'' = 0: giaûi phöông trình y’’ = 0.
Keát luaän ñieåm uoán I.
• Giôùi haïn:
y
x−∞→
lim
=
y
x+ ∞→
lim
=
• Baûng bieán thieân:
Keát luaän s ự ñoàng bieán, nghòch bieán c a hàm sủ ố.
Keát luaän caùc ñieåm cöïc trò cuûa ñoà thò haøm soá.
• Ñieåm ñaëc bieät:
Giao ñieåm vôùi truïc tung: x = 0 tìm y.
Giao ñieåm vôùi truïc hoaønh: y = 0 giaûi phöông trình f(x) = 0 tìm x.
• Ñoà thò: ñoà thò haøm soá nhaän ñieåm uoán I laøm taâm ñoái xöùng.
Haøm soá baäc 4 truøng phöông y = f(x) = ax4 + bx2 + c (a ≠ 0):
• Taäp xaùc ñònh: D = R
• y' = f'(x)
y' = 0: giaûi phöông trình y’ = 0
• Giôùi haïn:
y
x−∞→
lim
=
y
x+ ∞→
lim
=
• Baûng bieán thieân.
Keát luaän s ự ñoàng bieán, nghòch bieán c a hàm sủ ố.
Keát luaän caùc ñieåm cöïc trò cuûa ñoà thò haøm soá.
• Ñieåm ñaëc bieät:
Giao ñieåm vôùi truïc tung: x = 0 tìm y.
Giao ñieåm vôùi truïc hoaønh (neáu coù): y = 0 giaûi phöông trình f(x) = 0 tìm x.
• Ñoà thò: ñoà thò haøm soá nhaän truïc tung laøm truïc ñoái xöùng.
Haøm soá höõu tyû daïng y = f(x) =
dcx
bax
+
+
(ad – cb ≠ 0, c ≠ 0):
• Taäp xaùc ñònh: D = R\{
c
d
−
}
• y' = f'(x)
Keát luaän s ự ñoàng bieán, nghòch bieán c a hàm sủ ố.
• Giôùi haïn:
y
x−∞→
lim
=
c
a
,
y
x+ ∞→
lim
=
c
a
⇒ Tieäm caän ngang y =
c
a
y
xx
+
→
0
lim
=
=
−
→
y
xx
0
lim
⇒ Tieäm caän ñöùng x = x
0
• Baûng bieán thieân:
Keát luaän haøm soá khoâng coù cöïc trò.
• Ñieåm ñaëc bieät:
Giao ñieåm vôùi truïc tung: x = 0 tìm y.
Giao ñieåm vôùi truïc hoaønh: y = 0 giaûi phöông trình f(x) = 0 tìm x.
----- Taøi lieäu löu haønh noäi boä ----- 1
Taøi lieäu oân thi TN THPT. Naêm hoïc 2010 - 2011
• Ñoà thò: ñoà thò haøm soá nhaän giao ñieåm hai ñöôøng tieäm caän laøm taâm ñoái xöùng.
Baøi taäp reøn luyeän:
Baøi 1: Khaûo saùt vaø veõ ñoà thò caùc haøm soá:
a) y = x
3 + 3x2 - 4; b) y = -x3 - 3x2 + 1; c) y = -x3 +
3x2 - 4x + 2;
d) y = x3 - 3x2 + 4x + 1; e) y =
3
3
x
- x2 + x + 1; f) y = -
3
3
x
+ x2
- x + 1.
Baøi 2 : Khaûo saùt vaø veõ ñoà thò caùc haøm soá:
a) y = x
4 - 2x2 - 3; b) y = -x4 + 2x2 +1; c) y = -
2
4
x
- x2 +
2
3
; d) y
=
2
4
x
+ x2 +
2
3
.
Baøi 3 : Khaûo saùt vaø veõ ñoà thò caùc haøm soá:
a) y =
;b) y =
12
2
+
−
x
x
; c) y =
x
x1
+
; d) y =
x
1
.
Baøi taäp töï luyeän:
Baøi 1: Khaûo saùt vaø veõ ñoà thò caùc haøm soá:
a) y = x
3 - 6x2 + 9x; b) y = x3 + 1; c) y =
3
1
x3 - x2 - 3x -
3
5
;
d) y = -x3 + 3x2 - 3x - 1; e) y = 2x3 - 3x2 - 2; f) y = x3 - x2 + x.
Baøi 2: Khaûo saùt vaø veõ ñoà thò caùc haøm soá:
a) y =
24
2
3
4
1xx −
; b) y =
2
3
x
2
x
2
4
−+
; c) y = -
24
x
2
3
x
4
1
+
; d) y =
24
2
3
4
1xx
−−
.
Baøi 3: Khaûo saùt vaø veõ ñoà thò caùc haøm soá:
a) y =
7
23
+
−
x
x
; b) y =
x
x
−
−
1
2
; c) y =
23
12
+
−
x
x
;
d) y =
12
2
−
−
x
x
; e) y =
2
2x 3
−+
; f) y =
1
−
x
x
.
2. Phöông trình tieáp tuyeán cuûa ñoà thò haøm soá:
* Daïng 1: Tieáp tuyeán cuûa ñoà thò haøm soá y = f(x) taïi ñieåm M(x
0; y0) naèm treân ñoà thò
haøm soá:
y – y 0 = f’(x0)(x – x0)
ª Cho hoaønh ñoä tieáp ñieåm x
0: tính tung ñoä tieáp ñieåm y0 = f(x0).
ª Cho tung ñoä tieáp ñieåm y0: giaûi phöông trình f(x) = y0, tìm hoaønh ñoä tieáp
ñieåm.
* Daïng 2: Tieáp tuyeán cuûa ñoà thò haøm soá y = f(x) bieát heä soá goùc cho
tröôùc:
Goïi M(x0; y0) laø toïa ñoä tieáp ñieåm ⇒ heä soá goùc tieáp tuyeán laø f’(x0).
ª Bieát heä soá goùc tieáp tuyeán laø soá k: giaûi phöông trình f’(x0) = k, tìm x0.
ª Bieát tieáp tuyeán vuoâng goùc vôùi d: y = k1x + m1: giaûi phöông trình k1.f’(x0)
= -1, tìm x0.
ª Bieát tieáp tuyeán song song vôùi ∆: y = k2x + m2: giaûi phöông trình f’(x0) = k2,
tìm x0.
Baøi taäp reøn luyeän:
Baøi 1: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y = x
3 - 3x2 + 4 taïi ñieåm M(0; 4).
----- Taøi lieäu löu haønh noäi boä -----
2
Taøi lieäu oân thi TN THPT. Naêm hoïc 2010 - 2011
Baøi 2: Cho haøm soá y = x
2 coù ñoà thò (C), vieát phöông trình tieáp tuyeán cuûa ñoà
thò (C) taïi ñieåm coù tung ñoä baèng 4.
Baøi 3: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y = x3 - 3x2 + 4 taïi
ñieåm coù hoaønh ñoä baèng 2.
Baøi 4: Cho haøm soá
2 x
yx 1
−
=+
(1). Vieát phöông trình tieáp tuyeán vôùi ñoà thò (C)
cuûa haøm soá (1) taïi giao ñieåm cuûa ñoà thò (C) vôùi caùc truïc toïa ñoä.
Baøi 5: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá
3
y x 3x
= − +
bieát
tieáp tuyeán ñoù coù heä soá goùc k = -9.
Baøi 6: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y = x3 - 5x2 + 2 bieát
raèng tieáp tuyeán naøy song song vôùi ñöôøng thaúng y = -3x + 1.
Baøi 7: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y = x3 - 5x2 + 2
bieát raèng tieáp tuyeán naøy vuoâng goùc vôùi ñöôøng thaúng y =
7
1
x - 4.
Baøi taäp töï luyeän:
Baøi 1: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y =
1
32
+
+
x
x
taïi ñieåm coù hoaønh ñoä x0
= -3 thuoäc ñoà thò haøm soá.
Baøi 2: Cho haøm soá y = x2 - 1 coù ñoà thò (C), vieát phöông trình tieáp tuyeán cuûa ñoà
thò (C) taïi ñieåm coù tung ñoä baèng 8.
Baøi 3: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y = x3 - 5x2 + 2 bieát raèng tieáp
tuyeán naøy song song vôùi ñöôøng thaúng y = -3x + 1.
Baøi 4: Vieát phöông trình tieáp tuyeán cuûa ñoà thò haøm soá y = x3 - 5x2 + 2 bieát raèng tieáp
tuyeán naøy vuoâng goùc vôùi ñöôøng thaúng y =
7
1
x - 4.
Baøi 5: Cho haøm soá y =
1
12
+
−
x
x
coù ñoà thò (C). Vieát phöông trình tieáp tuyeán cuûa (C):
a) Taïi giao ñieåm cuûa (C) vôùi truïc tung.
b) Taïi ñieåm coù hoaønh ñoä
0
x
= – 2.
c) Bieát tieáp tuyeán coù heä soá goùc
3
1
.
d) Bieát tieáp tuyeán vuoâng goùc vôùi ñöôøng thaúng x + 3y = 0.
Baøi 6: Cho haøm soá y = x
4 - 2x2 + 1 coù ñoà thò (C). Vieát phöông trình tieáp tuyeán
vôùi ñoà thò (C) taïi ñieåm cöïc ñaïi cuûa (C).
3. Giao ñieåm cuûa hai ñöôøng - Bieän luaän soá nghieäm cuûa phöông trình baèng ñoà thò:
a) Tìm toïa ñoä giao ñieåm cuûa hai ñöôøng cong:
Giaû söû haøm soá y = f(x) coù ñoà thò (C
1) vaø haøm soá y = g(x) coù ñoà thò laø (C2).
Giaûi phöông trình hoaønh ñoä giao ñieåm f(x) = g(x).
b) Bieän luaän soá nghieäm phöông trình f(x) = g(m)(*) vôùi g(m) laø ñöôøng
thaúng cuøng phöông Ox:
Soá nghieäm phöông trình (*) baèng soá giao ñieåm cuûa hai ñöôøng (C): y = f(x)
vaø d: y = g(m).
Baøi taäp reøn luyeän:
Baøi 1: Tìm toïa ñoä giao ñieåm cuûa ñoà thò hai haøm soá:
a) (C): y = x
2 - 2x + 2 vaø d: y = x; b) (C): y = x3 + 4x2 + 4x + 1 vaø
d: y = x + 1;
c) (C): y = x3 - 3x vaø d: y = x2 + x - 4; d) (C): y = x4 - 4x2 + 5 vaø d: y =
x2 + 1.
Baøi 2: Döïa vaøo ñoà thò (C) cuûa haøm soá y = -x3 + 3x2 - 1 bieän luaän theo m
soá nghieäm phöông trình:
----- Taøi lieäu löu haønh noäi boä ----- 3
Taøi lieäu oân thi TN THPT. Naêm hoïc 2010 - 2011
a) -x
3 + 3x2 - 1 = m; b) x3 - 3x2 + 1 + m = 0; c) -x3 + 3x2 - 2 = m.
Baøi 3: Döïa vaøo ñoà thò (C) cuûa haøm soá y = x4 - 2x2 + 3 bieän luaän theo m
soá nghieäm phöông trình:
a)
2
1
x4 - x2 +
2
3
= m; b) 2x4 - 4x2 + 6 + m = 0; c) 2x4 - 4x2 + 4
- m = 0.
Baøi taäp töï luyeän:
Baøi 1: Bieän luaän soá nghieäm phöông trình x
2 + 2x + 1 + m = 0 theo hai phöông phaùp
(duøng bieät thöùc ∆ vaø phöông phaùp bieän luaän baèng ñoà thò)
Baøi 2: Döïa vaøo ñoà thò cuûa haøm soá y = x3 + 3x2, haõy bieän luaän soá
nghieäm cuûa phöông trình x3 + 3x2 + m = 0 tuøy theo giaù trò cuûa tham soá m.
Baøi 3: Cho haøm soá y =
1
23
−
−
x
x
. Tìm taát caû caùc giaù trò cuûa tham soá m ñeå
ñöôøng thaúng y = mx + 2 caét ñoà thò cuûa haøm soá ñaõ cho taïi hai ñieåm phaân
bieät.
Baøi 4: Bieän luaän theo m soá giao ñieåm cuûa hai ñöôøng:
a) (C): y = x
3 - 4x2 + 4x vaø d: y = m + 1; b) (C): y =
2
2
−
+
x
x
vaø d: y =
m - 2.
4. Tìm giaù trò lôùn nhaát (GTLN), giaù trò nhoû nhaát (GTNN) cuûa haøm soá:
a) Giaù trò lôùn nhaát (GTLN), giaù trò nhoû nhaát (GTNN) cuûa haøm soá y = f(x) treân ñoaïn [a; b]:
• Tìm x
i ∈ (a; b) (i = 1, 2, ..., n) maø taïi ñoù f'(xi) = 0 hoaëc f'(xi) khoâng xaùc
ñònh.
• Tính f(a), f(b), f(xi) (i = 1, 2, ..., n).
• Keát luaän
)(max
);(
xf
ba
= max[f(a), f(xi), f(b)] (i = 1, 2, ..., n)
)(min
);(
xf
ba
= min[f(a), f(xi), f(b)] (i = 1, 2, ..., n).
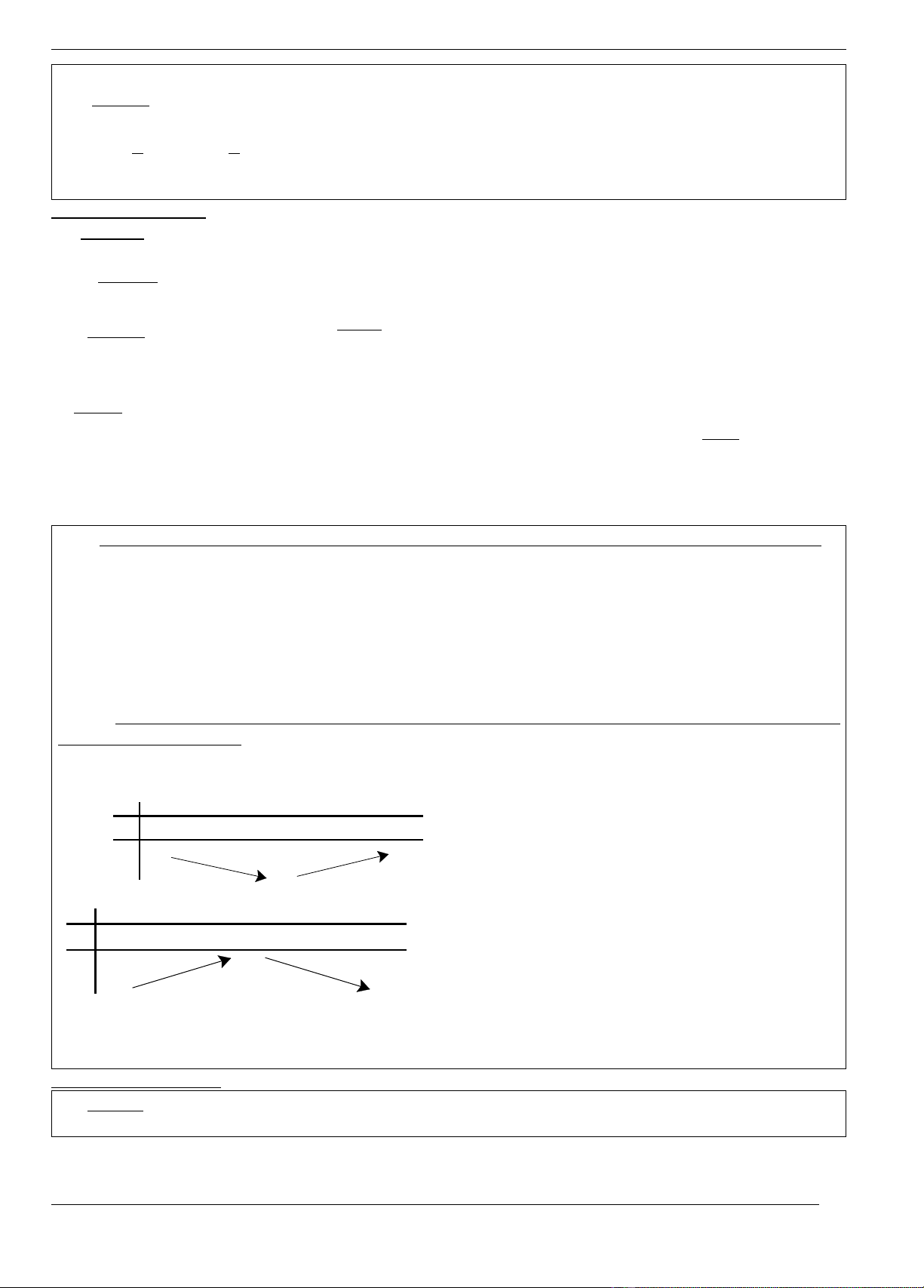
b) Giaù trò lôùn nhaát (GTLN), giaù trò nhoû nhaát (GTNN) cuûa haøm soá y = f(x)
treân khoaûng (a; b):
Cho haøm soá y = f(x) lieân tuïc treân khoaûng (a; b) (a,b coù theå laø -∞, +∞),
ta coù hai tröôøng hôïp:
GTNN
f(
x
0
)
+
-
limy
x
→
b
x
→
a
limy
0
x
0
b
a
y
y'
x
GTLN
f(
x
0
)
+
-
limy
x
→
b
x
→
a
limy
0
x
0
b
a
y
y'
x
(Trong ñoù y'(x 0) baèng 0 hoaëc y'(x) khoâng xaùc ñònh taïi x0).
Keát luaän:
)(max
);(
xf
ba
= f(x
0) taïi x = x0 hoaëc
)(min
);(
xf
ba
= f(x0) taïi x = x0.
Baøi taäp reøn luyeän:
Baøi 1: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá y = x3 - 3x2 - 9x
+ 35 treân ñoaïn [-4; 2].
----- Taøi lieäu löu haønh noäi boä -----
4
Taøi lieäu oân thi TN THPT. Naêm hoïc 2010 - 2011
Baøi 2: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá
lny x x
= −
treân
ñoaïn
1;
2e
� �
� �
� �
.
Baøi 3: Tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá f(x) = x - e2x
treân ñoaïn [-1; 0].
Baøi 4: Tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá f(x) = x +
2
4x−
.
Baøi 5: Tìm giaù trò lôùn nhaát, nhoû nhaát cuûa haøm soá y = cos
3x - 6cos2x + 9cosx + 5.
Baøi 6 : Tìm giaù trò lôùn nhaát, nhoû nhaát cuûa caùc haøm soá sau:
a) y =
2
4x
x
+
treân khoaûng (-∞; +∞); b) y = x +
x
4
vôùi x > 0.
Baøi taäp töï luyeän:
Baøi 1: Tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá f(x) = x
4 - 2x2 + 1 treân
ñoaïn [0; 2].
Baøi 2: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá y =
x36
−
treân
ñoaïn [-1; 1].
Baøi 3: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá f(x) = sin2x - x
treân ñoaïn [-
2
;
2
ππ
].
Baøi 4: Tím caùc giaù trò lôùn nhaát, nhoû nhaát cuûa caùc haøm soá sau:
a) f(x) =
x45
−
treân ñoaïn [-1; 1]; b) f(x) = 1 +
2
9x
−
treân ñoaïn [-3; 3];
c) f(x) =
2
+
x
x
treân [-2; 4]; d) f(x) = x2 - 3x + 2 treân ñoaïn [-10;
10].
Baøi 5: Tím caùc giaù trò lôùn nhaát, nhoû nhaát cuûa caùc haøm soá sau:
a) y =
2
cos2x + 4sinx treân ñoaïn [0;
2
π
]. b) f(x) = sin4x -
4sin2x + 5.
Baøi 6: Tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa caùc haøm soá:
a)
22
( ) x x
f x e
−
=
treân
[ ]
0;3
; b)
x
xexf 2)(
=
treân [-3; 1]; c)
( ) .
−
=
x
f x x e
treân
[ ]
0;2
.
Baøi 7: Tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa caùc haøm soá:
a)
)ln( exy
+=
treân [0; e]; b)
xxy ln.
2
=
treân
[ ]
e;1
.
Baøi 8: Tìm caùc giaù trò lôùn nhaát, nhoû nhaát cuûa caùc haøm soá sau:
a) y = 1 + 5x - 3x2; b) y = 3x2 - 4x + 7; c) y =
x
x2
2
+
(x > 0);
d) y = 4x3 - 3x4; e) y = x + 2 +
1
1
−x
treân khoaûng (1; +∞).
5. Ñònh tham soá ñeå haøm soá ñaït cöïc trò taïi x0:
Neáu haøm soá y = f(x) ñaït cöïc trò taïi x
0 thì f'(x0) = 0.
Baøi taäp reøn luyeän:
Baøi 1: Ñònh m ñeå haøm soá y = -(m
2 + 5m)x3 + 6mx2 + 6x - 5 ñaït cöïc ñaïi taïi x = 1.
Baøi 2: Tìm caùc giaù trò cuûa m ñeå x = 1 laø ñieåm cöïc tieåu cuûa haøm soá y =
1
1
2
+
−+−
x
mmxx
.
Baøi taäp töï luyeän:
----- Taøi lieäu löu haønh noäi boä ----- 5