
265
THIẾT KẾ RUBRICS ĐÁNH GIÁ NĂNG LỰC
MÔ HÌNH HÓA TOÁN HỌC CỦA HỌC SINH TRONG DẠY HỌC
CHỦ ĐỀ ỨNG DỤNG CỦA CỰC TRỊ HÀM SỐ
Ngô Hùng Vương1
1. Khoa Sư phạm, Trường Đại học Thủ Dầu Một
TÓM TẮT
Bài báo cáo đề xuất xây dựng thang đánh giá năng lực mô hình hóa toán học của học
sinh trong dạy học chủ đề “ứng dụng của cực trị hàm số” lớp 12 dựa trên các biểu hiện và yêu
cầu cần đạt của năng lực mô hình hóa ở cấp trung học phổ thông theo chương trnh giáo dục
phổ thông môn toán năm 2018. Đồng thời nghiên cứu cũng thiết kế rubrics đánh giá chi tiết
năng lực mô hình hóa toán học của người học thông qua một bài tp thực tế gắn liền với ứng
dụng của cực trị hàm số.
Từ khóa: cực trị hàm số, năng lực mô hình hóa toán học, rubric.
1. ĐẶT VẤN ĐỀ
Những năm gần đây giáo dục phổ thông ở Việt Nam đang có những thay đổi lớn, chuyển
nền giáo dục nặng về truyền thụ kiến thức sang nền giáo dục phát triển toàn diện cả về phẩm
chất và năng lực. Đồng thời, cách đánh giá kết quả giáo dục cũng phải đáp ứng được yêu cầu
chuyển đổi từ đánh giá khả năng ghi nhớ của học sinh sang kiểm tra – đánh giá phẩm chất, năng
lực vận dụng kiến thức, giải quyết vấn đề; kết hợp kiểm tra – đánh giá kết quả học tập với kiểm
tra – đánh giá trong quá trình học tập để có thể tác động kịp thời đến việc DH. Từ đó nâng cao
chất lượng hoạt động dạy học ở nhà trường.
Theo Chương trình giáo dục phổ thông môn Toán 2018, (Thông tư 32 của Bộ Giáo dục
và Đào tạo), giáo dục toán học cần hình thành và phát triển cho học sinh những phẩm chất chủ
yếu, năng lực chung và năng lực toán học. Và mô hình hóa toán học (MHHTH) là một trong
năm thành tố cốt lõi của năng lực toán học. Năng lực MHHTH giúp học sinh biết liên kết, vận
dụng được những kiến thức toán học vào các môn học khác (Vật lý, Hóa học,…) đồng thời giải
quyết được các vấn đề thực tế trong cuộc sống hàng ngày. Tuy nhiên làm thế nào để xác định
một cách chính xác các mức độ đạt được năng lực này ở học sinh là một câu hỏi được đặt ra.
Xuất phát từ câu hỏi thực tế trên, bài viết đ thiết kế thang đánh giá năng lực MHHTH
của học sinh dựa trên tiêu chí và các mức độ cần đạt của từng tiêu chí, đồng thời minh họa chi
tiết thang đánh giá này thông qua dạy học nội dung “ứng dụng của cực trị hàm số”. Qua đó giúp
giáo viên dễ dàng hơn trong việc đánh giá năng lực MHHTH của học sinh.

266
2. PHƯƠNG PHÁP NGHIÊN CỨU
Bài viết chủ yếu sử dụng phương pháp phân tích và tổng hợp tài liệu. Trên cơ sở phân
tích và tổng hợp lý thuyết về năng lực MHHTH, các công cụ đánh giá, từ đó đề xuất thiết kế
rubrics đánh giá năng lực MHHTH của người học thông qua một bài tập thực tế gắn liền với
chủ đề ứng dụng của cực trị hàm số.
3. KẾT QUẢ VÀ THẢO LUẬN
3.1. Quan điểm về năng lực mô hình hóa toán học
3.1.1. Mô hình hóa toán học
MHHTH là quá trình chuyển đổi một vấn đề thực tế sang một vấn đề toán học bằng cách
thiết lập và giải quyết các mô hình toán học, kiểm tra và đánh giá lại lời giải trong ngữ cảnh thực
tế, cải tiến mô hình nếu cách giải quyết chưa phù hợp (Blum và nnk., 2007). Hay nói một các
ngắn gọn MHHTH là quá trình giải quyết những vấn đề thực tế bằng công cụ toán (Trần Vui,
2014).
Tóm lại MHHTH là quá trình sử dụng mô hình toán học (công thức, phương trình, bảng
biểu, đồ thị) để giải quyết vấn đề. Nó là quá trình chuyển đổi từ vấn đề thực tế sang vấn đề Toán
học, sau đó đối sánh, điều chỉnh và chuyển ngược lại. Quá trình này là một vòng lặp và chỉ
dừng lại khi thu được kết quả hợp lý.
Từ quan điểm về MHHTH của Swetz và Hartzler (1999); Blum và LeiB (2006), có thể
chia quá trình MHHTH thành 4 bước như sau như sau:
• Bước 1: Chuyển hóa tình huống thực tiễn thành tình huống Toán học;
• Bước 2: Thiết lập mô hình toán học phù hợp với vấn đề toán học vừa xây dựng được;
• Bước 3: Sử dụng công cụ toán học để giải quyết mô hình toán học;
• Bước 4: Đối chiếu, kiểm tra lại kết quả đạt được trong điều kiện thực tế và điều chỉnh
lại mô hình cho phù hợp với yêu cầu đặt ra của tình huống nếu kết quả chưa hợp lí.
3.1.2. Năng lực mô hình hóa toán học
Có rất nhiều định nghĩa và quan điểm khác nhau về năng lực MHHTH được chia sẻ bởi
những nhà nghiên cứu giáo dục. Maab (2006) định nghĩa NL MHHTH bao gồm các kĩ năng và
khả năng thực hiện quá trình MHH nhằm đạt được mục tiêu xác định cũng như sẵn sàng đưa ra
những hành động. Blomhoj và Jensen (2007), cũng có quan điểm gần giống Maab, cho rằng
năng lực MHHTH là khả năng thực hiện đầy đủ các giai đoạn của quá trình MHHTH trong một
tình huống cho trước. Như vậy, có thể hiểu năng lực MHHTH là khả năng thực hiện được toàn
bộ quá trình MHHTH để giải quyết một vấn đề thực tiễn.
Với những quan niệm về năng lực MHHTH như trên, các nhà nghiên cứu đ dựa vào các
bước của quá trình MHHTH để xác định các năng lực thành phần của năng lực MHHTH, đó là:
- Hiểu vấn đề thực tế và chuyển sang vấn đề toán học;
- Biết thiết lập mô hình toán học từ vấn đề toán học;

267
- Biết giải quyết được những vấn đề toán học trong mô hình được thiết lập;
- Kiểm tra, đánh giá được lời giải trong ngữ cảnh thực tế và cải tiến được mô hình nếu
cách giải quyết không phù hợp .
3.2. Khái niệm rubric trong kiểm tra – đánh giá.
Rubric là một bản hướng dẫn chấm điểm được sử dụng để đánh giá kết quả học tập của
học sinh. Rubric thường chứa các tiêu chí đánh giá, các cấp độ và thang điểm cụ thể của từng
tiêu chí (Popham và James ,1997) đồng thời thường được trình bày dưới dạng bảng. Rubric có
thể được sử dụng bởi giáo viên khi chấm điểm và bởi học sinh khi lập kế hoạch làm bài (Dawson
và Phillip, 2015).
Heidi Goodrich (2000) định nghĩa rubric là một công cụ dùng để cho điểm bằng cách liệt
kê tất cả các tiêu chí đánh giá bài học, bài tập, bài làm hay công việc mà người học thực hiện
bằng cách xếp loại theo thứ bậc.
Nói cách khác, rubric là một bảng mô tả chi tiết, rõ ràng các tiêu chuẩn, tiêu chí và các
mức độ mà học sinh có thể đạt được khi thực hiện các nhiệm vụ học tập như thuyết trình, làm
việc nhóm, bài tập, bài kiểm tra. Các tiêu chuẩn, tiêu chí được xây dựng dựa trên nội dung và
mục tiêu của các hoạt động học tập. Sử dụng rubrics giúp việc chấm điểm của giáo viên đơn
giản và khách quan hơn còn học sinh sẽ dễ dàng tự đánh giá và lên kế hoạch học tập.
Một rubric được đánh giá là chất lượng nếu thỏa các tiêu chí trong bảng 1.
Bảng 1. Bảng tiêu chí đánh giá chất lượng của một rubric
Phạm trù đánh giá
Các tiêu chí đánh giá phản ánh đầy đủ nội dung, mục tiêu học
tập không?
Mức độ
Phân chia các mức độ và giá trị điểm số tương ứng có phù hợp
không?
Tiêu chí
Các thông tin có mô tả rõ ràng, thể hiện theo một chuỗi liên
kết và đảm bảo cho sự phát triển của học sinh không?
Thân thiện với học sinh
Ngôn ngữ có rõ ràng, dễ hiểu đối với học sinh không?
Thân thiện với giáo viên
Có dễ sử dụng với giáo viên không?
Tính phù hợp
Có thể đánh giá kết quả học tập được không?
Từ các tiêu chí trên có thể thấy một rubric có chất lượng nếu: Các tiêu chí đánh giá được
mô tả trong rubric phải phản ánh được đầy đủ nội dung, mục tiêu học tập. Đồng thời, việc phân
chia các mức độ và giá trị điểm số tương ứng của mỗi tiêu chí đánh giá phải phù hợp, các thông
tin ở từng mức độ đánh giá cần được mô tả một cách rõ ràng, thể hiện theo một chuỗi liên kết,
đảm bảo cho sự phát triển của học sinh. Bên cạnh đó, phải xt xem ngôn ngữ được sử dụng trong
rubric có rõ ràng, dễ dàng sử dụng đối với giáo viên và cả học sinh hay không. Cuối cùng, thang
tiêu chí đánh giá phải có tính phù hợp, có thể dùng để đánh giá được kết quả học tập của học sinh.
3.3. Xây dựng rubric đánh giá năng lực MHHTH gắn với chủ đề “ứng dụng của cực
trị hàm số” ở lớp 12
• Yêu cầu cần đạt đối với năng lực MHHTH cấp trung học phổ thông
Chương trình giáo dục phổ thông môn Toán 2018 mô tả biểu hiện cụ thể và yêu cầu cần
đạt của năng lực MHHTH ở cấp trung học phổ thông như sau:

268
Bảng 2. Biểu hiện cụ thể và yêu cầu cần đạt của năng lực MHHTH
ở cấp trung học phổ thông
Biểu hiện của năng lực MHHTH
Yêu cầu cần đạt
– Xác định được MHH Toán học (gồm công thức,
phương trình, bảng biểu, đồ thị,…) cho tình huống
xuất hiện trong bài toán thực tiễn.
– Giải quyết được những vấn đề Toán học trong
mô hình được thiết lập.
– Thể hiện và đánh giá được lời giải trong ngữ
cảnh thực tế và cải tiến được mô hình nếu cách giải
quyết không phù hợp.
– Thiết lập được mô hình toán học (gồm công thức,
phương trình, sơ đồ, hình vẽ, bảng biểu, đồ thị,…) để
mô tả tình huống đặt ra trong một số bài toán thực tiễn.
– Giải quyết được những vấn đề toán học trong mô
hình được thiết lập.
– Lí giải được tính đúng đắn của lời giải (những kết
luận thu được từ các tính toán là có ý nghĩa, phù hợp
với thực tiễn hay không). Đặc biệt, nhận biết được
cách đơn
giản hoá, cách điều chỉnh những yêu cầu thực tiễn (xấp
xỉ, bổ sung thêm giả thiết, tổng quát hoá,…) để đưa
đến những bài toán giải được.
• Đặc trưng của quá trình mô hình hóa bài toán thực tế gắn với chủ đề “ứng dụng của
cực trị hàm số” ở lớp 12.
Các bài toán thực tế gắn với chủ đề “ứng dụng của cực trị hàm số” thường yêu cầu xác
định giá trị nhỏ nhất hoặc giá trị nhỏ nhất của hàm số, nghĩa là phải tính được đạo hàm của hàm
số, mà như ta đ biết để tính được đạo hàm thì phải thiết lập được hàm số (ở đây là hàm số một
biến). Như vậy ta có thể mô tả quá trình MHHTH cho một bài toán thực tế gắn với chủ đề “ứng
dụng của cực trị hàm số” như sau
Bước 1: Đơn giản hóa bài toán. Xác định được yếu tố cần tìm, yếu tố đ cho, mối quan
giữa chúng rồi biểu diễn chúng dưới dạng biến số, tìm các điều kiện tồn tại của chúng cũng như
sự ràng buộc.
Bước 2: Dựa vào các kiến thức liên quan đến vấn đề thực tế như trong đời sống kinh tế,
trong khoa học kỹ thuật như Vật Lý, Hóa học, Sinh học,…mà thiết lập được hàm số phụ thuộc
vào một biến số (mô hình toán học).
Bước 3: Sử dụng đạo hàm của hàm số một biến để khảo sát và tìm cực trị của hàm số.
Bước 4: Kiểm tra và giải thích ý nghĩa của kết quả thu được.
Từ mô tả quá trình MHHTH cho một bài toán thực tế gắn với chủ đề “ứng dụng của cực
trị hàm số”, dựa vào Bảng 2 nêu trên và các rubric đánh giá đã tham khảo, bài viết đề xuất trong
Bảng 3 dưới đây một rubric đánh giá năng lực MHHTH.
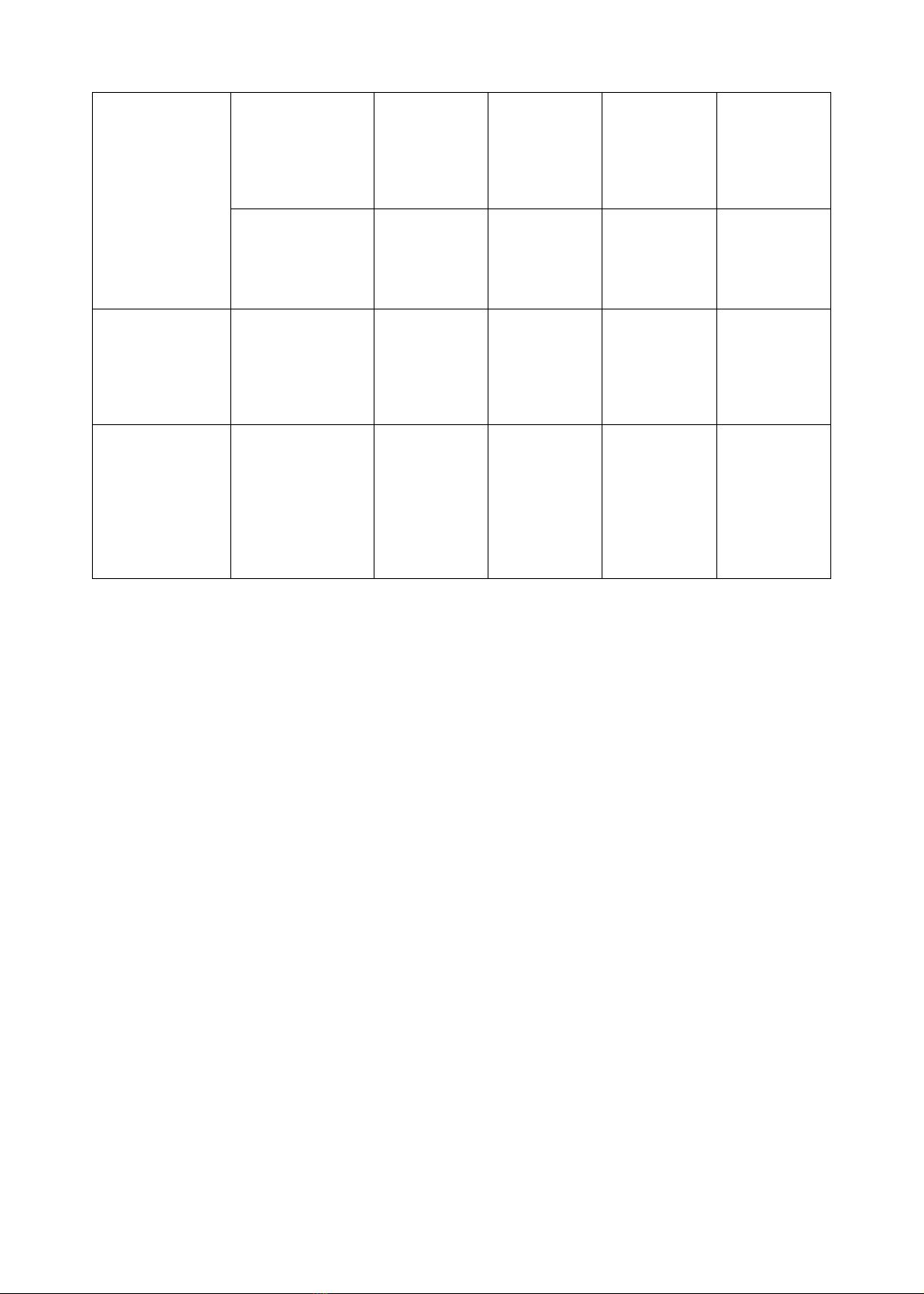
Bảng 3. Rubric đánh giá năng lực MHHTH gắn với chủ đề “ứng dụng của cực trị hàm số”
ở lớp 12.
Tiêu chuẩn
(Năng lực thành
phần)
Tiêu chí
Mức
Cần cố gắng
Trung bình
Khá
Tốt
1. Thiết lập được
mô hình toán học
mô tả bài toán
thực tiễn
1.1. Xác định biến,
tham số, hằng số
(kèm theo điều
kiện ràng buộc)
Không xác
định được
biến
Xác định được
biến nhưng
thiếu điều
kiện
Xác định được
biến và điều
kiện
Xác định được
biến , điều
kiện và giải
thích được vì
sao có điều
kiện đó
269
1.2. Thiết lập các
mệnh đề toán học
(thiết lập được
quan hệ giữa yếu
tố đ cho và yếu tố
cần tìm)
Không thiết
lập được các
mệnh đề toán
học
Thiết lập được
một vài mệnh
đề toán học
Thiết lập được
khá đầy đủ
các mệnh đề
toán học
Thiết lập được
đầy đủ các
mệnh đề toán
học
1.3. Thiết lập được
hàm số một biến
Không giải
thích và
không thiết
lập được hàm
số một biến
Giải thích
được nhưng
không thiết
lập được hàm
số một biến
Giải thích và
thiết lập được
hàm số nhưng
chưa đúng
một biến
Giải thích và
thiết lập đúng
hàm số một
biến
2. Giải quyết
được những vấn
đề toán học trong
mô hình được
thiết lập
2.1. Vận dụng đạo
hàm của hàm số
một biến để tìm
cực trị nó.
Không lấy
được đạo hàm
của hàm số
một biến
Lấy được đạo
hàm, nhưng
tìm sai cực trị
Lấy được đạo
hàm và tìm
đúng cực trị
Lấy được đạo
hàm, tìm đúng
cực trị, kiểm
tra được kết
quả là đúng
hay sai
3. Thể hiện và
đánh giá được lời
giải trong ngữ
cảnh thực tế và
cải tiến được mô
hình nếu cách giải
quyết không phù
hợp.
3.1. Lí giải được
tính đúng đắn của
lời giải
Không lý giải
được tính
đúng đắn của
kết quả tìm
được
Lý giải được
tính đúng đắn
của kết quả
tìm được
Lý giải được
tính đúng đắn
và giải thích
được ý nghĩa
của kết quả
tìm được
cải tiến được
mô hình nếu
cách giải
quyết không
phù hợp hoặc
khái quát hóa
được bài toán
thực tiễn
Rubric trên đ mô tả một thang đánh giá theo bốn mức độ: Tốt, khá, trung bình và cần
cố gắng. Đồng thời thực hiện đánh giá 3 NL thành phần là “Thiết lập được mô hình toán học
mô tả bài toán thực tiễn”; “Giải quyết được những vấn đề toán học trong mô hình được thiết
lập” và “Thể hiện và đánh giá được lời giải trong ngữ cảnh thực tế và cải tiến được mô hình
nếu cách giải quyết không phù hợp” dựa trên các biểu hiện của năng lực MHHTH ở cấp trung
học phổ thông do bộ giáo dục và đào tạo đề ra.
• Minh họa Rubric đánh giá năng lực MHHTH trong dạy học chủ đề “ứng dụng cực trị
hàm số” lớp 12
Cho bài toán thực tế sau: Doanh nghiệp tư nhân Dũng Tiến chuyên kinh doanh các loại
xe gắn máy và tay ga của hãng Honda. Hiện nay, doanh nghiệp đang tập trung chiến lược vào
kinh doanh xe tay ga Air Blade với chi phí mua vào là 30 (triệu đồng) và bán ra với giá 45 (triệu
đồng) một chiếc. Với giá bán này thì doanh nghiệp tính toán được rằng số lượng xe bán ra là
2000 xe. Tuy nhiên với mong muốn đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang bán chạy
này, doanh nghiệp dự định sẽ giảm giá bán và ước tính rằng nếu giảm 1 (triệu đồng) mỗi chiếc
thì số lượng xe bán ra sẽ tăng thêm 800. Vậy doanh nghiệp phải đưa ra giá bán mới của mỗi
chiếc xe là bao nhiêu để việc giảm giá bán đem về lợi nhuận cao nhất?
Dựa vào Bảng 3 ở trên, thiết kế một rubric đánh giá năng lực MHHTH cho bài toán thực
tế trên như sau
























