Học Excel -
Thủ Thuật Excel
Xử lý các hàm lượng giác trong Excel
Danh mục và cách xử lý các hàm lượng giác trong Excel :
ACOS (number) : Trả về một giá trị radian nằm trong khoảng từ 0 đến Pi, là
arccosine, hay nghịch đảo cosine của một số nằm trong khoảng từ -1 đến 1
ACOSH (number) : Trả về một giá trị radian, là nghịch đảo cosine-hyperbol của
một số lớn hơn hoặc bằng 1
ASIN (number) : Trả về một giá trị radian nằm trong đoạn từ -Pi/2 đến Pi/2, là
arcsine, hay nghịch đảo sine của một số nằm trong khoảng từ -1 đến 1
ASINH (number) : Trả về một giá trị radian, là nghịch đảo sine-hyperbol của một
số
ATAN (number) : Trả về một giá trị radian nằm trong khoảng từ -Pi/2 đến Pi/2, là
arctang, hay nghịch đảo tang của một số
ATAN2 (x_num, y_num) : Trả về một giá trị radian nằm trong khoảng (nhưng
không bao gồm) từ -Pi đến Pi, là arctang, hay nghịch đảo tang của một điểm có tọa
độ x và y
ATANH (number) : Trả về một giá trị radian, là nghịch đảo tang-hyperbol của một
số nằm trong khoảng từ -1 đến 1
COS (number) : Trả về một giá trị radian, là cosine của một số
COSH (number) : Trả về một giá trị radian, là cosine-hyperbol của một số
DEGREES (angle) : Chuyển đổi số đo của một góc từ radian sang độ
RADIANS (angle) : Chuyển đổi số đo của một góc từ độ sang radian
SIN (number) : Trả về một giá trị radian là sine của một số
SINH (number) : Trả về một giá trị radian, là sine-hyperbol của một số
TAN (number) : Trả về một giá trị radian, là tang của một số
TANH (number) : Trả về một giá trị radian, là tang-hyperbol của một số
Hàm DEGREES()
Chuyển đổi số đo của một góc từ radian sang độ (1 radian = Pi/1800)
Cú pháp: = DEGREES(angle)
angle : là số đo góc tính theo radian
Ví dụ:
Hàm SIN()
Trả về một giá trị radian là sine của một số
Cú pháp: = SIN(number)
number : là số đo góc, tính theo radian
Lưu ý:
Nếu bạn muốn tính SIN() của một góc tính theo độ, hãy nhân nó với PI()/180, hoặc
sử dụng RADIANS() để chuyển nó từ độ sang radian
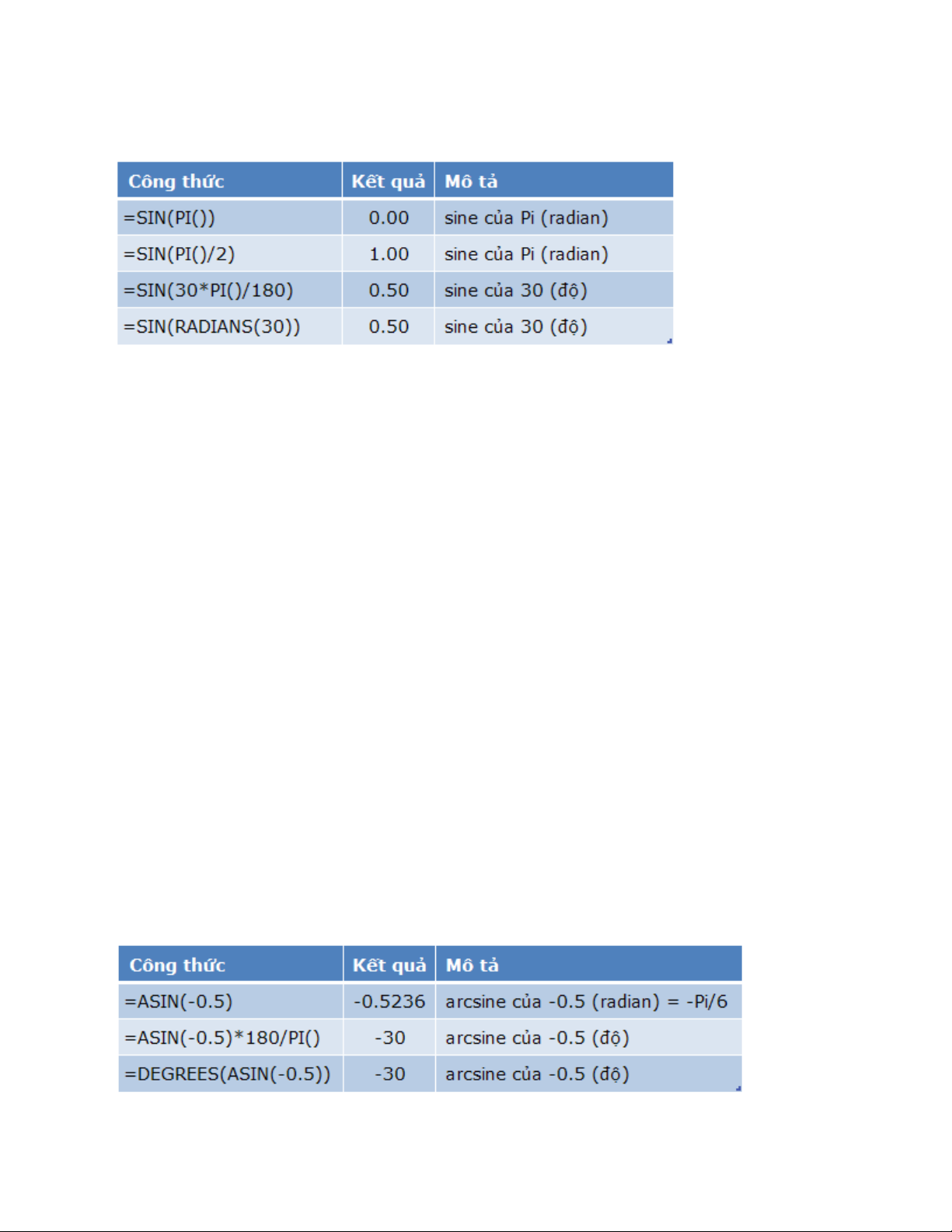
Ví dụ:
Hàm ASIN()
Trả về một giá trị radian nằm trong đoạn từ -Pi/2 đến Pi/2, là arcsine, hay nghịch
đảo sine của một số nằm trong khoảng từ -1 đến 1
Cú pháp: = ASIN(number)
number : Là sine của một góc và phải nằm trong khoảng từ -1 đến 1
Lưu ý:
· Nghịch đảo sine của một number là một giá trị mà sine của nó thì bằng number,
hay ASIN(SIN(number)) = number
· Nếu muốn chuyển đổi kết quả từ radian thành độ, bạn nhân kết quả với 180/PI()
hoặc sử dụng hàm DEGREES() để chuyển kết quả ra độ
Ví dụ:
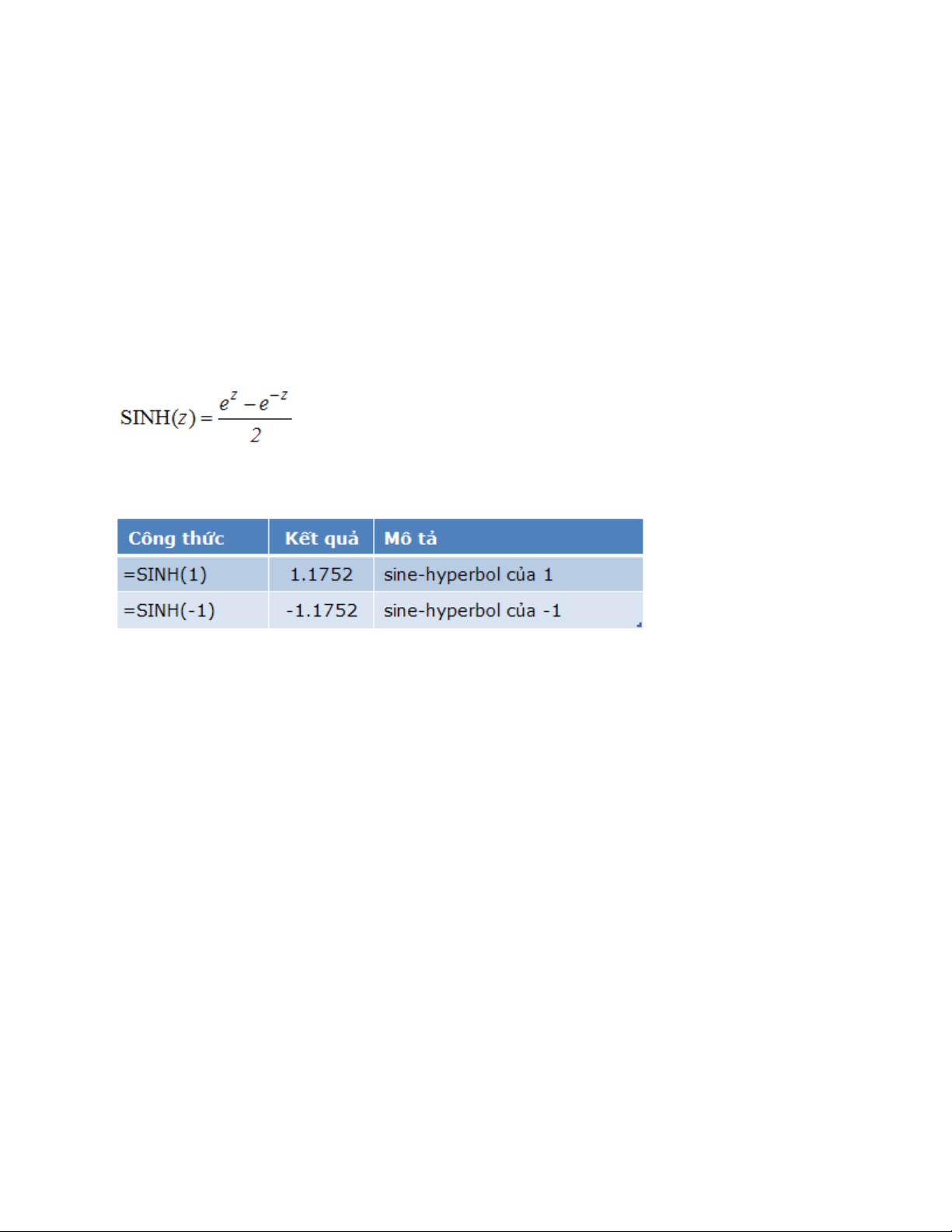
Hàm SINH()
Trả về một giá trị radian, là sine-hyperbol của một số.
Cú pháp: = SINH(number)
number : Là một số thực bất kỳ
Ghi chú:
Sine-hyperbol của một số được tính theo công thức:
Ví dụ:
Hàm ASINH()
Trả về một giá trị radian, là nghịch đảo sine-hyperbol của một số
Cú pháp: = ASINH(number)
number : Là một số thực bất kỳ
Lưu ý:
Nghịch đảo sine-hyperbol của một number là một giá trị mà sine-hyperbol của nó
thì bằng number, hay ASINH(SINH(number)) = number
Ví dụ: